本文主要是介绍运动规划_碰撞检测算法之分离轴定理,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
运动规划:碰撞检测算法之分离轴定理

附赠自动驾驶全套学习资料和量产经验:链接
如上文所述,基于包围形的方法是一种粗略的碰撞检测方法,基于外接圆形的方法运算速度很快,但精度很差;基于轴对齐包围矩形(AABB)的方法适合本身就是矩形的物体,其运算速度非常快,但检测精度还是不够。

1、OBB
OBB 就是找一个最小的包围物体的矩形,这在自动驾驶系统中也是最常用的,感知模块给出物体的轮廓通常就是此形状。另外,为了准确描述物体轮廓,感知模块在 bounding box 的基础上,通常还会给出 polygon(多边形)的形式,如下图所示。

2、向量的点乘
向量法判断点与线段的关系(一)
向量法判断点与线段的关系(二)
在介绍分离轴定理之前,还需要先理解向量点乘的数学定义和几何意义,如下图所示,若 a 向量为单位向量,则向量 a 和向量 b 的点乘可以理解为 b 向量投影到 a 向量上的长度。

有了上述背景知识,接下来我们介绍一种适用于 bounding box 和 polygon 的精细碰撞检测算法:分离轴定理(Separating Axis Theorem,SAT)。
3、分离轴定理
分离轴定理的理论依据为超平面分离定理,即 令 A 和 B 是两个不相交的非空凸集,那么存在一个非零向量 v 和 实数 c,使得 <x, v> ≤ c 且 <y, v> ≥ c。其中,x 属于 A,y 属于 B。
简单来说,就是对于两个凸多边形,若存在一条直线将两者分开,则这两个多边形不相交。

上图中的黑线为分离线(Seperating line),与之垂直的绿线为分离轴(Separating axis),图中虚线表示的是多边形在分离轴上的投影。
实际应用中,遍历所有角度的分离轴是不现实的,受益于多边形的性质,对于两个都是多边形的物体,只需要依次在每条边的垂直线做投影即可,如下图所示。

对于两个都是矩形的物体,则更简单,只需要做四次投影。

以下图中的两个多边形 A 和 B 为例,分离轴定理的具体步骤为:
-
首先根据边1的两个顶点位置坐标,计算出边1的向量,设为(x,y);
-
进而求出边1的法向量,作为分离轴,为(y, -x)或(-y,x)。若需要求两个多边形的最小分离距离,这里的法向量还需要化为单位向量;若只需判断两个多边形是否相交,则不需要化为单位向量;
-
依次将多边形 A 和 B 的所有顶点与原点组成的向量投影到这个分离轴上,并记录两个多边形顶点投影到分离轴上的最小值和最大值(Pmin,Pmax),形成一个投影线段;
-
判断这两个投影线段是否发生重叠,若不重叠,则有 (PAmax < PBmin)||(PAmin > PBmax);
-
若两个投影线段不重叠,则代表存在这样一条直线将两个多边形分开,两个多边形不相交,可以直接退出循环;
-
若两个投影线段重叠,则回到步骤1,继续以边2的法向量作为分离轴,进行投影计算;
-
当两个多边形的所有边都检查完之后,找不到这样一条分离的直线,则意味着两个多边形相交。

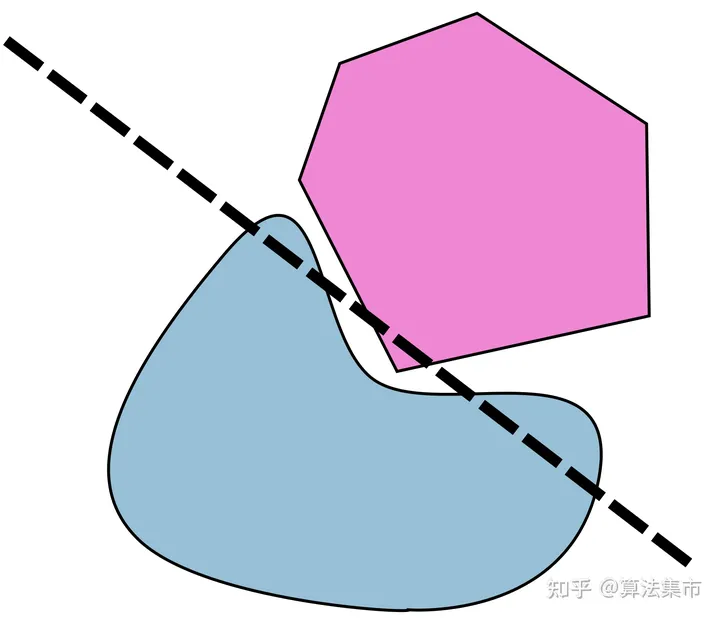
注意:分离轴定理是一种适用于凸多边形的碰撞检测算法,对于凹多边形则不适用,如下图所示,两个多边形没有碰撞,但找不到这样一条直线,能将两者分开。所以如果是凹多边形的话,需要先将其转换成多个凸多边形。
综上,分离轴定理是一种适用于 bounding box 和 polygon 的精细碰撞检测算法,其优点是算法原理简单,可准确判断两个多边形是否相交;缺点在于当多边形的边数较多时,该算法的效率较低(当两个多边形相交时,需要遍历完所有边进行判断)。
在实际应用中,为了提高效率,通常先使用 基于轴对齐包围矩形(AABB)的方法进行粗略的碰撞检测,然后再使用 分离轴定理(SAT)做精细碰撞检测。
这篇关于运动规划_碰撞检测算法之分离轴定理的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









