本文主要是介绍代码随想录算法训练营Day55 ||leetCode 583. 两个字符串的删除操作 || 72. 编辑距离,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
583. 两个字符串的删除操作
这道题的状态方程比上一题简单一些

初始化如下

class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1));for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;for (int i = 1; i <= word1.size(); i++) {for (int j = 1; j <= word2.size(); j++) {if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];} else {dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);}}}return dp[word1.size()][word2.size()];}
};72. 编辑距离
首先确认状态方程
如果第i位与第j位相同,那本次可以不用操作,dp[i][j]=dp[i-1][j-1]
如果不同,则需要增删改的操作,而增和删本质是等效的,对一个字符串删等于对另一个字符串加,所以取dp[i-1][j]和dp[i][j-1]的最小值+1。改的话则是dp[i-1][j-1]+1;取他们的最小值。
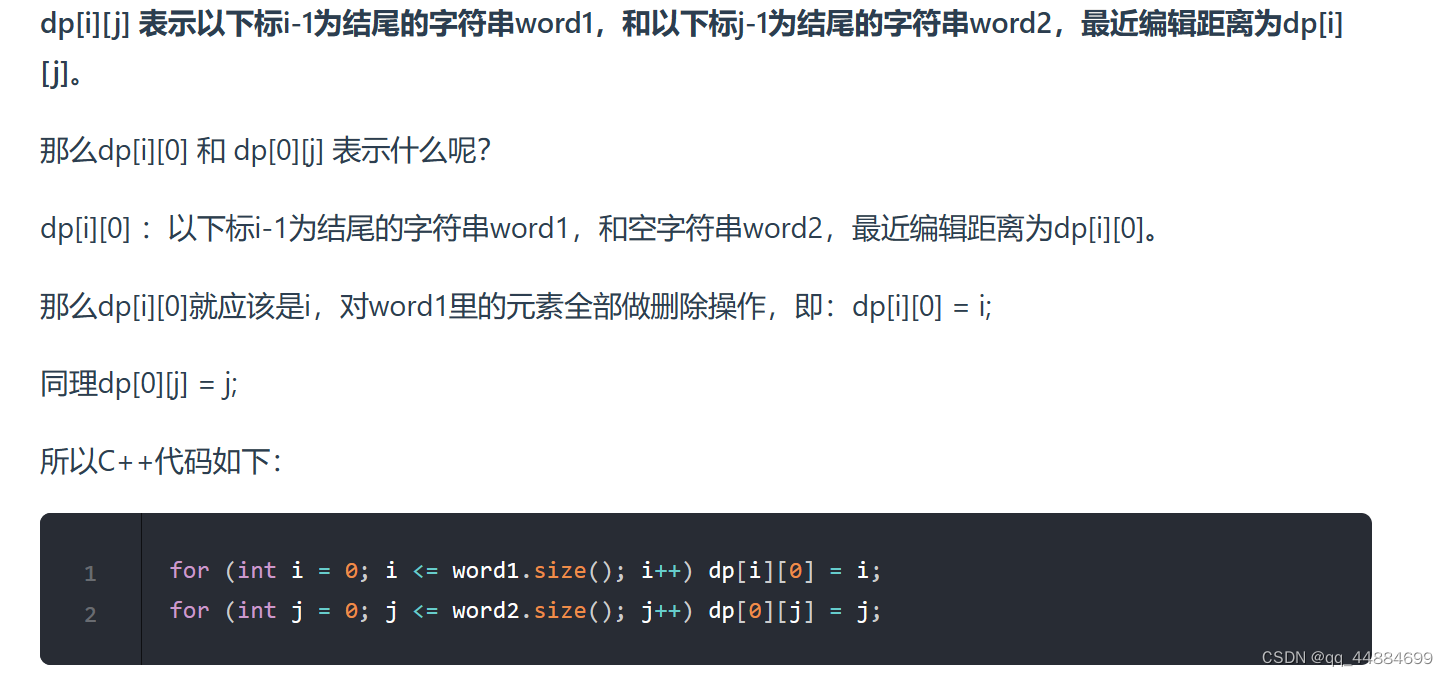
初始化则为
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;for (int i = 1; i <= word1.size(); i++) {for (int j = 1; j <= word2.size(); j++) {if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];}else {dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;}}}return dp[word1.size()][word2.size()];}
};这篇关于代码随想录算法训练营Day55 ||leetCode 583. 两个字符串的删除操作 || 72. 编辑距离的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




