采用蒙特卡洛树搜索实现3人斗地主AI

蒙特卡洛树搜索

全称 Monte Carlo Tree Search（MCTS），是一种人工智能问题中做出最优决策的方法，一般是在组合博弈中的行动（move）规划形式。它结合了随机模拟的一般性和树搜索的准确性。MCTS 受到快速关注主要是由计算机围棋程序的成功以及其潜在的在众多难题上的应用所致。超越博弈游戏本身，MCTS 理论上可以被用在以 {状态 state，行动 action} 对定义和用模拟进行预测输出结果的任何领域。

大数定律

MCTS的数学理论依据是大数定律，学习MCTS首先就要了解“大数定律”。

大数定律，说明了一些随机事件的均值的长期稳定性。人们发现，在重复试验中，随着试验次数的增加，事件发生的频率趋于一个稳定值；人们同时也发现，在对物理量的测量实践中，测定值的算术平均也具有稳定性。比如，我们向上抛一枚硬币，硬币落下后哪一面朝上是偶然的，但当我们上抛硬币的次数足够多后，达到上万次甚至几十万几百万次以后，我们就会发现，硬币每一面向上的次数约占总次数的二分之一，亦即偶然之中包含着必然。

MCTS通过很多次模拟真实对局，当模拟的次数足够多，（利用大数定律）模拟后获得的最佳收益的节点，就接近于理论上真实的最佳收益节点。那么这个节点所包含的Action（行动）就是当前state（状态）下最佳的选择。以斗地主来为例，MCTS就是在当前各家手牌的情况下，在符合斗地主规则和出牌常规的情况下框定可选的行动，进行n次模拟对局，每次对局都执行不完全相同的行动，记录和更新每种行动带来的收益，最终选择收益最佳的行动（出牌、跟牌或不出）。

一般情况下MCTS适用于二人零和完全信息博弈游戏。然而斗地主是3人游戏，并且是非完全信息博弈游戏，MCTS能适用吗？

我们先来尝试简化这个问题。首先，如果斗地主是明牌的，在规则允许的情况下，每个玩家的可选行动对其他玩家都是透明的，那就变成了3人完全信息博弈游戏。其次，斗地主中3个人分为两派，可以将2个农民和1地主之间的博弈，看成2人零和游戏。这样来考虑之后，斗地主就变成了MCTS擅长的“二人零和完全信息博弈游戏”了，理论上应该是可以实现的。

MCTS循环

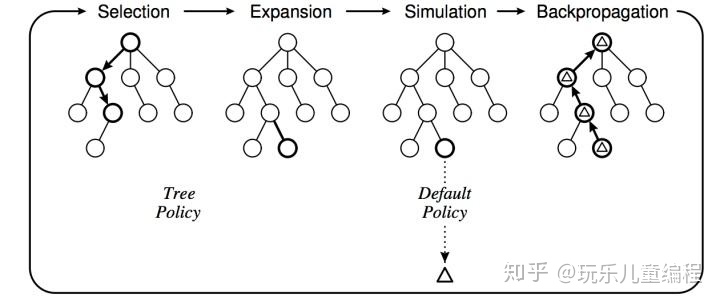
每一次MCTS树搜索分为4个步骤：

1.选择ÿ