本文主要是介绍网络分析(蓝桥杯,acwing,并查集),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目描述:
小明正在做一个网络实验。
他设置了 n 台电脑,称为节点,用于收发和存储数据。
初始时,所有节点都是独立的,不存在任何连接。
小明可以通过网线将两个节点连接起来,连接后两个节点就可以互相通信了。
两个节点如果存在网线连接,称为相邻。
小明有时会测试当时的网络,他会在某个节点发送一条信息,信息会发送到每个相邻的节点,之后这些节点又会转发到自己相邻的节点,直到所有直接或间接相邻的节点都收到了信息。
所有发送和接收的节点都会将信息存储下来。
一条信息只存储一次。
给出小明连接和测试的过程,请计算出每个节点存储信息的大小。
输入格式:
输入的第一行包含两个整数 n,m,分别表示节点数量和操作数量。
节点从 1 至 n 编号。
接下来 m 行,每行三个整数,表示一个操作。
- 如果操作为
1 a b,表示将节点 a 和节点 b 通过网线连接起来。当 a = b 时,表示连接了一个自环,对网络没有实质影响。 - 如果操作为
2 p t,表示在节点 p 上发送一条大小为 t 的信息。
输出格式:
输出一行,包含 n 个整数,相邻整数之间用一个空格分割,依次表示进行完上述操作后节点 1 至节点 n 上存储信息的大小。
数据范围:
1≤n≤10000
1≤m≤1e5
1≤t≤100
输入样例1:
4 8
1 1 2
2 1 10
2 3 5
1 4 1
2 2 2
1 1 2
1 2 4
2 2 1
输出样例1:
13 13 5 3分析步骤:
第一:这道题目是要确定哪些电脑是连接到了一起,哪些电脑是在同一个集合之中,所以应该运用并查集,将其要连接的合并;我们要计算到底储存了多少的信息,其实只要看这个点和根节点的距离到底有多少,如果是根节点的话则直接输出他的值,否则应该输出自身的值加上根节点的值
第二:书写主函数,构建整体框架:
将值输入,并查集数组更新自身,将自己设为自己的根节点。
进行判断如果操作是1的话则,去查找a , b 的父节点,如果a的父节点 != b的父节点 那么就将 d[a] 的值减去d[b]的值。它的作用是在合并操作中更新节点 a 的距离。由于在并查集合并时,将集合 a 合并到集合 b 中,所以要更新集合 a 中所有节点的距离,使其相对于根节点的距离保持一致。因此,这行代码的目的是将集合 a 中的每个节点的距离减去集合 b 的距离,以实现更新。这样,在输出结果时才能得到正确的距离信息。最后将a的父节点改为b。
进行判断如果操作是2的话则,去将a的集合根节点加上b。
用for循环判断如果是根节点则直接输出他的值,否则则输出自身的值加上根节点的距离
int main()
{scanf("%d%d", &n, &m); // 读取节点数和操作数for (int i = 1; i <= n; i ++ ) p[i] = i; // 初始化并查集的父节点为自身while (m -- ){int t, a, b;scanf("%d%d%d", &t, &a, &b); // 读取操作类型和操作数if (t == 1){a = find(a), b = find(b); // 查找a和b所属的集合的根节点if (a != b) // 如果a和b不在同一个集合中{d[a] -= d[b]; // 更新a的距离p[a] = b; // 将a所属的集合合并到b所属的集合中}}else{a = find(a); // 查找a所属的集合的根节点d[a] += b; // 更新a所属集合中的所有节点的距离(距离增加b)}}for (int i = 1; i <= n; i ++ )if ( i == find(i) ) printf("%d ", d[i]); // 输出根节点的距离else printf("%d ", d[i] + d[find(i)]); // 输出非根节点的距离(距离需要累加)puts("");return 0;
}
第四:书写find函数
判断x点的父节点是否是自身,不是的话就不断的向上递归去找寻真正的根节点(也就是最祖宗的那个节点)进行路径压缩
// 并查集的查找函数
int find(int x)
{if (p[x] == x || p[p[x]] == p[x]) return p[x]; // 如果x是根节点或者x的父节点是根节点,则返回xint r = find(p[x]); // 递归查找x的根节点// 路径压缩,将x的父节点更新为根节点,同时更新距离d[x] += d[p[x]];p[x] = r;return r;
} 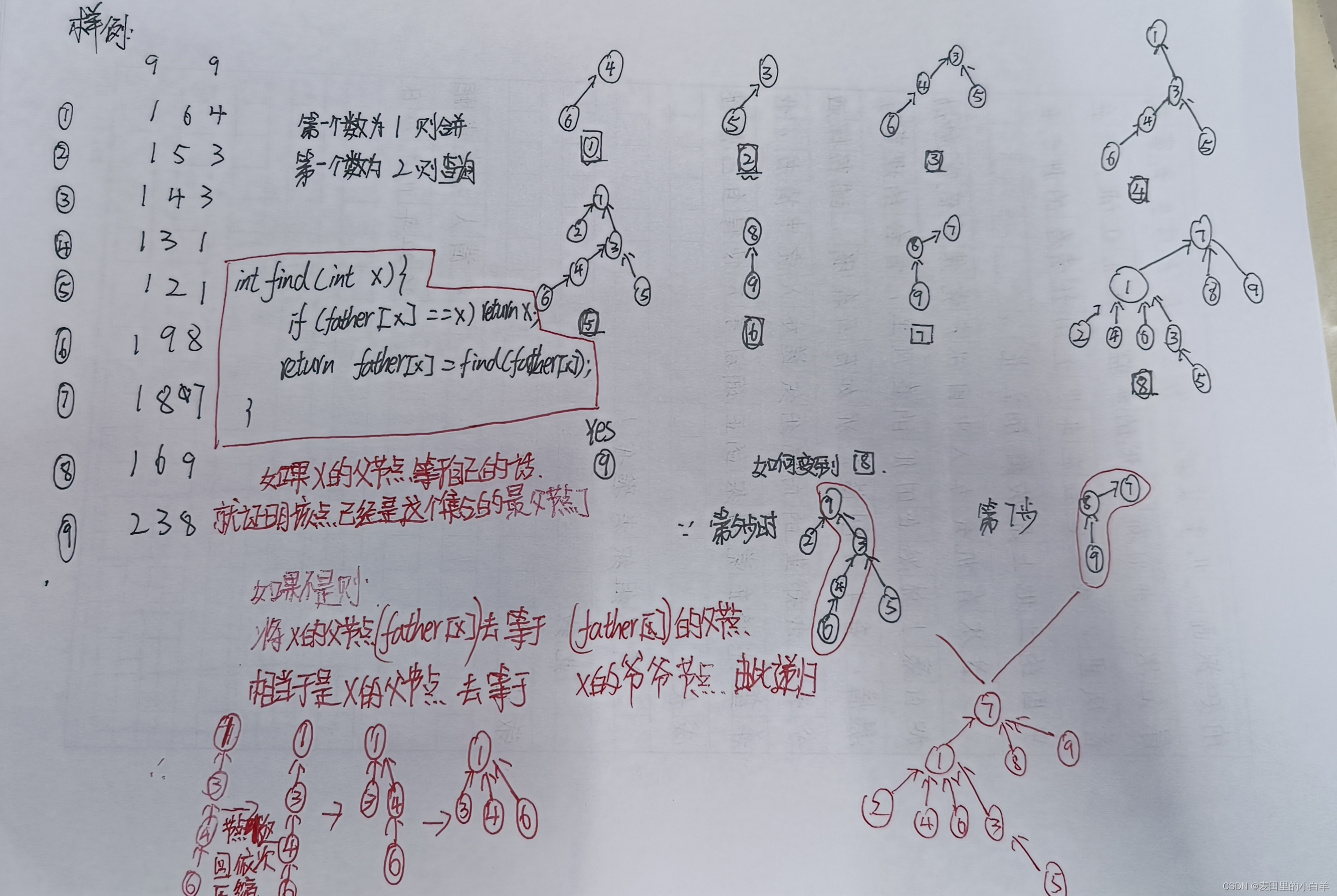
第五:这是我给大家画的样例图片,大家可以好好照着理解一下,理解一下什么是路径压缩,他是运用递归的思想,不断向上去寻找最根节点的根节点在哪里 , 找到了之后我们就依次返回,最终将路径上的每个点的父节点都变为根节点
代码:
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 10010;int n, m;
int p[N], d[N];// 并查集的查找函数
int find(int x)
{if (p[x] == x || p[p[x]] == p[x]) return p[x]; // 如果x是根节点或者x的父节点是根节点,则返回xint r = find(p[x]); // 递归查找x的根节点// 路径压缩,将x的父节点更新为根节点,同时更新距离d[x] += d[p[x]];p[x] = r;return r;
}int main()
{scanf("%d%d", &n, &m); // 读取节点数和操作数for (int i = 1; i <= n; i ++ ) p[i] = i; // 初始化并查集的父节点为自身while (m -- ){int t, a, b;scanf("%d%d%d", &t, &a, &b); // 读取操作类型和操作数if (t == 1){a = find(a), b = find(b); // 查找a和b所属的集合的根节点if (a != b) // 如果a和b不在同一个集合中{d[a] -= d[b]; // 更新a的距离p[a] = b; // 将a所属的集合合并到b所属的集合中}}else{a = find(a); // 查找a所属的集合的根节点d[a] += b; // 更新a所属集合中的所有节点的距离(距离增加b)}}for (int i = 1; i <= n; i ++ )if ( i == find(i) ) printf("%d ", d[i]); // 输出根节点的距离else printf("%d ", d[i] + d[find(i)]); // 输出非根节点的距离(距离需要累加)puts("");return 0;
}这篇关于网络分析(蓝桥杯,acwing,并查集)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





