【聚类】K-Means聚类（优缺点、手肘法、轮廓系数法、检测异常点、图像压缩，含代码实战）

本文主要是介绍【聚类】K-Means聚类（优缺点、手肘法、轮廓系数法、检测异常点、图像压缩，含代码实战），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

写在前面：
首先感谢兄弟们的关注和订阅，让我有创作的动力，请一键三连，在创作过程我会尽最大能力，保证作品的质量，如果有问题，可以私信我，让我们携手共进，共创辉煌。

1、介绍

K-Means 是一种简单但功能强大的无监督学习算法，是一种常用的基于距离的聚类算法。K-means算法基本思想是将样本数据划分为K个类别，使得每个数据点与其所属类别的聚类中心之间的距离最小化，从而达到聚类的目的。K-Means 聚类算法可以用于客户类型划分、异常点检测和图像压缩等。

2、原理

K-Means 具体流程如下：

1. 随机选择K个点作为初始聚类中心；
2. 计算每个数据点与K个聚类中心的距离，并将其归到距离最近的聚类中心的类别中；
3. 更新聚类中心的位置，将每个聚类中心的位置移动到其类别中所有点的均值位置；
4. 重复第2和第3步，直到聚类中心不再改变或达到最大迭代次数。

3、K值选择

通常使用手肘法或者轮廓系数法确定K值。

3.1手肘法

SSE，sum of the squared errors，误差的平方和。在K-means 算法中，SSE 计算的是每类中心点与其同类成员距离的平方和。

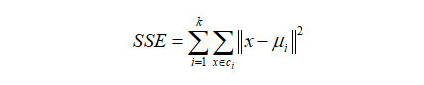
基本思想：

随着聚类数k的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和SSE自然会逐渐变小。

当k小于最佳聚类数时，k的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大；

当k到达最佳聚类数时，再增加k所得到的聚合程度，回报会迅速变小，所以SSE的下降幅度会骤减，然后随着k值的继续增大而趋于平缓。

也就是说SSE和 k 的关系图是一个手肘的形状，而这个肘部对应的k值就是数据的最佳聚类数。这也是该方法被称为手肘法的原因。

3.2轮廓系数法

轮廓系数（Silhouette Coefficient）结合了聚类的凝聚度（Cohesion）和分离度（Separation），用于评估聚类的效果。该值处于-1~1之间，值越大，表示聚类效果越好。

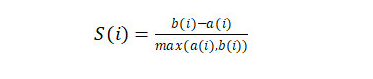
求出所有样本的轮廓系数后再求平均值就得到了平均轮廓系数。平均轮廓系数的取值范围为[-1,1]，且簇内样本的距离越近，簇间样本距离越远，平均轮廓系数越大，聚类效果越好。那么，很自然地，平均轮廓系数最大的k便是最佳聚类数。

4、优缺点

4.1优点

（1）简单直观，容易理解：K-Means算法原理比较简单，实现容易，聚类效果也不错；

（2）处理大数据集效率高：处理大数据集的时候，该算法可以保证较好的伸缩性；

（3）可解释性强：每个簇都有一个中心点，可以用来解释和描述该簇的特征。

4.2缺点

（1）对初始簇中心敏感：不同的初始簇中心可能导致不同的聚类结果；

（2）K值需要人为设定：需要预先指定聚类的簇数K，这个值的选择通常比较困难，需要基于经验或尝试不同的值来确定；

（3）对噪声和异常值敏感：噪声和异常值可能会对K-Means算法的聚类结果产生较大的影响，导致簇的中心偏移或产生不理想的簇；

（4）不适合非凸形状簇：K-Means算法假设簇的形状是凸的（或至少是圆形的），对于非凸形状或形状大小差异较大的簇，可能无法得到好的聚类效果。

5、复杂度

时间复杂度： O(tknm)，其中，t 为迭代次数，k 为簇的数目，n 为样本点数，m 为样本点维度。

空间复杂度： O(m(n+k))，其中，k 为簇的数目，m 为样本点维度，n 为样本点数。

6、代码实战

6.1数据划分

# -*- coding: utf-8 -*-
"""
Created on Tue Mar 19 18:45:10 2024@author: zqq
"""from sklearn.datasets import make_blobs  
import joblib
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score# 数据, 1000个样本点，3个簇
X, y = make_blobs(n_samples=1000, n_features=2, centers=[[2,2],[4,4],[6,6]], cluster_std=[0.2,0.4,0.5], random_state=2)# 查看原始数据
plt.figure()
plt.scatter(X[:,0], X[:,1], marker='o')
plt.show()# 手肘法, 确定K值
SSE = []
k_min = 1
k_max = 10
for k in range(k_min, k_max):print("k:", k)kmeans_model = KMeans(n_clusters=k, random_state=10)kmeans_model.fit(X)SSE.append(kmeans_model.inertia_)
# 绘图
plt.figure()
plt.plot(range(k_min, k_max), SSE, marker='x')    
plt.title('The Elbow method')
plt.xlabel('k')
plt.ylabel('SSE')
plt.show()# 轮廓系数法，确定K值
SC = []
k_min = 2  # 轮廓系数必须从2开始
k_max = 10
for k in range(k_min, k_max):print("k:", k)kmeans_model = KMeans(n_clusters=k, random_state=10)kmeans_model.fit(X)sc_score  = silhouette_score(X, kmeans_model.labels_)SC.append(sc_score)
# 绘图
plt.figure()
plt.plot(range(k_min, k_max), SC, marker='o')    
plt.title('The sihouette coefficient method')
plt.xlabel('k')
plt.ylabel('sihouette coefficient score')
plt.show() # 保存模型
kmeans_model = KMeans(n_clusters=3, random_state=10)
kmeans_model.fit(X)
joblib.dump(kmeans_model, 'kmeans_model.pkl')
y_pred = kmeans_model.predict(X)
plt.figure()
plt.scatter(X[:,0], X[:,1], c=y_pred, s=10)
plt.show()

手肘法：

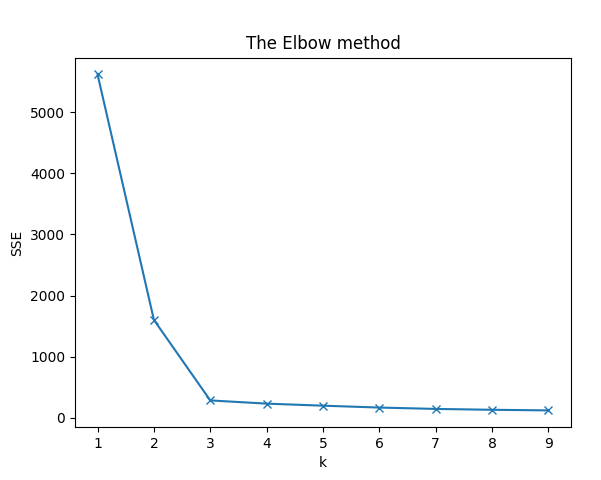
轮廓系数法：

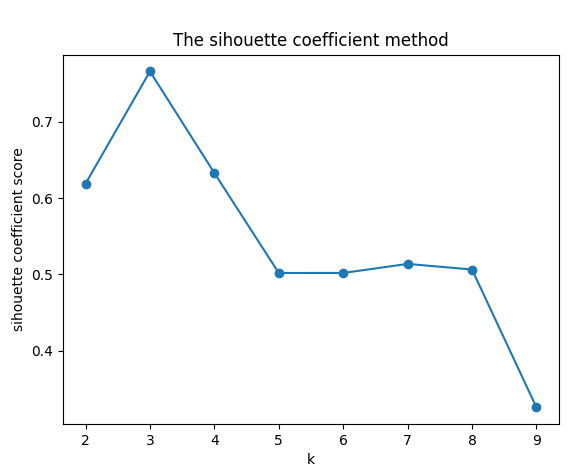
三类数据分布图：

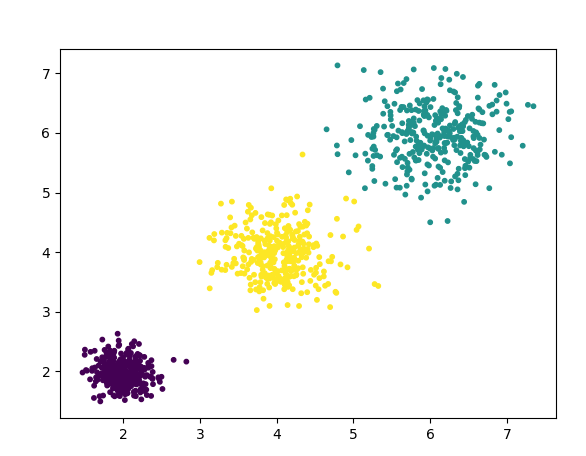
6.2检测异常点

# -*- coding: utf-8 -*-
"""
Created on Fri Mar 22 09:28:47 2024@author: zqq
"""from sklearn.cluster import KMeans
import numpy as np
from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt# 生成模拟数据
X = np.concatenate([np.random.normal(0, 1, (100, 2)), np.random.normal(10, 1, (10, 2))])# 可视化样本
plt.figure()
x = X[:,0]
y = X[:,1]
# s散点的面积，c散点颜色
plt.scatter(x, y, s=10, c='red')
plt.show()# KMeans算法拟合
kmeans_model = KMeans(n_clusters=2, random_state=0).fit(X)# 聚类中心
centroids = kmeans_model.cluster_centers_
print("聚类中心:\n", centroids) # 每个样本到上述聚类中心的距离，欧式距离
D = cdist(X, centroids, 'euclidean')# 每个样本的最近聚类中心索引
cluster_labels = D.argmin(axis=1)# 设置一个阈值，超过这个阈值认为是离群点
threshold = 2.5# 寻找离群点
outliers = [X[i] for i, d in enumerate(D) if d[cluster_labels[i]] > threshold]# 打印离群点
print("Outliers:\n", outliers)

原始数据分布图：

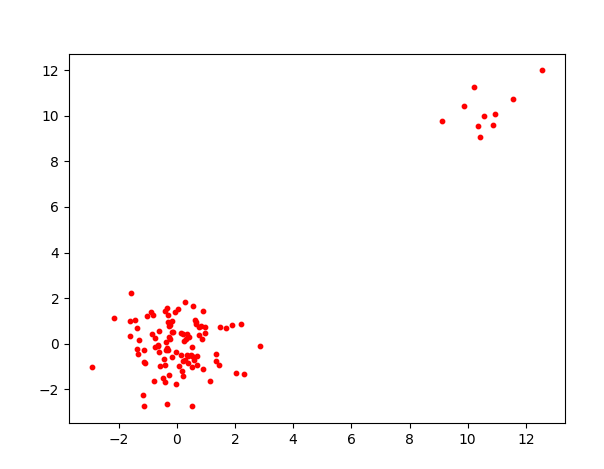
给出的异常点数据：

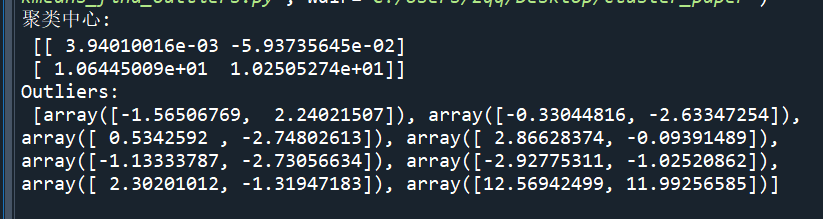
6.3图像压缩

# -*- coding: utf-8 -*-
"""
Created on Fri Mar 22 09:54:47 2024@author: zqq
"""import numpy as np  
from sklearn.cluster import KMeans  
from PIL import Image  
import matplotlib.pyplot as plt  # 加载图像并转换为numpy数组  
image = Image.open('flower.jpg').convert("RGB")image_array = np.array(image)  # 将图像数据重塑为二维数组，其中每一行是一个像素点的RGB值  
pixels = image_array.reshape(-1, 3)  # 使用K-Means算法对像素进行聚类  
n_colors = 8  # 设置颜色数量，这将影响压缩率  
kmeans = KMeans(n_clusters=n_colors)  
kmeans.fit(pixels)  # 使用K-Means聚类中心替换原始像素值  
compressed_pixels = kmeans.cluster_centers_[kmeans.labels_]  # 将压缩后的像素值重塑回原始图像的形状  
compressed_image_array = compressed_pixels.reshape(image_array.shape)  # 将压缩后的图像数组转换为图像对象  
compressed_image = Image.fromarray(np.uint8(compressed_image_array))  # 显示原始图像和压缩后的图像  
plt.figure(figsize=(10, 5))  plt.subplot(1, 2, 1)  
plt.imshow(image)  
plt.title('Original Image')  plt.subplot(1, 2, 2)  
plt.imshow(compressed_image)  
plt.title(f'Compressed Image with {n_colors} colors')  plt.show()  # 保存压缩后的图像  
compressed_image.save('compressed_image.jpg')

原始图像：

压缩图像：

参考资料

https://blog.csdn.net/m0_62110645/article/details/134148972
https://zhuanlan.zhihu.com/p/78798251
https://zhuanlan.zhihu.com/p/619922019
https://blog.csdn.net/wsgzjdbb/article/details/106931273
https://blog.51cto.com/u_15060465/4297864
https://www.cnblogs.com/SpaldingWen/p/9960991.html
https://mp.weixin.qq.com/s/FRe7A6Zo9iX7IqOpYofLYg
https://blog.csdn.net/zly_Always_be/article/details/136109128
https://blog.csdn.net/qq_34448345/article/details/127407274
https://blog.csdn.net/wfh684066/article/details/81006472
https://zhuanlan.zhihu.com/p/54045059

这篇关于【聚类】K-Means聚类（优缺点、手肘法、轮廓系数法、检测异常点、图像压缩，含代码实战）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---