深度学习 Lecture 4 Adam算法、全连接层与卷积层的区别、图计算和反向传播

本文主要是介绍深度学习 Lecture 4 Adam算法、全连接层与卷积层的区别、图计算和反向传播，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、Adam算法（自适应矩估计）

全名：Adapative Moment Estimation

目的：最小化代价函数（和梯度下降一样）

本质：根据更新学习率后的情况自动更新学习率的值(可能是自动增大，也可能是自动变小）

它在全局不止有一个学习率，就是说每个式子的学习率都有可能有所不同。

优点：对学习率的选择更具有鲁棒性，通常比梯度下降还要快

注意：在代码中设置它的时候需要标注一个初始的学习率先

代码：

这里把初始学习率设置为le-3了

from_logits = True是为了让计算结果更加精确

SparseCategoricalCrossentropy是稀疏矩阵的交叉熵，它可以让结果出现在某个范围中

二、全连接层 (Dense layer)

含义：就是这一层里的每个神经元都从前一层得到所有的激活

三、卷积层（Convolutional layer)

含义：每个神经元只得到一部分

比如说，对于一张图片，卷积层是只接收图片的某一部份数据的，而不是整张图片

作用：

1. 加快计算速度

2.需要的数据较少

3.不容易过拟合

如果在神经网络中有多个卷积层，这个神经网络就叫卷积神经网络。

四、图计算（Computation graph)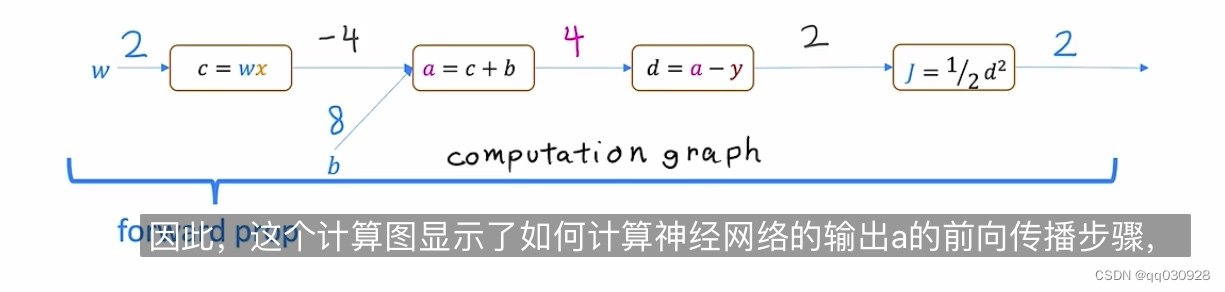

就是，一组节点，这些节点通过边缘或箭头相连，其实就是把每个计算步骤，单独作为一个步骤，去一步一步计算。

五、反向传播（back prop)

上图是前向传播，就是从左到右进行一步一步的计算，而反向传播就是从右到左，计算导数。

在机器学习中,很多算法最后都会转化为求一个目标损失函数（loss function）的最小值。这个损失函数往往很复杂，难以求出最值的解析表达式。而梯度下降法正是为了解决这类问题。直观地说一下这个方法的思想：我们把求解损失函数最小值的过程看做“站在山坡某处去寻找山坡的最低点”。我们并不知道最低点的确切位置，“梯度下降”的策略是每次向“下坡路”的方向走一小步，经过长时间的走“下坡路”最后的停留位置也大概率在最低点附近。这个“下坡路的方向”我们选做是梯度方向的负方向，选这个方向是因为每个点的梯度负方向是在该点处函数下坡最陡的方向。至于为什么梯度负方向是函数下降最陡的方向请参考大一下的微积分教材，或者看看这个直观的解释。在神经网络模型中反向传播算法的作用就是要求出这个梯度值，从而后续用梯度下降去更新模型参数。反向传播算法从模型的输出层开始，利用函数求导的链式法则，逐层从后向前求出模型梯度。

比如上图的最终计算节点是J = d^2/2，反向传播的第一步将询问如果d的值稍微改变一点，那j的值会改变多少？

假如算出来是2，就在J到d的这个板块的方向上写一个2，这个值是j对于输入值d的导数

这是第一步。

下一步是查看之前的节点，并询问j对于a的导数是什么？

算出来是2，就在d-a这个线上写2。

照这样的思路，一直往前推j对每个参数的导数，一直推到j对最前面（第一个输入值）的导数，在这里面是w。