二、永磁同步电机矢量控制(FOC)—不同坐标系下电机数学模型

1.电机数学模型

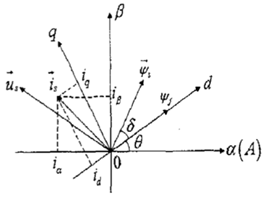
       对于永磁同步电机，矢量控制算法是建立在电机的数学模型上，在不同坐标系下，电机数学模型也不同，主要分为自然坐标系ABC下的PMSM数学模型、两相静止坐标系aβ下的PMSM数学模型和两相旋转坐标系dq下的PMSM数学模型。

       矢量控制中是进行磁场定向控制，包括转子磁场定向、定子磁场定向和气隙磁场定向。矢量控制基于转子磁场控制，直接转矩控制基于定子磁场定向。

       矢量控制中使用最多的是两相旋转坐标系dq下的PMSM数学模型。

        假设：（1）相绕组、定子电流、转子磁场都对称；（2）转子无阻尼绕组；（3）忽略磁场饱和(磁感应强度和磁场强度呈现线性关系)，不计涡流和磁滞损耗(电能均转化为电枢、气隙存储的磁场能量和转子的机械能)，气隙磁密波形为正弦波。

2.三相静止坐标系ABC下的PMSM数学模型

（1）电压方程

补充，以上电压、电流、磁链均为瞬时值

（2）磁链方程

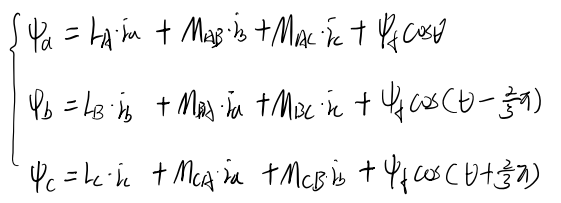
L_A为三相定子绕组自感，M_AB为定子绕组自感，若各相绕组匝数相同，自感值等于互感值，φf为转子永磁体励磁磁链，θ为θe电角度

CSDN博主昔时扬尘处给的公式

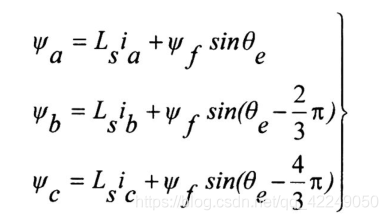
（3）电磁转矩方程

       根据机电能量转化原理，电磁转矩Te等于磁场能量对机械角度θm的偏导。

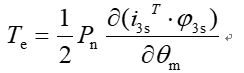
       若通过三线电流计算输出转矩

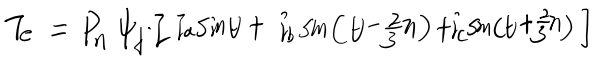
Pn为磁极对数，

（4）机械运动方程

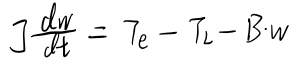
Te为电磁转矩，TL为负载转矩，J为转动惯量，B为阻尼系数，此处w为机械角速度wm，单位为rad/s。

3.两相静止坐标系αβ下的PMSM数学模型

（1）电压方程

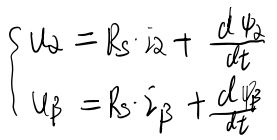
为α轴磁链

（2）磁链方程

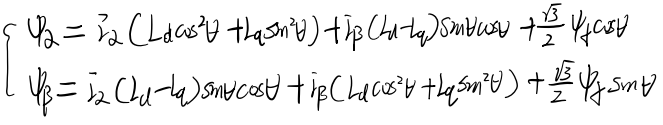
Ld、Lq分别为交直轴电感，对于表贴式PMSM，Ls(定子电感)=Ld=Lq

CSDN博主昔时扬尘处给的公式

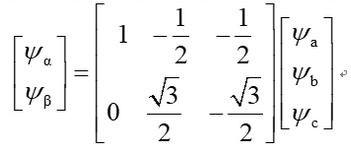
（3）电磁转矩方程

CSDN博主昔时扬尘处给的公式

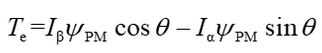
4.两相旋转坐标系dq下的PMSM数学模型

（1）电压方程

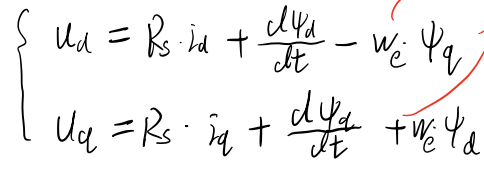
电角速度

将交直轴电压进行等效

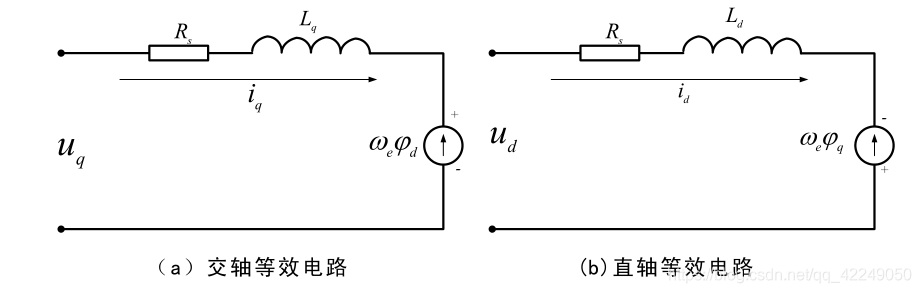
（2）磁链方程

同步旋转坐标系下的表贴式永磁同步电机有Ld(直轴电感)=Lq(交轴电感)=Ls

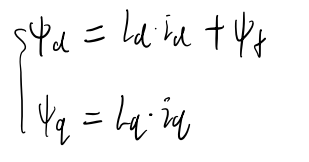
为转子永磁体励磁磁链。

（3）电磁转矩方程

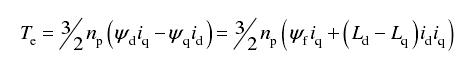
电磁转矩由两部分组成，第一项是永磁体和定子绕组磁链之间相互作用产生，第二项是由于磁阻变化产生，隐极电机Lq=Ld不存在磁阻变化，磁阻变化转矩是凸极电机特有的。

由于表贴式(隐极)永磁同步电机交直轴电感相同，转矩方程转变为下式：

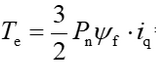
对转矩电流iq进行控制，就可以有效控制电磁转矩。磁极对数和转子磁链为已知量。

5.补充

内置式永磁同步电机的凸极效应使得磁路交叉饱和严重。在电机高速运行期间，电机参数发生非线性变化，主要是由于磁饱和（可分为饱和和交叉饱和）以及电机长时间运行温度升高、趋肤效应导致的参数变化。

（1）磁阻和电感的关系：

        磁阻越大，电感越小

        磁阻

        磁动势f=N(封闭线圈匝数)*i(通过该线圈的电流)=磁阻*磁通量，若电流发生变化，则磁动势变化，磁阻越大，磁通量变化越小。

        磁阻变化导致线圈磁通量变化，电感的大小由于磁通量的变化率有关，当磁场分布发生变化时，电感也会随之变化。

（2）凸极效应：凸极电机的气隙不均匀，也即直轴（d轴）和交轴（q轴）的有效气隙不同，导致气隙磁场不均匀。交-直轴电枢反应电抗对电机性能的影响称为凸极效应。电枢反应磁场的作用使磁阻发生很大变化，d 轴电感和 q 轴电感不相等（凸极电机Ld<Lq），交直轴磁路不同，因此交直轴磁阻不同，最终导致交直轴电感不一样

（3）d轴磁路由气隙、永磁体、铁芯组成（永磁体与气隙磁导率较低，磁阻较大），q轴磁路由气隙和铁芯组成（铁芯会出现磁路饱和问题），d轴磁阻较大，则d轴电感较小。由于q轴电流增大，所以q轴磁路中出现饱和，q轴电感相应减小

（4）磁饱和现象：磁饱和是磁性材料的物理特性，其通过的磁通不能无限增大，达到一定值时，即使增大电流和线圈匝数都无法提高磁通密度。当磁场强度逐渐增加，磁导率逐渐减小，磁感应强度与磁场强度不再为线性关系。硅钢片把电能转化成磁能再转化成动能的能力是有限的。当电机电流超过一定范围后,电能无法再转化成更多的磁能,只能转化成热能,导致电机迅速升温,这是磁饱和的后果。

（5）趋肤效应：当导体中有交流电或者交变电磁场时，导体内部的电流分布不均匀，电流集中在导体的“皮肤”部分，也就是说电流集中在导体外表的薄层，越靠近导体表面，电流密度越大，导体内部实际上电流较小，结果使导体的电阻增加，使它的损耗功率也增加。电阻随温度升高而升；磁链随温度升高会降低。