论文笔记 - Omnidirectional stereo depth estimation based on spherical deep network

论文笔记 Omnidirectional stereo depth estimation based on spherical deep network

本文是2021 Image and Vision Computing上的一篇文章。IVC算是领域内认可度较高的期刊之一。本文针对双目全景深度估计，提出了基于球面卷积的级联网络，将全景图的平面投影转换到球面表示，获取了高精度的全景深度图。
本文链接 https://www.sciencedirect.com/science/article/abs/pii/S0262885621001694
代码位于CSDNet

本文指出，全景相机在现阶段的广泛使用使全景深度估计称为当前热点问题之一。但是，现有的全身深度估计方法基本都是由平面立体深度估计算法发展而来，从而引入了非线性的对极约束以及投影过程中的畸变。本文提出了一种基于球面卷积和球面对极约束实现全景图深度估计。本文讨论了球面立体对极约束并且将全景图平面投影下的非线性约束转化为球面上的线性约束。文章提出了球面卷积残差网络（Spherical Convolution Residual Network, SCRN），输入的ERP投影图首先被采样为球面表示，然后送入SCRN获取球面信号下的深度图。文章接着提出了平面优化网络（Planar Refinement Network, PRN）并采用了级联式学习的策略对深度图进行细化调优。整体架构称为Cascade Spherical Depth Network (CSDNet)，级联球面深度网络CSDNet。该网络取得了SOTA的效果。

1. Introduction

文章在introduction部分提出，深度估计是计算机视觉的基础任务之一，具有广泛的应用，随着全景相机的普及，全景深度估计也受到关注。作者认为，在3D环境感知方面，普通平面相机需要多次拍摄才能获取全景的三维信息，而激光雷达虽然也具有全向深度感知能力，但是加个更贵，点云更稀疏。全景图像的深度估计是方便获取稠密三维信息的低成本方案。文章列举了一些在平面图像双目立体匹配与深度估计做的较好的算法，并提出全景相机获取的球面图像其对极约束与平面不同，且球面图像表示为平面投影时有很大的畸变。现有的全景深度估计方法大多来自于平面的算法，或者利用了球面图的不同投影方式，没有使用双目球面图像的对极约束信息。本文则分析了球面立体匹配约束关系，基于球面卷积 Mesh CNN提出了球面残差网络，计算球面信号表示下的深度值；然后重新投影到ERP表示并利用优化网络获取更加准确的深度图。

上图是论文中图1，展示了左右图的ERP投影图以及球面Mesh信号图，与论文模型得到了深度图、点云。

2. Related Work

本章作者对现有的平面深度估计与立体匹配、球面深度估计算法、球面卷积算法三个方面的相关工作进行了总结。

平面深度估计方面，文中分为了传统方法与深度学习方法。深度学习方法又分为了回归和Cost Volume两类。回归类就类似于DispNet这样将深度或视差估计视作从输入左右图到深度图/视差图的变换，通过端到端网络回归得到每个点的深度或视差值。Cost Volume则更偏向于传统算法发展而来的立体匹配框架，即通过构建每个点在不同视差值的匹配代价，找到最佳匹配的视差值，不过特征提取、匹配代价计算等步骤均有深度网络完成，而不是以前的汉明距离、SGM等等这一系列了。文章也提到，由于现有的全景图大多以ERP投影形式存在，这种投影下的对极约束与平面不同，因此对Cost Volume类实现起来有所困难。本文将球面深度估计视作球面上的回归问题，与之对比的方法也基本如此。

球面深度估计领域，作者未做详细的分类，看下来大致是这样的。双目的球面深度估计只提到了一篇360SD-Net，是通过上下两个相机的视角实现立体匹配的。单目的是主流，主要有两类，一类是参考平面单目深度估计发展而来的方法，另一类以BiFuse、UniFuse为代表的融合不同投影方式的全景图，以追求避免单一投影下的畸变问题。当然还有一类是通过4个鱼眼相机获取全景信息，但不拼接为全景图像，而是直接以多视角鱼眼相机为输入估计全景深度的方法。
以单目为主可能与数据集的关系较大。文章指出，全景深度估计领域的公开数据集，大多以单目的ERP投影为可见光输入，主要场景为室内，典型的有Matterport3D、SunCG、PanoSuncg、Stanford2D3D等。另一研究团队提出3D60数据集，通过视角变换得到三个视角的图像：上、下/左、右，3D60的源数据来自于上述几个单目数据集，并在其基础上发展出了多目全景深度数据集。本文的实验是基于Matterport3D和3D60进行的。

文章还对近年来球面卷积相关的工作进行了简要总结。球面卷积是近年来机器学习领域的新兴热点之一，主要为了解决球面信号（如全景图）的卷积运算问题。其主要思路有两类，一类是对卷积进行适应性变形，避免畸变带来的影响，这一类方法出发点较为朴素，仍然遵循一般二维卷积的思路，只是采样时不完全是邻域，而是球面上真实的相邻点；但是问题也在于需要针对球面信号的投影方式改变采样方式。另一类则是将球面投影图转化为其他域的信号表示，利用信号处理方式（傅里叶变换）等表征卷积操作。文章使用的MeshCNN，就是将球面全景图通过Mesh，表示为球面上三角形的点面mesh形式，相当于对一个曲面（即球面）表示为三角形mesh，通过顶点的值和点之间的相邻关系表示一个球面。球面图像先被采样并表示为Mesh形式，根据记录的相邻关系计算卷积。此时相邻点不再受畸变影响。

3. Spherical imaging and projection of omnidirectional stereo

本文首先对球面立体成像模型与投影方式做了介绍。全景相机的成像面是一个球面，简单理解，空间中的点发出或反射的光线与球心（光心）连线与球面的交点，就是该点在全景相机成像的像点。不同于平面立体几何中的对极约束为一条直线。本文指出，球面上的对极约束是球上的一个大圆，也就是说，空间当中的一个点，成像在左右全景相机球面上，均会落在同一个球面方程所约束的大圆上。

本文对于球面对极约束及其ERP投影变换的图解见上图。

本文也推导了笛卡尔坐标系与球坐标系的转换，以及球面图投影到ERP图像的变换关系，得到了空间中的点在球面成像并投影为ERP的变换关系，也即从空间中(x, y, z)到ERP图像上(u, v)的变换。文章也指出，球面上的大圆（也就是空间中的水平线）在ERP投影上变成了正弦型曲线，这也导致了ERP投影下的球面立体几何不再满足线性的对极约束。

如图所示，左图中的点，在右图中的对应点位于相应的大圆上，表现在ERP投影上，就是在相应的正弦曲线上。位于不同俯仰角的大圆，其投影后的曲线也不同（赤道可以保持为直线）。

因此本文采用球面卷积，在球面信号表示下进行深度估计。

4. A novel spherical deep network for omnidirectional depth estimation

本文首先利用MeshCNN搭建球面特征提取模块，构造了由mesh球面卷积与1x1卷积构成的球面下采样、卷积块与上采样模块。MeshCNN将球面图像表示为球面Mesh信号，每个点的值以一维张量存储，同时记录点之间的相邻关系。meshCNN本身可以实现空域（邻接点）的卷积，而通过1x1卷积进一步增强通道维度的联系。

本文提出了球面卷积残差网络Spherical Convolution Residual Network, SCRN）。由基于球面卷积的上下采样对以及球面残差模块串联而成，基本结构为先下采样，然后经过若干残差模块，再进行上采样。通过这个SCRN实现了球面信号表示下的深度估计。

然而，文章指出，得到的球面深度信号受到球面采样密度的限制，同时从ERP到球面的正反投影过程都会带来额外的误差与噪声。因此文章提出了级联式的学习模式，以及平面细化网络（Planar Refinement Network, PRN）。将SCRN输出的球面深度信号，再次投影到ERP域，然后结合左右图，输入到PRN中，得到更加完善的深度图。

如上图所示，本文的整体网络结构是级联的二阶段结构，第一阶段通过SCRN计算球面信号表示下的深度信号，然后再次投影为ERP图像，第二阶段通过PRN对深度图进行进一步的调优。

训练阶段，文章将输出的球面深度信号、投影得到的ERP深度图，以及最后输出的优化后深度图都作为监督的目标，使用BerHu损失函数进行监督学习，同时加入了平滑项。


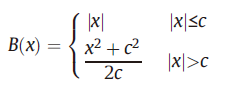
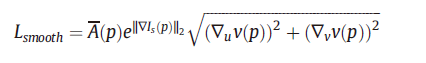
最终的损失函数是球面深度信号、ERP深度图的损失与平滑项的加权和：

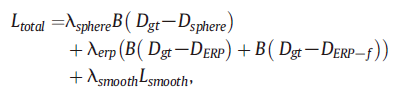
5&6. Experiments, Ablation study

大部分全景深度数据集均为单目，而3D60数据集则是将多个单目数据集通过视角生成获得多目图像数据。本文选取了3D60的官方数据划分之一用于3D60数据集上的评估；此外还使用其中视角生成的Matterport3D数据进行了训练与测试。两个数据集上的结果与全景深度估计的SOTA算法（CoordNet，BiFuse，UniFuse）以及平面双目的一些算法（DispNet，CRL）进行了对比。性能达到了SOTA水平，同时由于MeshCNN的使用，其参数量要小于其他几种算法模型。

在消融实验部分，本文研究了级联两个阶段，以及将整体CSDNet中的球面卷积换成平面卷积所取得的结果。对比验证了球面卷积与级联学习策略的作用。同时由于球面卷积性能受到Mesh采样密度的影响，作者在不同等级的Mesh密度下进行了对比。

这里展示一下3D60数据集的对比结果，其他结果图表详见论文。总体而言，文章提出的CSDNet在公开全景深度数据集上取得了比较好的效果，同时MeshCNN的加入使得网络整体参数量更小。实验表明，球面卷积对于球面信号的处理能够利用球面的对极约束信息，克服畸变，其效果由于同等结构与参数量的平面网络。另外级联学习的作用也在实验中有所体现，分阶段的深度估计也是近年来很多工作研究方向之一。Mesh级别，也即采样密度，在文中也进行了讨论，随着采样点数量与密度提升，精度也随之增加，但是时间与计算资源开销也会增大，在实际使用中可以根据速度与精度的实际需求进行取舍。

7. Discussion and Conclusion

总结部分，文章提到了SCRN在一些不需要输出深度图，只需要获得深度点云的场景中可以直接使用，而不需要投影。指出了MeshCNN实现中一些消耗显存的地方，讨论了基于立体匹配中Cost Volume方法进行球面立体匹配的可能。

总体而言，本文着重于全景深度估计这一近年来逐渐受到关注的问题，创新地采用了球面表示方法与球面卷积来解决全景图像非线性的对极约束，以及在平面投影中无法忽略的巨大畸变。结果在公开数据集上表现不错。对于这一领域的思路有一定的启发作用。