本文主要是介绍线性代数(主题篇):Ch3.向量组 、Ch4.方程组,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 第3章 n维向量
- 1.概念
- (1)n维向量
- (2)n维非零列向量的性质
- 2.向量、向量组的的线性关系(线性相关性)
- (1)线性表示 :AX=β
- (2)线性相关、线性无关: AX=0
- ①线性相关
- ②线性无关
- ③线性相关性7大定理
- 向量:个数与维数
- ④例题:线性相关、线性无关
- 3.极大线性无关组、等价向量组、向量组的秩
- 1.极大线性无关组
- 2.向量组等价
- 3.向量组的秩
- 4.向量空间
- (1)向量空间的概念
- (2)基
- (3)基变换的过渡矩阵
- (4)向量在基下的坐标
- 5.空间直线
- 第4章 线性方程组
- (一)具体型线性方程组
- 1.齐次线性方程组 Ax=0
- (1)有解的条件:齐次线性方程组解的判别
- (2)解的性质:齐次解的性质
- 解的叠加性:解的线性组合也是解
- (3)基础解系、通解的结构
- ①基础解系
- ②通解的结构
- ③自由变量
- (4)求齐次方程组Ax=0的通解 (解齐次线性方程组)
- 2.非齐次线性方程组 Ax=β
- (1)非齐次线性方程组有解的条件
- (2)解的性质:非齐次解的性质
- (3)求非齐次方程组Ax=b的通解
- (4)非齐次线性方程组的几何意义
- 3.矩阵方程 AX=B
- (二)抽象型线性方程组
- (三)方程组的公共解、同解方程组
- 1.方程组的公共解
- 2.同解方程组
第3章 n维向量
1.概念
§ 3 §3 §3 向量组 { ①部分相关,整体相关 ②整体无关,部分无关 ③低维无关,高维无关 ④高维相关,低维相关 \begin{cases} ①部分相关,整体相关\\ ②整体无关,部分无关\\ ③低维无关,高维无关\\ ④高维相关,低维相关 \end{cases} ⎩ ⎨ ⎧①部分相关,整体相关②整体无关,部分无关③低维无关,高维无关④高维相关,低维相关
(1)n维向量
α = ( a 1 a 2 a 3 . . . a n ) , α T = ( a 1 , a 2 , a 3 , . . . , a n ) α=\left(\begin{array}{c} a_1 \\ a_2 \\ a_3 \\ ...\\ a_n \end{array}\right),α^T=(a_1,a_2,a_3,...,a_n) α= a1a2a3...an ,αT=(a1,a2,a3,...,an)
(2)n维非零列向量的性质
1.若 α α α为非零列向量,则:
(1) α α T αα^T ααT是秩一矩阵 【证明: r ( α α T ) ≤ r ( α ) = 1 r(αα^T)≤r(α)=1 r(ααT)≤r(α)=1】
(2) t r ( α α T ) = α T α \rm tr(αα^T)=α^Tα tr(ααT)=αTα 【若 α α α为单位列向量,则 t r ( α α T ) = α T α = 1 \rm tr(αα^T)=α^Tα=1 tr(ααT)=αTα=1】
(3) α α T αα^T ααT的特征值为 t r ( α α T ) = α T α , 0 , 0 \rm tr(αα^T)=α^Tα,0,0 tr(ααT)=αTα,0,0,即 α ⋅ α T ∼ ( t r ( α α T ) 0 . . . 0 ) α·α^T\sim\left(\begin{array}{cc} \rm tr(αα^T) & & \\ & 0 & \\ & & ...\\ & & & 0 \end{array}\right) α⋅αT∼ tr(ααT)0...0
2.对任意非零列向量 α,β,有以下性质:
① r ( β α T ) = r ( α α T ) = r ( β β T ) = 1 \rm r(βα^T)=r(αα^T)=r(ββ^T)=1 r(βαT)=r(ααT)=r(ββT)=1 【2013年21(2)】
② t r ( β α T ) = α T β \rm tr(βα^T)=α^Tβ tr(βαT)=αTβ, t r ( α α T ) = α T α , t r ( β β T ) = β T β \rm tr(αα^T)=α^Tα,tr(ββ^T)=β^Tβ tr(ααT)=αTα,tr(ββT)=βTβ
例题1:17年5.

分析:A不可逆 ⇦⇨ A有零特征值
∵α为单位列向量 ∴ t r ( α α T ) = α T α = 1 tr(αα^T)=α^Tα=1 tr(ααT)=αTα=1
又∵ r ( α α T ) ≤ r ( α ) = 1 r(αα^T)≤r(α)=1 r(ααT)≤r(α)=1 ∴ α α T αα^T ααT的特征值为 t r ( α α T ) tr(αα^T) tr(ααT),0,0,…,即1,0,0,…
而单位矩阵E的特征值为:1,1,1,…
由特征值的性质:设 f ( x ) f(x) f(x)为多项式,若 λ 1 , λ 2 , . . . , λ n λ_1,λ_2,...,λ_n λ1,λ2,...,λn为A的特征值,则 f ( λ 1 ) , f ( λ 2 ) , . . . , f ( λ n ) f(λ_1),f(λ_2),...,f(λ_n) f(λ1),f(λ2),...,f(λn)为 f ( A ) f(A) f(A)的特征值
则
A: E − α α T E-αα^T E−ααT的特征值为 (1,1,1)-(1,0,0)=0,1,1
B: E + α α T E+αα^T E+ααT的特征值为 (1,1,1)+(1,0,0)=2,1,1
C: E + 2 α α T E+2αα^T E+2ααT的特征值为 (1,1,1)+(2,0,0)=3,1,1
D: E − 2 α α T E-2αα^T E−2ααT的特征值为 (1,1,1)-(2,0,0)= -1,1,1
可见,A: E − α α T E-αα^T E−ααT有零特征值,不可逆

答案:A
例题2:09年13.
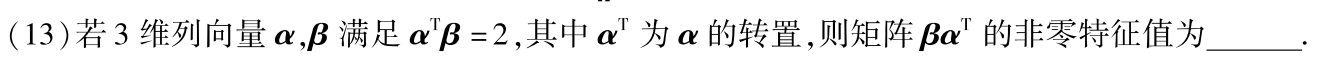
分析:
∵ r ( β α T ) = 1 r(βα^T)=1 r(βαT)=1
∴ β α T βα^T βαT的特征值为 t r ( β α T ) , 0 , 0 tr(βα^T),0,0 tr(βαT),0,0
而 t r ( β α T ) = α T β = 2 tr(βα^T)=α^Tβ=2 tr(βαT)=αTβ=2
答案:2
例题3:2013年21(2)

例题4:08年20.
例题5:24李林六(六)21.

2.向量、向量组的的线性关系(线性相关性)
(1)线性表示 :AX=β
若存在常数 k 1 , k 2 , . . . , k s , k_1,k_2,...,k_s, k1,k2,...,ks,使得 α = k 1 β 1 + k 2 β 2 + . . . + k s β s , α = k_1β_1+ k_2β_2+...+ k_sβ_s, α=k1β1+k2β2+...+ksβs,则称向量 α α α是向量组 β 1 , β 2 , . . . , β s β_1,β_2,...,β_s β1,β2,...,βs的线性组合,或称向量 α α α可被向量组 β 1 , β 2 , . . . , β s β_1,β_2,...,β_s β1,β2,...,βs线性表示(线性表出)
哪个向量前面的系数不为0,这个向量就可以被其余向量线性表示
例题1:03年10.
答案:D
例题2:数二 21年9. 线性表示

分析:

答案:D
(2)线性相关、线性无关: AX=0
①线性相关
1.定义:设向量组α1,α2,…,αs,若存在不全为0的数k1,k2,…,ks,使 k 1 α 1 + k 2 α 2 + . . . + k s α s = 0 k_1α_1+k_2α_2+...+k_sα_s=0 k1α1+k2α2+...+ksαs=0,则称向量组α1,α2,…,αs线性相关
2.线性相关的充要条件:α1,α2,…,αs中至少有一个向量可以被其他向量线性表示
线性相关的向量组中,系数不为0的向量,可由其他向量线性表示
3.线性相关的等价条件:
⇦⇨ 至少有一个向量可由其余n-1个向量线性表出

4.通过初等变换,无关 可变 相关,但 已相关 不可回 无关

5.含有零向量或成比例向量的向量组,必线性相关
显然,若向量组中有零向量,则向量组线性相关。(可取零向量α0的系数k0为任意非零常数,破坏了线性无关的定义。)
即含有零向量的向量组线性相关。
本来线性无关的向量组,加入一个零向量,它们就线性相关了。可见零向量就是一个润滑剂
②线性无关
1.定义:设向量组α1,α2,…,αs,若仅存在全为0的数 k1,k2,…,ks,使k1α1+k2α2+…+ksαs=0,则称向量组α1,α2,…,αs线性无关
2.推论:设向量组α1,α2,…,αs线性无关,但向量组α1,α2,…,αs,β线性相关。则向量β可由向量组α1,α2,…,αs线性表示,且表示法唯一。
3.线性无关的等价条件:
①线性无关的定义
②行列式 ∣ A ∣ ≠ 0 |A|≠0 ∣A∣=0
③A可逆
④满秩:r(A)=n
⑤AX=0仅有零解
⑥向量组不成比例
③线性相关性7大定理
1.线性相关 ⇦⇨ 至少有一个向量可由其余n-1向量线性表出
线性无关 ⇦⇨ 任一向量均不能由其余n-1个向量线性表出


2.原来无关,加一个相关,则新加的可被原向量组 唯一线性表示
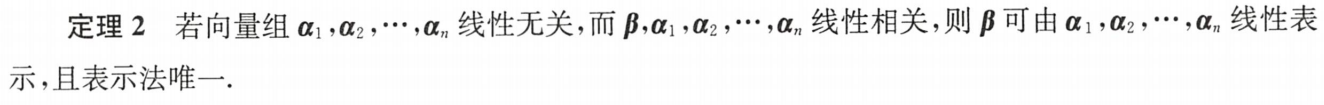
证明:


非0不可由0表示:若向量α第k行非0,其他向量第k行均为0,则α不可由其他向量线性表示
0向量可由非0向量表示:零向量 = 0×非零向量
3.以少表多,多的相关、秩多的可以表示秩少的
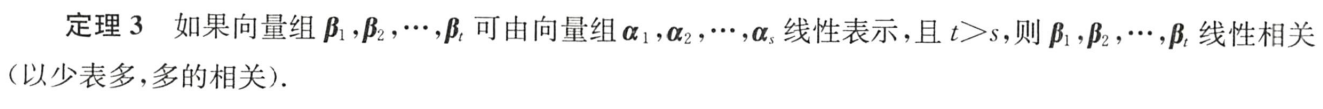
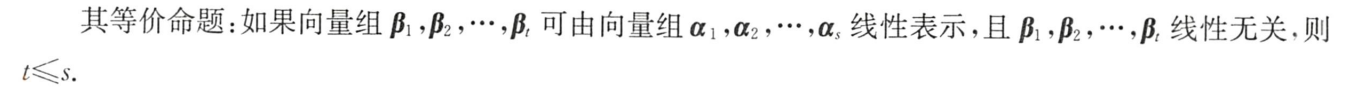
高维空间可表示低维空间,反之不可 【秩多的可以表示秩少的】
4.Ax=0 仅有零解,A线性无关;有非零解,A线性相关


向量:个数与维数
5个4维向量:一定线性相关
2个4维向量:可能相关,可能不相关。
①若向量组线性无关:则个数≤维数
②若个数>维数:一定线性相关
①n<m:必相关
Ⅰ.方程个数<未知数个数,即个数>维数,则线性相关。
Ⅱ.n维向量空间,若向量组线性无关,最多只能有n个向量。即个数≤维数。 (逆否命题)
个数≤维数,相关或无关 不一定。

②n=m:看行列式

③n>m:见定理6、7 + 方程组结论
5.①β可由向量组α₁,α₂,…,αm线性表出 ⇦⇨ An×mx = β 有解 ⇦⇨ r(A)=r(A,β)
②β不可由向量组α₁,α₂,…,αm线性表出 ⇦⇨ An×mx = β 无解 ⇦⇨ r(A)≠r(A,β)

6.向量个数的增减:
①部分相关,整体相关。
②整体无关,部分无关。
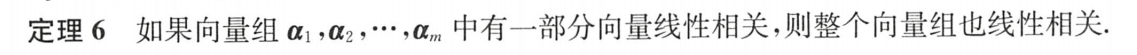

7.维数的增减:
①原来无关,延长必无关 【低维无关,高维无关】
②原来相关,缩短必相关 【高维相关,低维相关】

④例题:线性相关、线性无关
例题7:24李林六(四)6. 线性无关的定义

分析:
方法一:直接法

方法二:特殊值
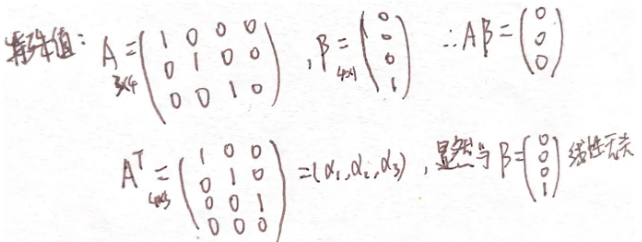
答案:D
例题2:20年21.

例题3:24李林六(一)21.

例题4:12年05.
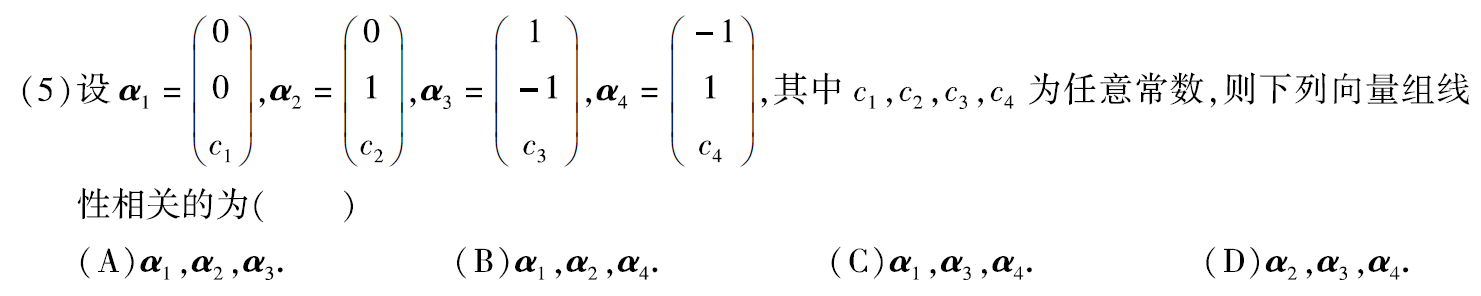
分析:
法一:线性相关的充要条件:线性相关⇦⇨行列式=0
∵|α1,α3,α4|=0,∴α1、α3、α4线性相关
法二:线性相关的充分条件:线性相关⇨成比例
∵α3+α4=(0,0,c3+c4)T,与α1成比例,∴α1、α3、α4线性相关
答案:C
例题5:06年11.

分析:
若已经相关了,则初等变换后依然相关,不能再变回无关了。(若变换后是无关,则变换前肯定也得是无关)
若本来无关,通过变换可能相关。
答案:A
例题6:06年11.真题的变式

答案:C
例题7:14年6. 线性无关、必要性与充分性

分析:
①必要性成立,是必要条件

②充分性不成立,是非充分条件(若向量组中有一个零向量,则该向量组线性相关)

答案:A
例题8:张宇30讲 例题3.6 抽象型向量组的线性相关性,用定义法

答案:


3.极大线性无关组、等价向量组、向量组的秩
1.极大线性无关组
(1)概念
①线性无关
②向量组中任意向量均可由极大线性无关组线性表出
(2)性质
①极大线性无关组一般不唯一,但其成员个数是唯一的。极大线性无关组是该向量组的最简小组
②向量组的秩:①极大线性无关组中成员的个数 ②向量组中线性无关的向量个数 ③秩为该向量组所张成的向量空间的维数

(3)找极大线性无关组的步骤
①将列向量们组成矩阵A,作初等行变换化为行阶梯形矩阵,确定r(A)
②按列找出其中一个秩为r(A)的子矩阵,即为一个极大线性无关组
2.向量组等价
1.矩阵等价:①同型 ②秩等:r(A)=r(B)
向量组等价:①同维 ②三秩相等:r(A)=r(B)=r(A,B) ,即两个向量组可以相互线性表出
2.初等行变换 ⇔ \Leftrightarrow ⇔ 行向量组等价 ⇔ \Leftrightarrow ⇔ 同解方程组 ⇔ \Leftrightarrow ⇔ r ( A ) = r ( B ) = r ( A B ) r(A)=r(B)=r\dbinom{A}{B} r(A)=r(B)=r(BA)
A经初等列变换得到B ⇔ \Leftrightarrow ⇔ 列向量组等价 ⇔ \Leftrightarrow ⇔ 矩阵方程 A X = B AX=B AX=B有解 ⇔ \Leftrightarrow ⇔ r ( A ) = r ( A , B ) r(A)=r(A,B) r(A)=r(A,B)
例题1:24李林六(五)6. 向量组等价:相互线性表出
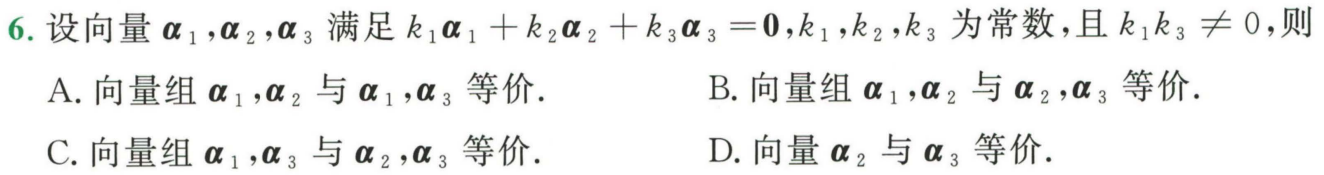
分析:

答案:B
例题2:13年5. 初等行变换:行向量组等价;初等列变换:列向量组等价

分析:
B可逆,AB=C即 A做初等列变换得到C。故A与C的列向量组等价
答案:B
例题3:23李林四(一)5. 初等行变换:行向量组等价;初等列变换:列向量组等价

分析:
初等行变换 ⇔ \Leftrightarrow ⇔ 行向量组等价 ⇔ \Leftrightarrow ⇔ 同解方程组
A经初等列变换得到B ⇔ \Leftrightarrow ⇔ 列向量组等价 ⇔ \Leftrightarrow ⇔ 矩阵方程 A X = B AX=B AX=B有解 ⇔ \Leftrightarrow ⇔ r ( A ) = r ( A , B ) r(A)=r(A,B) r(A)=r(A,B)
A.B.初等列变换 ⇔ \Leftrightarrow ⇔ 列向量组等价。A❌B✔
C.同解方程组是行向量组等价。C❌
D.初等变化不改变矩阵的秩,但可能改变矩阵的特征值和行列式。D❌
答案:B
例题4:00年9.

分析:
D.矩阵A满秩,则矩阵B满秩的充要条件是,矩阵A与矩阵B等价,则型同秩等。B也满秩。D✔
C.向量组等价,还多余一个可以相互线性表出的条件,是充分非必要条件。
举例:

答案:D
3.向量组的秩
1.向量组的秩的概念:
①向量组 α 1 , α 2 , . . . , α s α_1,α_2,...,α_s α1,α2,...,αs 的极大线性无关组 α i 1 , α i 2 , . . . , α i r α_{i_1},α_{i_2},...,α_{i_r} αi1,αi2,...,αir 中所含向量的个数r 为 向量组的秩,记作 r ( α 1 , α 2 , . . . , α s ) = r r(α_1,α_2,...,α_s)=r r(α1,α2,...,αs)=r
②向量组中线性无关的向量个数
③秩为该向量组所张成的向量空间的维数
2.性质:
①矩阵的秩 = 行秩 = 列秩 (三秩相等)
②秩大的表示秩小的,可被线性表出的秩小

4.向量空间
(1)向量空间的概念
过渡矩阵、坐标、基、维数
①维数: R n {\rm R}^n Rn 指n维向量空间,由n个线性无关的n维向量张成。
n维向量空间,秩为n:
①秩为n的向量组,可以表示n维向量空间中的一切向量。
②反之,若某向量组不能表示该向量空间中的某一向量,则该向量组不满秩,秩<n。
例如,3维向量空间秩为3。即任一秩为3的向量组,可以表示该向量空间中的一切向量。
若有一向量,不能被向量组 α 1 , α 2 , α 3 α_1,α_2,α_3 α1,α2,α3表示,则 r ( α 1 , α 2 , α 3 ) < 3 r(α_1,α_2,α_3)<3 r(α1,α2,α3)<3
②基:证明向量组为R3的基,只需要证明向量组中各向量线性无关
③过渡矩阵: A P = B AP=B AP=B,则 过渡矩阵 P = A − 1 B P=A^{-1}B P=A−1B
④坐标:向量 = 坐标·基

基变换、过渡矩阵

坐标变换

(2)基
向量空间的基的2个必要条件:设V为向量空间,若r个向量α1,α2,…,αr∈V,且满足
(1)α1,α2,…,αr线性无关 【证明向量组为R3的基,只需要证明向量组中各向量线性无关】
(2)V中任意向量都可由α1,α2,…,αr线性表示
则向量组α1,α2,…,αr称为向量空间V的一个基,r称为向量空间V的维数,并称V为r维向量空间
基的概念类似极大线性无关组、基础解系
若把向量空间V看作向量组,则由极大线性无关组的等价定义可知,V的基就是向量组的极大无关组,V的维数就是向量组的秩。
例题1:15年20(1)
(3)基变换的过渡矩阵
求A基到B基的过渡矩阵:(原基 右乘列变换 到新基)
A P = B AP=B AP=B,则过渡矩阵 P = A − 1 B P=A^{-1}B P=A−1B
小技巧: ( A ∣ B ) → ( E ∣ A − 1 B ) = ( E ∣ P ) (A|B)→(E|A^{-1}B)=(E|P) (A∣B)→(E∣A−1B)=(E∣P)
例题1:03年4.

分析:
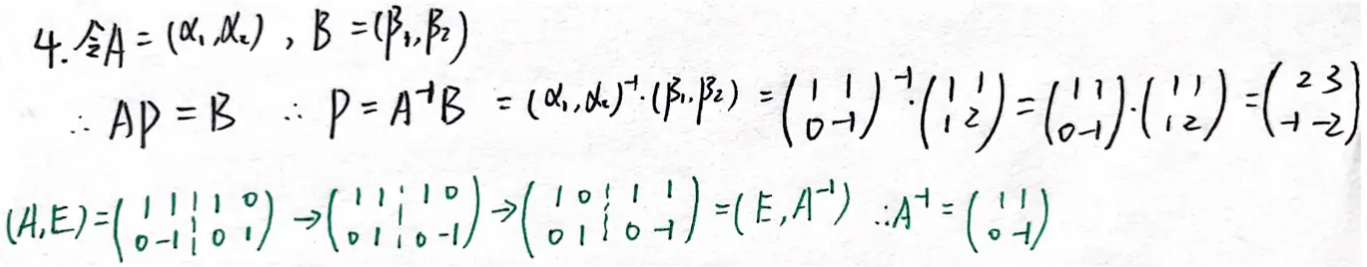
答案: ( 2 3 − 1 − 2 ) \left(\begin{array}{cc} 2 & 3 \\ -1 & -2 \end{array}\right) (2−13−2)
例题2:24李林四(四)15.

分析:

答案:
例题3:880 向量 基础填空3
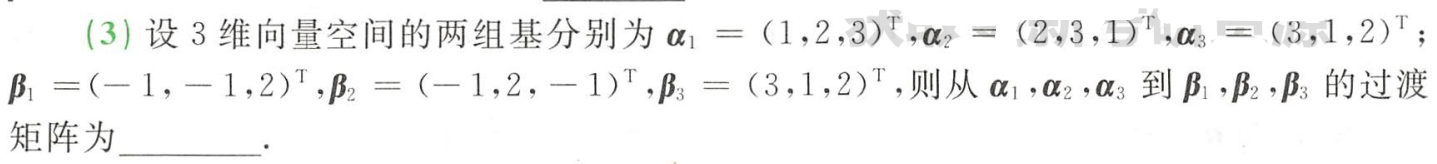
答案:
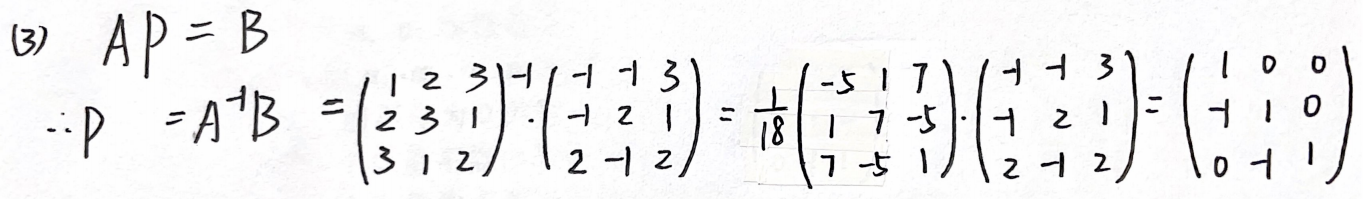
例题4:19年20.

分析:
(2)①证明3个向量是R3的基,只需证明它们线性无关 [向量的基线性无关]
②求A基到B基的过渡矩阵:
AP=B,则过渡矩阵 P=A-1B
答案:

(4)向量在基下的坐标
向量 = 坐标·基 (或 向量 = 基·坐标 )
β = ( x 1 , x 2 , x 3 ) ⋅ ( α 1 α 2 α 3 ) = x 1 α 1 + x 2 α 2 + x 3 α 3 β =(x_1,x_2,x_3)·\left(\begin{array}{c} α_1 \\ α_2 \\ α_3 \end{array}\right)=x_1α_1+x_2α_2+x_3α_3 β=(x1,x2,x3)⋅ α1α2α3 =x1α1+x2α2+x3α3
即 β = x 1 α 1 + x 2 α 2 + x 3 α 3 β =x_1α_1+x_2α_2+x_3α_3 β=x1α1+x2α2+x3α3
例题1:880 向量 基础填空2

分析:
β = x 1 α 1 + x 2 α 2 + x 3 α 3 β =x_1α_1+x_2α_2+x_3α_3 β=x1α1+x2α2+x3α3
( 2 0 0 ) = x 1 ( 1 1 0 ) + x 2 ( 1 0 1 ) + x 3 ( 0 1 1 ) = ( x 1 + x 2 x 1 + x 3 x 2 + x 3 ) \left(\begin{array}{c} 2 \\ 0 \\ 0 \end{array}\right)=x_1\left(\begin{array}{c} 1 \\ 1 \\ 0 \end{array}\right) +x_2\left(\begin{array}{c} 1 \\ 0 \\ 1 \end{array}\right)+x_3\left(\begin{array}{c} 0 \\ 1 \\ 1 \end{array}\right)=\left(\begin{array}{c} x_1+x_2 \\ x_1+x_3 \\ x_2+x_3 \end{array}\right) 200 =x1 110 +x2 101 +x3 011 = x1+x2x1+x3x2+x3
解得: x 1 = 1 , x 2 = 1 , x 3 = − 1 x_1=1,x_2=1,x_3=-1 x1=1,x2=1,x3=−1,即坐标为 ( x 1 , x 2 , x 3 ) = ( 1 , 1 , − 1 ) (x_1,x_2,x_3)=(1,1,-1) (x1,x2,x3)=(1,1,−1)
答案: ( 1 , 1 , − 1 ) (1,1,-1) (1,1,−1)
例题2:24李林六(一)15、23李林四(二)15.

分析:

答案: ( 2 2 , 2 , − 2 2 ) (\dfrac{\sqrt{2}}{2},\sqrt{2},-\dfrac{\sqrt{2}}{2}) (22,2,−22)
例题3:15年20.

分析:
(1)证明向量组是R3的一个基,只需要证明向量组线性无关
(2)坐标
5.空间直线
直线的点向式方程、直线的参数方程、向量形式、线性表示
| A的秩 | 行列式 | 三点 | l两直线 |
|---|---|---|---|
| r ( A ) = 1 r(A)=1 r(A)=1 | ∣ A ∣ = 0 \lvert A\rvert=0 ∣A∣=0 | 三点重合 | |
| r ( A ) = 2 r(A)=2 r(A)=2 | ∣ A ∣ = 0 \lvert A\rvert=0 ∣A∣=0 | 三个不同点,共线 | 两直线平行 |
| r ( A ) = 3 r(A)=3 r(A)=3 | ∣ A ∣ ≠ 0 \lvert A\rvert≠0 ∣A∣=0 | 三个不同点,不共线 | 两直线交于一点 |
例题1:20年6.

分析:两线交于一点,故它们的方向向量 α 1 ⃗ \vec{α_1} α1和 α 2 ⃗ \vec{α_2} α2 不共线,从而 α 1 ⃗ \vec{α_1} α1与 α 2 ⃗ \vec{α_2} α2线性无关。∴ α 3 α_3 α3可由 α 1 , α 2 α_1,α_2 α1,α2线性表示。由空间直线的参数式方程,得 α 3 = t α 1 + ( 1 − t ) α 2 α_3=tα_1+(1-t)α_2 α3=tα1+(1−t)α2。选C

答案:C
例题2:1998年4. |A|≠0 ⇔ \Leftrightarrow ⇔ 交于一点

分析:
r(A)=3,|A|≠0,三线相交与一点
答案:A
例题3:660 T640

分析:
r(A)=3,|A|≠0,两线相交与一点
答案:A
例题4:24李林六(六)6. r ( A ) = 2 ⇔ r(A)=2\Leftrightarrow r(A)=2⇔ 共线

分析:
r(A)=3:|A|≠0,三线交于一点
r(A)=2:|A|=0,共线
r(A)=1:|A|=0,三点重合

答案:D
例题5:24李林四(三)6.


分析:
三个不同点,则r(A)>1,排除AD
不能判断三点是否共线。若三点共线,则r(A)=2;若三点不共线,则r(A)=3
答案:C
第4章 线性方程组

(一)具体型线性方程组

1.齐次线性方程组 Ax=0
1.齐次线性方程组 A m × n x = 0 A_{m×n}x=0 Am×nx=0:m为方程个数,n为未知数个数。m<n时就有自由变量
2.齐次方程组的解x:是与系数矩阵A的行向量都正交的n维向量

例题1:880 向量 综合选择5
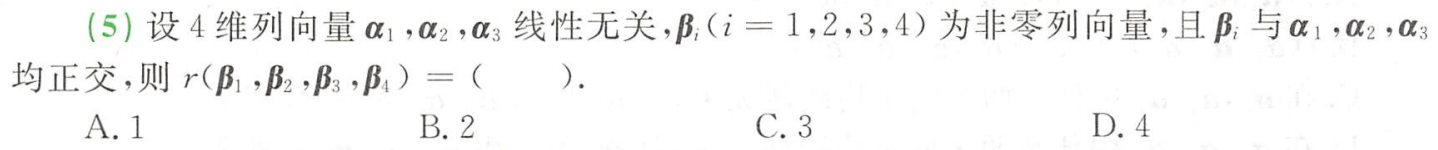
分析:
B = ( β 1 , β 2 , β 3 , β 4 ) B=(β_1,β_2,β_3,β_4) B=(β1,β2,β3,β4)与4维列向量 α 1 , α 2 , α 3 α_1,α_2,α_3 α1,α2,α3都正交,则 α 1 , α 2 , α 3 α_1,α_2,α_3 α1,α2,α3为齐次方程组 B X = 0 BX=0 BX=0的解。
∴ s = n − r ( B ) s= n-r(B) s=n−r(B),即 3 = 4 − r ( B ) 3=4-r(B) 3=4−r(B),∴ r ( B ) = r ( β 1 , β 2 , β 3 , β 4 ) = 1 r(B)=r(β_1,β_2,β_3,β_4)=1 r(B)=r(β1,β2,β3,β4)=1
答案:A
例题2:18年20.(1)
(1)有解的条件:齐次线性方程组解的判别
Am×nX=0,齐次必然有解。
① r ( A ) = n r(A)=n r(A)=n ( α 1 , α 2 , . . . , α n α_1,α_2,...,α_n α1,α2,...,αn线性无关):仅有唯一零解。
② r ( A ) < n r(A)<n r(A)<n ( α 1 , α 2 , . . . , α n α_1,α_2,...,α_n α1,α2,...,αn线性相关):零解和无穷多个非零解 。且有n-r个线性无关解 (用这n-r个线性无关解,来表示这无穷多个解) [n为矩阵A的列数,即未知数的个数]

A x = 0 Ax=0 Ax=0的无穷多解是一个“解空间”,用 k 1 ξ 1 + k 2 ξ 2 + . . . , k n − r ξ n − r k_1ξ_1+k_2ξ_2+...,k_{n-r}ξ_{n-r} k1ξ1+k2ξ2+...,kn−rξn−r表示(s=n-r)
(2)解的性质:齐次解的性质
解的叠加性:解的线性组合也是解
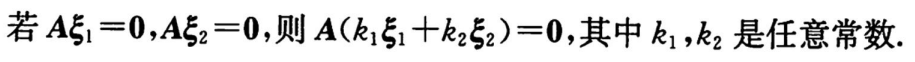
(3)基础解系、通解的结构
①基础解系
1.基础解系的定义:
设 ξ 1 , ξ 2 , . . . , ξ n − r ξ_1,ξ_2,...,ξ_{n-r} ξ1,ξ2,...,ξn−r满足
①均是方程组 A x = 0 Ax=0 Ax=0的解
②线性无关
③方程组 A x = 0 Ax=0 Ax=0的任一解向量均可由 ξ 1 , ξ 2 , . . . , ξ n − r ξ_1,ξ_2,...,ξ_{n-r} ξ1,ξ2,...,ξn−r线性表出
则称 ξ 1 , ξ 2 , . . . , ξ n − r ξ_1,ξ_2,...,ξ_{n-r} ξ1,ξ2,...,ξn−r 为 A x = 0 Ax=0 Ax=0 的一个基础解系。
基础解系是齐次方程组 A x = 0 Ax=0 Ax=0 的解向量集合的极大线性无关组。
2.基础解系的求法:见(4)求解方法与步骤的前三步
3.定理:
设A是m×n矩阵,若 r ( A ) = r < n r(A)=r<n r(A)=r<n,则齐次线性方程组 A X = 0 AX=0 AX=0 存在基础解系,并且基础解系由 n − r n-r n−r 个线性无关的解向量构成
s=n-r:基础解系中线性无关的解向量的个数 = 自由变量的个数
②通解的结构
(1)齐次
①先求出 n − r ( A ) n-r(A) n−r(A)个线性无关的基础解系
②每一个基础解系前面加一个 k i k_i ki,基础解系的线性组合即为齐次线性方程组的通解。
则齐次方程组的通解为: X = k 1 ξ 1 + k 2 ξ 2 + k 3 ξ 3 + . . . k n − r ξ n − r X=k_1ξ_1+k_2ξ_2+k_3ξ_3+...k_{n-r}ξ_{n-r} X=k1ξ1+k2ξ2+k3ξ3+...kn−rξn−r
(2)非齐次
若非齐次方程组 A X = β AX=β AX=β的特解为 β β β,则非齐次方程组的通解为: X = k 1 ξ 1 + k 2 ξ 2 + k 3 ξ 3 + . . . + . . . + k n − r ξ n − r + β X=k_1ξ_1+k_2ξ_2+k_3ξ_3+...+...+k_{n-r}ξ_{n-r}+β X=k1ξ1+k2ξ2+k3ξ3+...+...+kn−rξn−r+β
通解形成“s维解空间”,s=n-r
③自由变量
(1)谁是自由变量:化行阶梯/行最简矩阵时,不在直角边上的 x i x_i xi为自由变量
(2)自由变量/线性无关的解向量的个数: n − r ( A ) n-r(A) n−r(A)
(3)自由变量的设置:
①1个自由变量:1
②2个自由变量: ( 1 0 ) , ( 0 1 ) \binom{1}{0},\binom{0}{1} (01),(10)
③3个自由变量: ( 1 0 0 ) \left(\begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right) 100 , ( 0 1 0 ) \left(\begin{array}{c} 0 \\ 1 \\ 0 \end{array}\right) 010 , ( 0 0 1 ) \left(\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right) 001
例题1:14年20

分析:
(2)A3×4B4×3=E3×3
由于A和B都不是方阵,故AB都不可逆,更没有行列式。
考虑拆分,B=(b1,b2,b3),E=(e1,e2,e3)。则AB=E被拆成Ab1=e1,Ab2=e2,Ab3=e3
bi=kiξ+特解,k为任意常数
(4)求齐次方程组Ax=0的通解 (解齐次线性方程组)
①求基础解系
②齐次通解 = k 1 ξ 1 + k 2 ξ 2 + . . . + k n ξ n k_1ξ_1+k_2ξ_2+...+k_nξ_n k1ξ1+k2ξ2+...+knξn
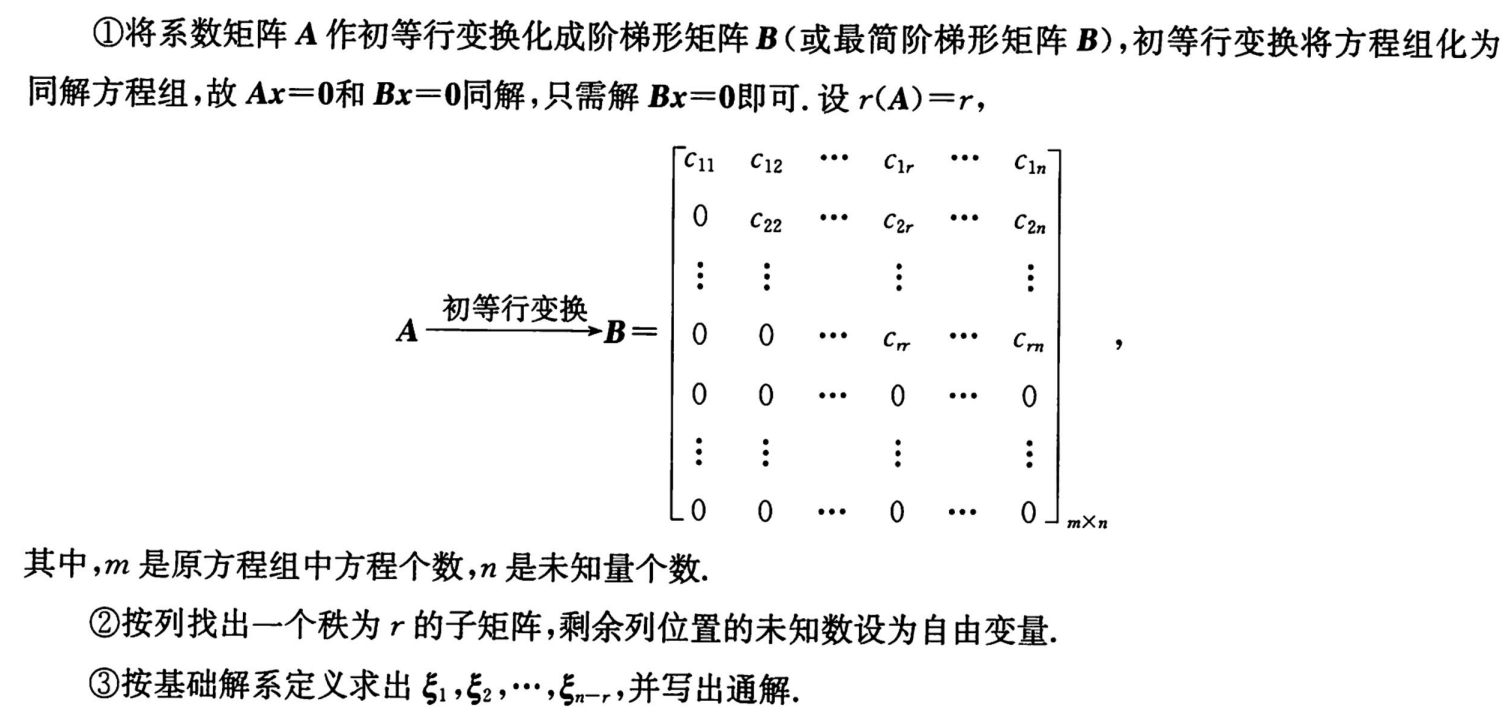
2.基础解系(前3步)、通解求法:
①把A化为行阶梯/行最简矩阵 (方程组经初等行变换转化为同解方程组)
②找出一个秩为r=r(A)的子矩阵,基础解系为s=n-r个,把n-r(A)个 x i x_i xi设为自由变量。(有同阶的才能设为自由变量)
(例如n=5,r(A)=3,s=n-r=5-3=2,基础解系有2个成员 ξ 1 , ξ 2 ξ_1,ξ_2 ξ1,ξ2
设 x 4 , x 5 x_4,x_5 x4,x5为自由变量,则 ξ 1 , ξ 2 ξ_1,ξ_2 ξ1,ξ2的最后两维:(1,0) (0,1),即 ξ 1 = ( , , 1 , 0 ) T , ξ 2 = ( , , 0 , 1 ) T ξ_1=( , , 1,0)^T,ξ_2=( , , 0,1 )^T ξ1=(,,1,0)T,ξ2=(,,0,1)T。
线性无关的解向量的个数为n-r
③根据行阶梯/行最简矩阵,由最后一行倒着开始求其余变量的值,直至第一行,求出一个解向量 ξ 1 ξ_1 ξ1;再从最后一行开始求,得到第二个解向量 ξ 2 ξ_2 ξ2;直至求完所有解向量 ξ n − r ξ_{n-r} ξn−r
④齐次线性方程组的通解为: k 1 ξ 1 + k 2 ξ 2 + . . . + k n − r ξ n − r k_1ξ_1+k_2ξ_2+...+k_{n-r}ξ_{n-r} k1ξ1+k2ξ2+...+kn−rξn−r

例题1:19年13. 解齐次线性方程组 (求齐次线性方程组的通解)
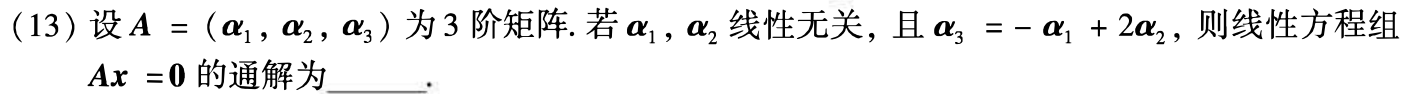
分析:

答案: k ( 1 − 2 1 ) k\left(\begin{array}{c} 1 \\ -2 \\ 1 \end{array}\right) k 1−21 ,k为任意常数
2.非齐次线性方程组 Ax=β
非齐次线性方程组 Am×nx=β,可组合成AX=B
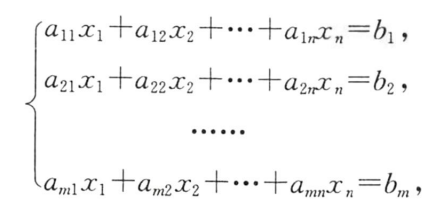
①方程组形式: A X = β AX=β AX=β
②向量形式: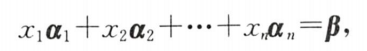
①方程组的解 x 1 , x 2 , . . . x n x_1,x_2,...x_n x1,x2,...xn,就是向量与向量之间的表示系数
②齐次线性方程组Ax=0,称为非齐次线性方程组Ax=β的导出组
(1)非齐次线性方程组有解的条件
对于 非齐次线性方程组 Ax=β:
| 秩的关系 | 线性表示 | 解的情况 |
|---|---|---|
| (1)r(A)≠r(A,β) | β不能由α₁,α₂,α₃线性表示 | 无解 |
| (2)r(A)=r(A,β) | β可由α₁,α₂,α₃线性表示 | 有解 |
| (2)①r(A)=r(A,β)=n | β可由α₁,α₂,…,αn线性表示且表示法唯一 | 有唯一解 |
| (2)②r(A)=r(A,β)<n | β可由α₁,α₂,…,αn线性表示且表示法不唯一 | 有无穷多解 |
例题1:880 线性方程组 综合选择3

分析:Ax=0有无穷多解⇦⇨ r ( A ) = r ( A ∣ b ) < n r(A)=r(A|b)<n r(A)=r(A∣b)<n
A.未提及 r ( A ) = r ( A ∣ b ) r(A)=r(A|b) r(A)=r(A∣b),不一定有解。A❌
B.Ax=0有非零解⇦⇨ r ( A ) < n r(A)<n r(A)<n,未提及 r ( A ) = r ( A ∣ b ) r(A)=r(A|b) r(A)=r(A∣b),不一定有解。B❌
D.A的列向量组线性相关⇦⇨ r ( A ) < n r(A)<n r(A)<n,未提及 r ( A ) = r ( A ∣ b ) r(A)=r(A|b) r(A)=r(A∣b),不一定有解。D❌
C.必要性:显然,有无穷解必然有两个不同解
充分性:设x1,x2为Ax=b的两个不同解,则x1-x2≠0。则A(x1-x2)=0有非零解。r(A)<n。
又∵有解,∴r(A)=r(A|b)
综上,r(A)=r(A|b)<n
答案:C
(2)解的性质:非齐次解的性质

(3)求非齐次方程组Ax=b的通解
①(A,b)化简,得方程组
②求齐次方程组Ax=0通解:令自由变量为 (1,0) (0,1)等,求出齐次方程组的基础解系,进而求齐次方程组的通解 k 1 ξ 1 + k 2 ξ 2 + . . . k n − r ξ n − r k_1ξ_1+k_2ξ_2+...k_{n-r}ξ_{n-r} k1ξ1+k2ξ2+...kn−rξn−r
③求非齐次方程组Ax=b特解:令自由变量均=0 【等式右边为自由项 β i β_i βi。从最后一行开始,代入求解,直至第一行】
④非齐通解 = 齐次通解 + 非齐次特解
例题1:880 方程组 基础解答1
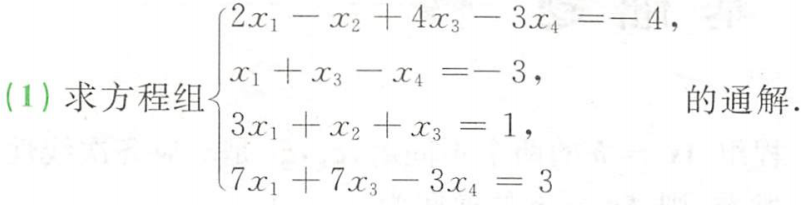
答案:

例题2:10年20.(Ⅱ) 求非齐次线性方程组的通解
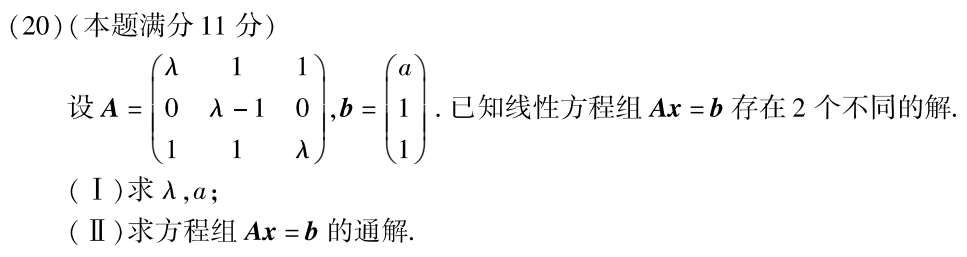
分析:
求非齐次特解:令自由变量均为0
例题3:17年20.

分析:
(Ⅱ)求解非齐次线性方程组的通解:齐次通解 + 非齐次特解
例题4:09年20.(Ⅰ) 非齐次线性方程组的求解

例题5:12年20(2)

分析:
(2)Ax=β有无穷多解,则 r ( A ) = r ( A ˉ ) < n r(A)=r(\bar{A})<n r(A)=r(Aˉ)<n,即r(A)<n,即 |A|=0
化为行最简后,先求齐次解Ax=0得基础解系ξ=(1,1,1,1)T。特解即为此时的β’=(0,-1,0,0)T。通解X=kξ+β’=k(1,1,1,1)T+(0,-1,0,0)T,k为任意常数
例题6:13年20.

分析:设 C = ( x 1 x 2 x 3 x 4 ) C=\left(\begin{array}{cc} x_1 & x_2 \\ x_3 & x_4 \end{array}\right) C=(x1x3x2x4),由AC-CA=B得出含x的方程组,写为系数矩阵D的增广矩阵 D ˉ \bar{D} Dˉ,化为行最简矩阵。这时就可以通过非齐次线性方程组解的判别条件 r ( D ) = r ( D ˉ ) r(D)=r(\bar{D}) r(D)=r(Dˉ)来求a,b的值了。求出后把a,b代入 D ˉ \bar{D} Dˉ,求出齐次方程组的基础解析 ξ 1 = ( 1 − 1 1 0 ) ξ_1=\left(\begin{array}{c} 1 \\ -1 \\ 1 \\ 0 \end{array}\right) ξ1= 1−110 , ξ 2 = ( 1 0 0 1 ) ξ_2=\left(\begin{array}{c} 1 \\ 0 \\ 0 \\ 1 \end{array}\right) ξ2= 1001 ,非齐次通解X= ( x 1 x 2 x 3 x 4 ) = k 1 ξ 1 + k 2 ξ 2 + ( 1 0 0 0 ) \left(\begin{array}{c} x_1 \\ x_2 \\ x_3 \\ x_4 \end{array}\right)=k_1ξ_1+k_2ξ_2+\left(\begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \end{array}\right) x1x2x3x4 =k1ξ1+k2ξ2+ 1000
∴ C = ( x 1 x 2 x 3 x 4 ) C=\left(\begin{array}{cc} x_1 & x_2 \\ x_3 & x_4 \end{array}\right) C=(x1x3x2x4)=…
例题7:23李林六套卷(二)15.
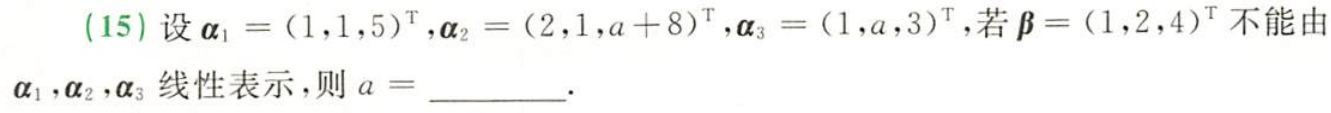
分析:β不能由α₁,α₂,α₃线性表示,即非齐次线性方程组无解, r ( A ) ≠ r ( A , β ) r(A)≠r(A,β) r(A)=r(A,β)

答案:0
例题8:880 方程组 基础解答2 含参方程组

分析:
含参方程组:若A为n×n方阵,先令|A|=0,求出参数。不为参数时,|A|≠0,有唯一解。|A|=0时,无穷多解或无解。
答案:

例题9:880 方程组 基础解答7 凑

答案:

例题10:880 方程组 基础解答6 A 11 ≠ 0 A_{11}≠0 A11=0,则 r ( A ) ≥ n − 1 r(A)≥n-1 r(A)≥n−1

答案:
解法一(李林):

解法2(喻老):
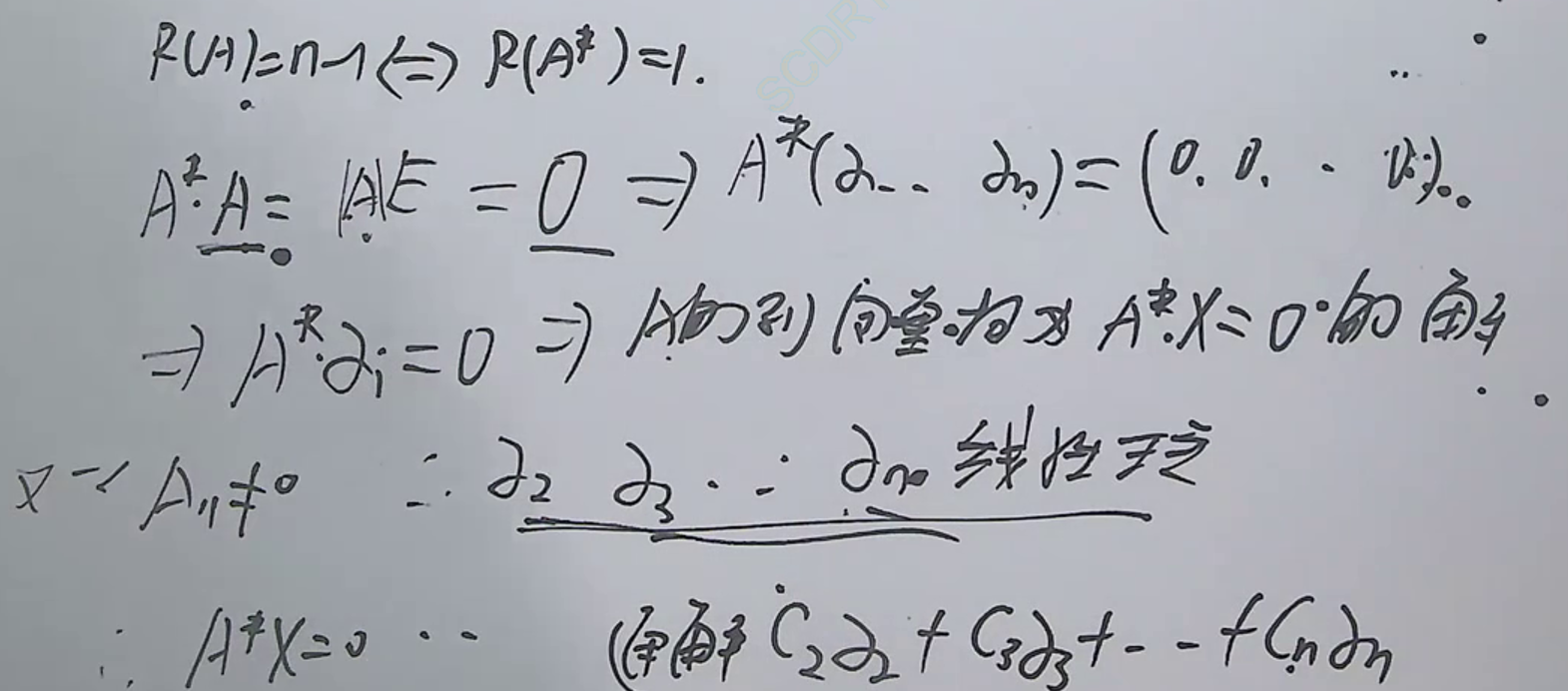
例题11:880 方程组 综合解答1 用非齐次的解,代入+组合,凑出齐次的解

答案:

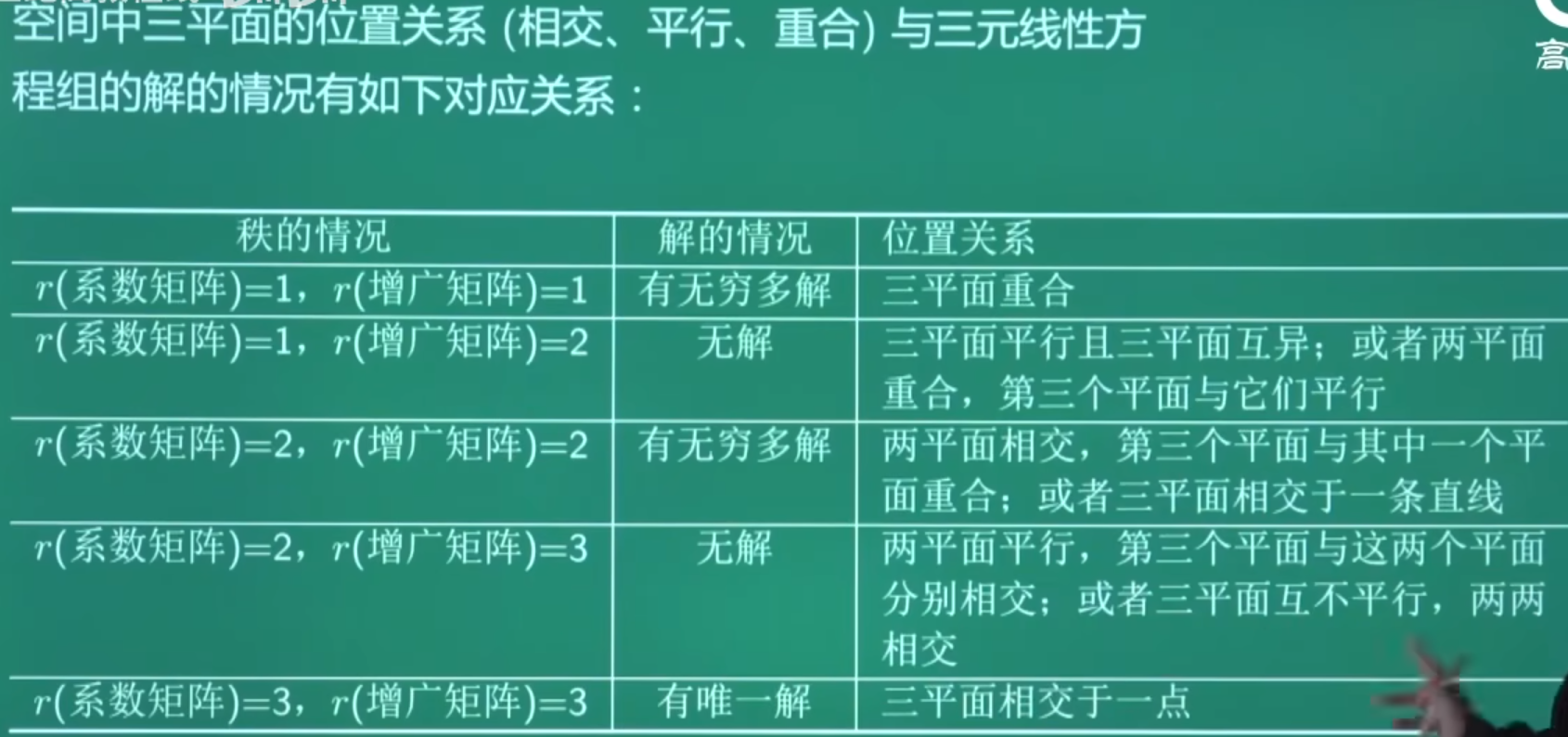
(4)非齐次线性方程组的几何意义
(1) 3个方程代表3个平面,三平面共同交点个数代表方程组解的个数
① r ( A ) = r ( A ˉ ) = 1 r(A)=r(\bar{A})=1 r(A)=r(Aˉ)=1:三个平面重合
② r ( A ) = r ( A ˉ ) = 2 r(A)=r(\bar{A})=2 r(A)=r(Aˉ)=2:三个平面交于一条直线
③ r ( A ) = r ( A ˉ ) = 3 r(A)=r(\bar{A})=3 r(A)=r(Aˉ)=3:三个平面交于一点
④ r ( A ) = 2 , r ( A ˉ ) = 3 r(A)=2,r(\bar{A})=3 r(A)=2,r(Aˉ)=3:两两平面交于一条直线,三平面无共同交点
(2) 3个方程代表3条直线,交点代表解的个数

平面互异:不重合
例题1:02年10. 系数矩阵秩、增广矩阵秩 用空间中的平面表示
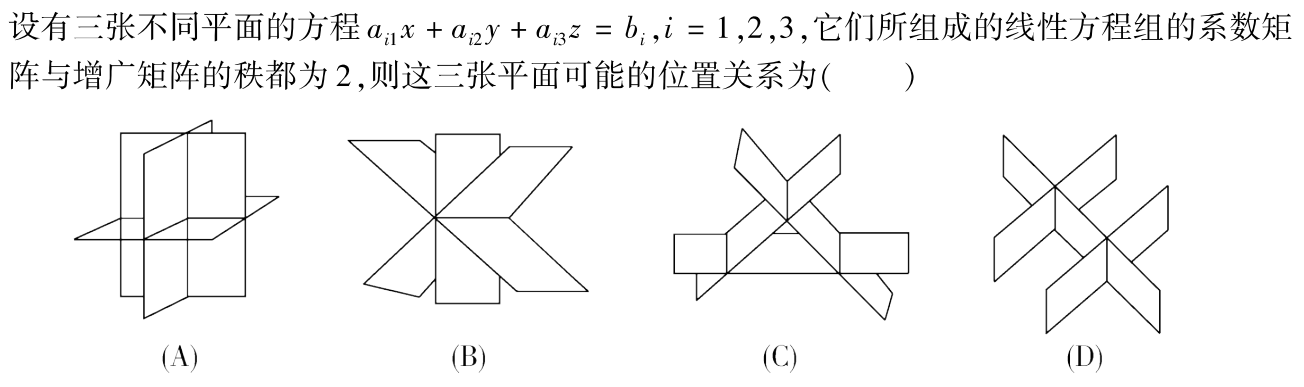
分析:
A.三个平面只有一个交点,方程组有唯一解, r ( A ) = r ( A ˉ ) = 3 r(A)=r(\bar{A})=3 r(A)=r(Aˉ)=3。A❌
B.三个平面相较于同一条直线,即方程组有无穷多个解, r ( A ) = r ( A ˉ ) = 2 < 3 r(A)=r(\bar{A})=2<3 r(A)=r(Aˉ)=2<3。B✔
C.两两相交,互不平行: r ( A ) = 2 , r ( A ˉ ) = 3 r(A)=2,r(\bar{A})=3 r(A)=2,r(Aˉ)=3。 C❌
D.两平面平行,第三个平面与这两个平行平面分别相交: r ( A ) = 2 , r ( A ˉ ) = 3 r(A)=2,r(\bar{A})=3 r(A)=2,r(Aˉ)=3。D❌
答案:B
例题2:19年6.

分析:
两两相交,互不平行: r ( A ) = 2 , r ( A ˉ ) = 3 r(A)=2,r(\bar{A})=3 r(A)=2,r(Aˉ)=3
答案:A
例题3:880 方程组 综合选择4

分析:三平面交于一条直线,有解且有无穷多解,r(A)=r(A|b)<n。排除BC。
D的情况,r(A)=r(A|b)=1是三平面重合。
答案:A
例题4:23李林六套卷(三)7.

分析:3个平面相较于一条直线,则有无穷多个交点,则 r ( A ) = r ( A ˉ ) < 3 r(A)=r(\bar{A})<3 r(A)=r(Aˉ)<3
A ˉ = ( 1 1 b ∣ 3 2 a + 1 b + 1 ∣ 7 0 1 − a 2 b − 1 ∣ 0 ) \bar{A}=\left(\begin{array}{cc} 1 & 1 & b &| \ 3 \\ 2 & a+1 & b+1 &| \ 7 \\ 0 & 1-a & 2b-1 &| \ 0\\ \end{array}\right) Aˉ= 1201a+11−abb+12b−1∣ 3∣ 7∣ 0
显然,第三行要为全0,则a=1,b=1/2
答案:B
例题5:
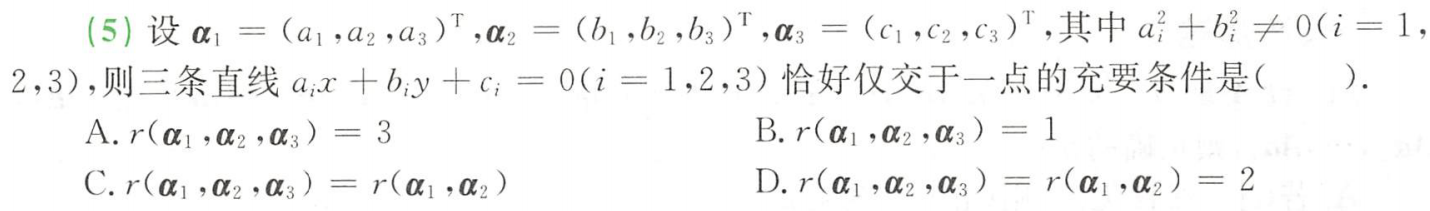
分析:

答案:D
3.矩阵方程 AX=B
解矩阵方程AX=B:
将(A,B)化为行最简 (A’,B’),则AX=B等价于A’X=B’。
求方程组A’x=0的基础解系、通解 x₁ x₂ x₃,则X = (x₁ x₂ x₃)
若解AP=B,要求P可逆,则求|P|≠0,对k₁ k₂ k₃做出限制
例题1:18年21.

分析:
(Ⅰ)矩阵A可经初等列变换化为矩阵B ⇦⇨ 列向量组等价 ⇦⇨ 矩阵方程AX=B有解 ⇦⇨ r(A)=r(A,B)
(Ⅱ)解矩阵方程AX=B:
将(A,B)化为行最简 (A’,B’),则AX=B等价于A’X=B’。
求方程组A’x=0的基础解系、通解 x₁ x₂ x₃,则X = (x₁ x₂ x₃)
若解AP=B,要求P可逆,则求|P|≠0,对k₁ k₂ k₃做出限制
答案:

(二)抽象型线性方程组



4.解就是系数

例题1:基础30讲线代分册 求非齐次线性方程组的通解、解的性质

分析:
①非齐通的解结构:非齐通 = 齐通 + 非齐特
②解的性质:i. η 1 − η 2 η_1-η_2 η1−η2为齐次特解 ii. 1 2 ( η 1 + η 2 ) \dfrac{1}{2}(η_1+η_2) 21(η1+η2)为非齐次特解, 1 3 ( η 3 + 2 η 2 ) \dfrac{1}{3}(η_3+2η_2) 31(η3+2η2)为非齐次特解 iii. 1 2 ( η 1 + η 2 ) − 1 3 ( η 3 + 2 η 2 ) \dfrac{1}{2}(η_1+η_2)-\dfrac{1}{3}(η_3+2η_2) 21(η1+η2)−31(η3+2η2)也为齐次通解,乘6倍后 3 ( η 1 + η 2 ) − 2 ( η 3 + 2 η 2 ) 3(η_1+η_2)-2(η_3+2η_2) 3(η1+η2)−2(η3+2η2)仍为齐次通解
本题不必求出 η 1 , η 2 , η 3 η_1,η_2,η_3 η1,η2,η3各自的值
答案:
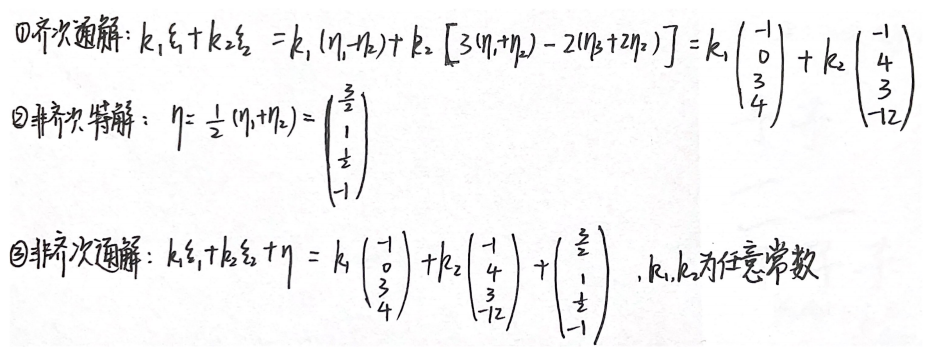
例题2:
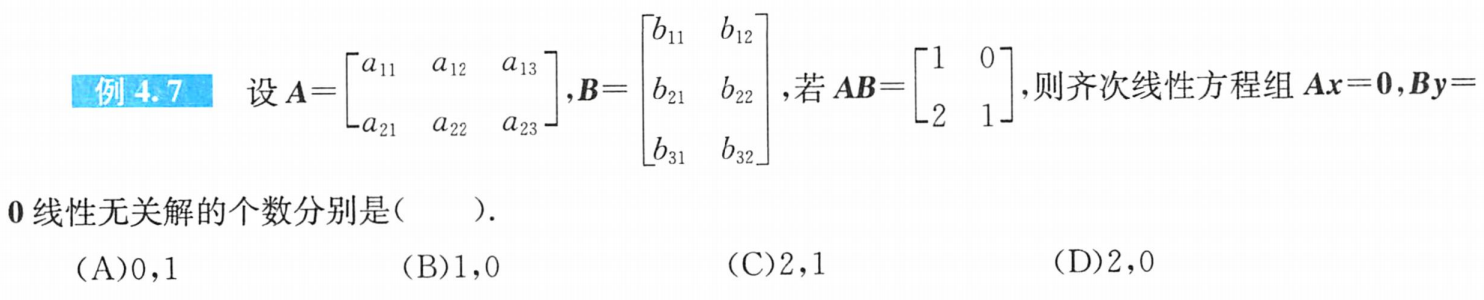
分析:
① r ( A B ) ≤ m i n { r ( A ) , r ( B ) } r(AB)≤min\{ r(A),r(B)\} r(AB)≤min{r(A),r(B)}:由题得r(AB)=2≤min{ r(A),r(B} ∴r(A)≥2,r(B)≥2
又∵秩=行秩=列秩≤min{m,n},∴r(A)≤2,r(B)≤2
故r(A)=r(B)=2
②线性无关解的个数 s = n − r s=n-r s=n−r
s A = n A − r ( A ) = 3 − 2 = 1 s_A=n_A-r(A)=3-2=1 sA=nA−r(A)=3−2=1
s B = n B − r ( B ) = 2 − 2 = 0 s_B=n_B-r(B)=2-2=0 sB=nB−r(B)=2−2=0
答案:B
例题3:

分析:
①s=n-r(A)=1 ∴r(A)=3 ∴r(A*)=1 ∴s*=n-r(A*)=3 排除AB
②(1,0,1,0)T是Ax=0的一个基础解系(其中A=(α₁,α₂,α₃,α₄)),即α₁+α₃=0,即α₁与α₃能相互线性表示,线性相关。故A*x=0的基础解系只能选 124或234。选D
答案:D
例题4:

答案:

(三)方程组的公共解、同解方程组
1.方程组的公共解
齐次线性方程组 A m × n x = 0 A_{m×n}x=0 Am×nx=0和 B m × n x = 0 B_{m×n}x=0 Bm×nx=0的公共解:
①A、B都是具体的方程组:
联立方程组 ( A B ) x = 0 \dbinom{A}{B}x=0 (BA)x=0的解
②A给了具体方程组,B给了基础解系:
利用基础解系求出B的通解,代入A。
③A、B都给的基础解系:
增加约束,使其相等:令 k 1 ξ 1 + k 2 ξ 2 = l 1 η 1 + l 2 η 2 k_1ξ_1+k_2ξ_2=l_1η_1+l_2η_2 k1ξ1+k2ξ2=l1η1+l2η2,找到k1k2关系,将二维解空间化为一维解空间

例题1:880 方程组 基础解答3(Ⅱ) ①A、B都是具体的方程组:联立方程组

例题2:880 方程组 基础解答4 ②A给了具体方程组,B给了基础解系:通解代入具体方程组
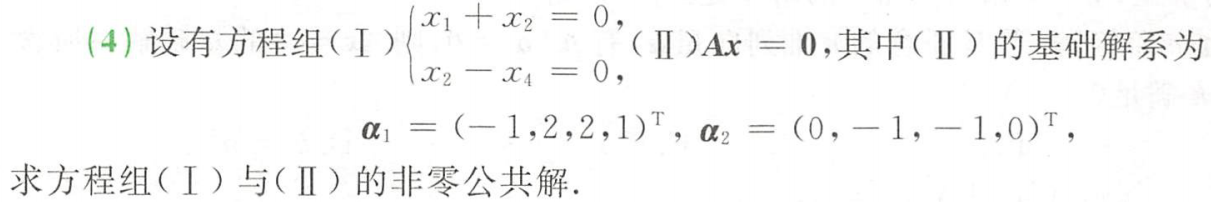
答案:

2.同解方程组
1.定义/概念:两个方程组 A m × n x = 0 A_{m×n}x=0 Am×nx=0 和 B m × n x = 0 B_{m×n}x=0 Bm×nx=0 有完全相同的解,则称它们为同解方程组
2.性质:
A x = 0 Ax=0 Ax=0 与 B x = 0 Bx=0 Bx=0 为同解方程组 (方程组 A x = 0 Ax=0 Ax=0与 B x = 0 Bx=0 Bx=0 同解)
⇦⇨A与B的行向量组为等价向量组 (行向量组等价),A能通过初等行变换得到B,B也能通过初等行变换得到A
⇦⇨ r ( A ) = r ( B ) = r ( A B ) r(A)=r(B)=r\dbinom{A}{B} r(A)=r(B)=r(BA)
⇦⇨有完全相同的解:即Ax=0的解满足Bx=0,且Bx=0的解满足Ax=0 (互相把解代入,求出结果即可)
⇦⇨可相互线性表示:Ⅱ增广矩阵的行向量能被Ⅰ增广矩阵的行向量线性表示,反之亦然。
行向量组等价:是指两个行向量组所生成的向量空间相同,即它们具有相同解集。即一个行向量组可以通过一系列初等行变换变为另一个行向量组,那么称这两个行向量组等价
例题1:20年5. 初等列变换、同解方程组

分析:
(1)左乘行变换,右乘列变换。A能通过初等列变换得到B,则B一定也能通过初等列变换得到A。即选B
(2)Ax=0与Bx=0是同解方程组,即A与B的行向量组等价,即A能通过初等行变换得到B,B也能通过初等行变换得到A
答案:B
例题2:22年6.

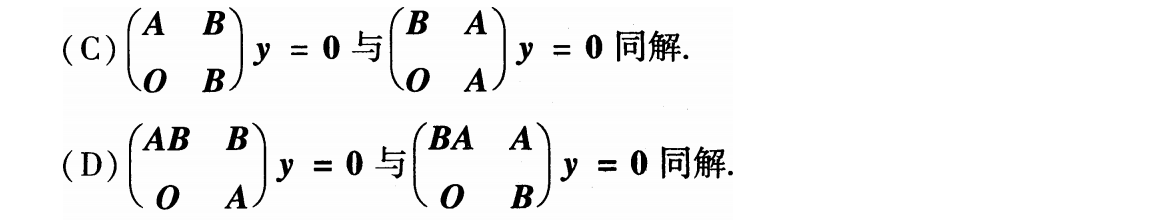
分析:
①仅有零解 ⇦⇨ 系数矩阵满秩
②齐次方程组的同解变形 ⇦⇨ 矩阵的初等行变换

答案:C
例题3:同解方程组

例题4:设Am×n,证明r(A)=r(ATA)

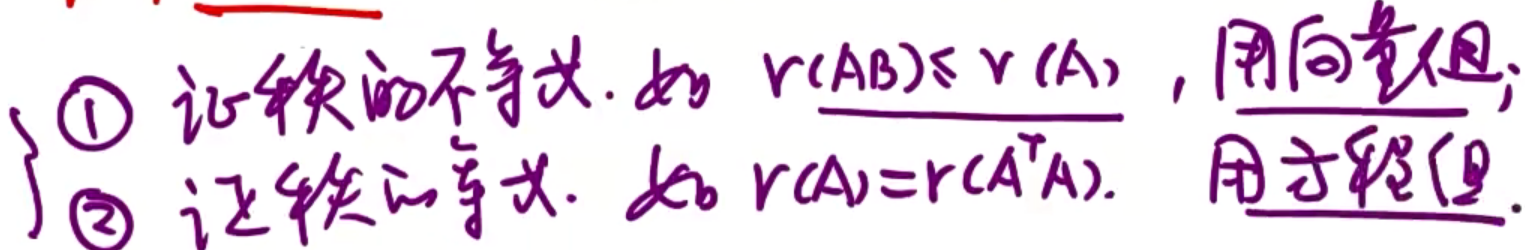
证明:

∴r(A)=r(AT)=r(ATA)=r(AAT),对任意Am×n均成立
这篇关于线性代数(主题篇):Ch3.向量组 、Ch4.方程组的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!