本文主要是介绍基于ESTAR指数平滑转换自回归模型的CPI数据统计分析matlab仿真,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1.程序功能描述
2.测试软件版本以及运行结果展示
3.核心程序
4.本算法原理
4.1 ESTAR模型概述
4.2 WNL值,P值, Q值,12阶ARCH值
4.3ADF检验
5.完整程序
1.程序功能描述
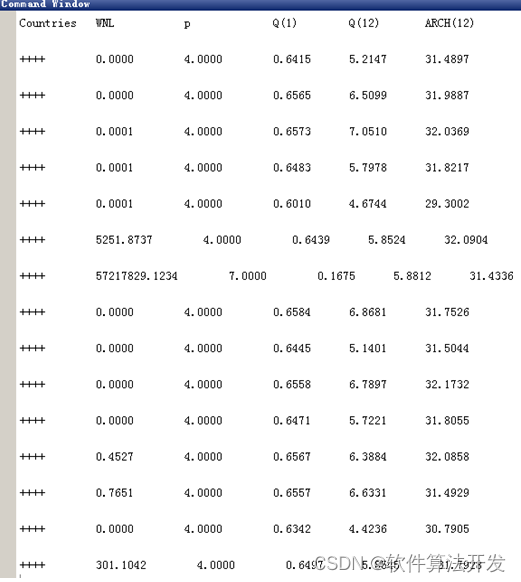
基于ESTAR指数平滑转换自回归模型的CPI数据统计分析matlab仿真.主要通过M-ESTAR模型进行计算,主要涉及到的统计量有WNL值,P值, Q值,12阶ARCH值。
2.测试软件版本以及运行结果展示
MATLAB2022a版本运行

3.核心程序
....................................................................
%%
%调用模型ESTAR
for i = 1:length(Real_exchange_rate)i[y,th] = func_MESTAR2(Real_exchange_rate{i});Real_exchange_rate_ESTAR{i} = y;%估计得到的thetatheta{i} = th(end);
endk = [-1 -1 -0.3 -0.3 -0.3 -0.3 -1 -0.3 -0.3 -0.3 -0.3 -0.3 -1 -0.3 -0.3];
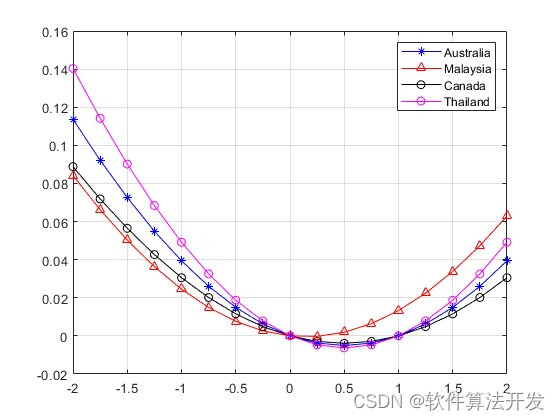
for i = 1:length(Real_exchange_rate)tmps = -2:0.25:2;for j = 1:length(tmps) T{i}(j) = 1-exp(-(theta{i}*tmps(j)^2 + theta{i}*k(i)*tmps(j)));end
endfigure;
plot(tmps,T{1},'b-*');hold on
plot(tmps,T{8},'r-^');hold on
plot(tmps,T{2},'k-o');hold on
plot(tmps,T{13},'m-o');hold on
grid on
legend('Australia','Malaysia','Canada','Thailand');figure;
plot(tmps,T{9},'b-*');hold on
plot(tmps,T{10},'r-^');hold on
plot(tmps,T{4},'k-o');hold on
plot(tmps,T{14},'m-o');hold on plot(tmps,T{5},'g-^');hold on
plot(tmps,T{11},'y-o');hold on
plot(tmps,T{3},'k-*');hold on grid on
legend('NewZealand','Singapore','Denmark','UnitedKingdom','HongKong','Switzerland','China');%计算Q(1)
for i = 1:length(Real_exchange_rate)s = func_Ljung_Box(Real_exchange_rate_ESTAR{i},1); Q1{i} = s;
end
%计算Q(12)
for i = 1:length(Real_exchange_rate)s = func_Ljung_Box(Real_exchange_rate_ESTAR{i},12); Q12{i} = s;
end%%
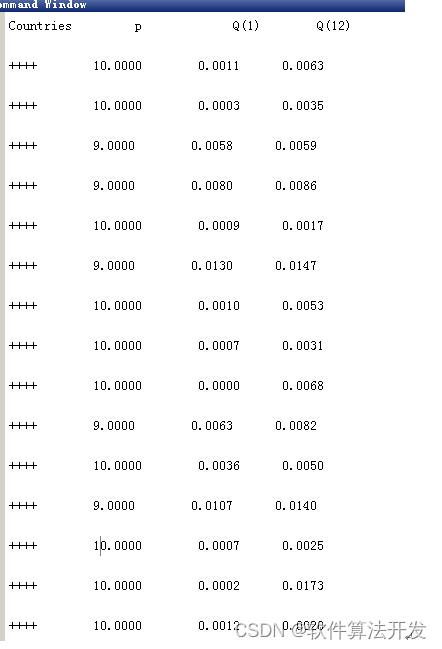
%显示诸如Table2一样的表格数据
fprintf('Countries theta Q(1) Q(12) \n\n');
for i = 1:15if i == 1fprintf('Australia ');endif i == 2fprintf('Canada ');end if i == 3fprintf('China ');end if i == 4fprintf('Denmark ');end if i == 5 fprintf('HongKong ');end if i == 6fprintf('Japan ');endif i == 7fprintf('SouthKorea ');end if i == 8fprintf('Malaysia ');end if i == 9fprintf('NewZealand ');end if i == 10fprintf('Singapore ');end if i == 11fprintf('Switzerland ');endif i == 12fprintf('Taiwan ');end if i == 13fprintf('Thailand ');end if i == 14fprintf('UnitedKingdom ');end if i == 15fprintf('issue ');end fprintf('%3.4f ',theta{i});fprintf('%3.4f ',Q1{i}); fprintf('%3.4f ',Q12{i}); fprintf('\n\n');
end
16_014m4.本算法原理
4.1 ESTAR模型概述
ESTAR(Exponential Smooth Transition AutoRegressive model)是一种混合时间序列模型,它结合了指数平滑法和状态转换自回归模型的特点。在经济数据分析中,尤其是处理诸如CPI(消费者物价指数)这类具有可能的非线性趋势变化以及结构突变的数据时,ESTAR模型具有很强的应用价值。它能够捕捉到数据中的长期趋势、季节性变动以及潜在的平滑过渡现象。
一个简单的ESTAR模型可以表示为:
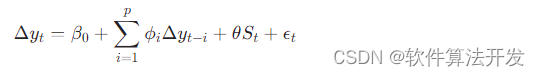

状态变量St 通常通过如下方式定义,包含两个状态(例如常态和平稳期)并允许平滑地在两者间过渡:
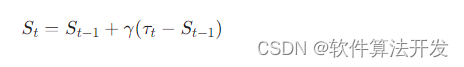
其中,
St 在 [0, 1] 区间内取值,代表从一种状态向另一种状态的转换程度。
γ 是转换速度参数,决定着状态转换的快慢。
τt 是转移函数,它是一个关于某些解释变量(如时间变量或其他宏观经济指标)的单调递增函数,当这些变量达到某个阈值时会触发状态的转变。
4.2 WNL值,P值, Q值,12阶ARCH值

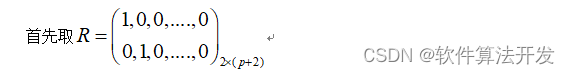


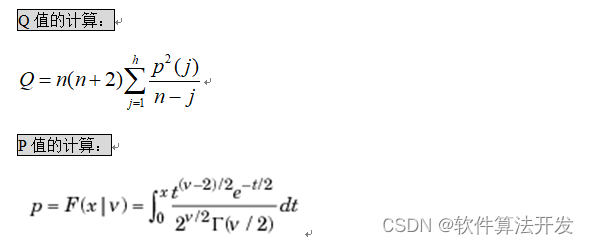
4.3ADF检验
ADF检验是增项DF检验,DF检验用于检验变量的非平稳性。若时间序列模型中含有单位根,则模型是非平稳的。对于AR(1)自回归滞后一阶模型,滞后期系数如果等于1,则无法收敛。DF检验的原假设为H0:beta=1,H1:beta<1。其中beta可以用OLS去估计。t=(beta-1)/std(beta)。t统计量并不服从t分布,而是服从DF分布。DF分布是Dickey Fuller研究的专门检验单位根的分布,DF检验是左单侧检验,当计算的t高于临界值则接受原假设(此模型是非平稳的),若t小于临界值,则拒绝原假设(此模型是平稳的)。
增项DF检验简称(ADF)用于更为复杂的模型,当模型AR(p)高阶自回归,或者带有截距项以及趋势项的时候,需要做差分ADF检验。检验是一般是三个基准模型:a:AR(1),b:AR(1)再加截距,c:b的基础上再加趋势。一般先从c开始单位根检验,当确定不含有趋势后,继续用b检验,若存在单位根,继续用a检验。当然在这个过程中如果发现不存在单位根,则检验结束。如果检验的c模型仍然不能拒绝存在单位根,则进行一阶差分后再检验,如果仍然存在单位根,再差分……直到拒绝单位根为止。根据模型的选定,分别查ADF分布表,对应临界值判断是否存在单位根。在ADF检验中,由于做了差分,通常的原假设是系数=0,因此t统计量服从t分布,可以通过回归的t值来和ADF分布进行对比。在计量软件Eviews中,unit root test选项可以根据研究的需要直接进行ADF检验。
5.完整程序
VVV
这篇关于基于ESTAR指数平滑转换自回归模型的CPI数据统计分析matlab仿真的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




