本文主要是介绍9.12零钱兑换(LC518-M)(开始完全背包,与01背包的不同仅在于遍历顺序),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!


算法:
这是一道典型的背包问题,一看到钱币数量不限,就知道这是一个完全背包。
但本题和纯完全背包不一样,纯完全背包是凑成背包最大价值是多少,而本题是要求凑成总金额的物品组合个数!
动规五步曲:
1.确定dp数组以及下标:
dp[j]:凑成总金额j的货币组合数为dp[j]
2.确定dp公式
dp[j] 就是所有的dp[j - coins[i]](考虑coins[i]的情况)相加。
dp[j] += dp[j - coins[i]];
求装满背包有几种方法,公式都是:dp[j] += dp[j - nums[i]];
3.dp数组初始化
组合-累加-dp[0]=1,一定不能为0
首先dp[0]一定要为1,dp[0] = 1是 递归公式的基础。如果dp[0] = 0 的话,后面所有推导出来的值都是0了。
下标非0的dp[j]初始化为0,这样累计加dp[j - coins[i]]的时候才不会影响真正的dp[j]
4.确定遍历顺序
对于普通的完全背包问题:完全背包的两个for循环的先后顺序都是可以的。
但本题就不行了!
因为纯完全背包求得装满背包的最大价值是多少,和凑成总和的元素有没有顺序没关系,即:有顺序也行,没有顺序也行!
本题要求凑成总和的组合数,元素之间明确要求没有顺序。
本题是求凑出来的方案个数,且每个方案个数是为组合数。
那么本题,两个for循环的先后顺序可就有说法了。
我们先来看 外层for循环遍历物品(钱币),内层for遍历背包(金钱总额)的情况。
假设:coins[0] = 1,coins[1] = 5。
for (int i = 0; i < coins.size(); i++) { // 遍历物品for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量dp[j] += dp[j - coins[i]];}
}那么就是先把1加入计算,然后再把5加入计算,得到的方法数量只有{1, 5}这种情况。而不会出现{5, 1}的情况。
所以这种遍历顺序中dp[j]里计算的是组合数!
如果把两个for交换顺序,代码如下:
for (int j = 0; j <= amount; j++) { // 遍历背包容量for (int i = 0; i < coins.size(); i++) { // 遍历物品if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];}
}背包容量的每一个值,都是经过 1 和 5 的计算,包含了{1, 5} 和 {5, 1}两种情况。
此时dp[j]里算出来的就是排列数!
5.举例推导dp数组
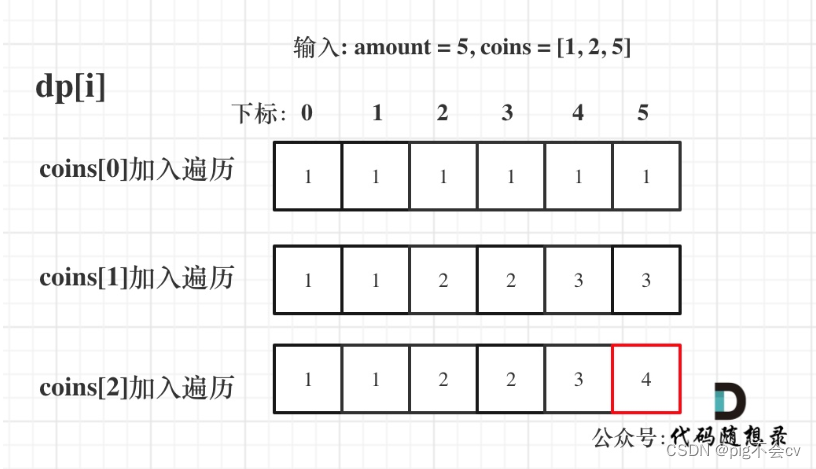
coins.size=3,amount=5
i=0:
j=coins[0]=1;j<=5;j++{
- j=1:dp[1]=dp[1-1]+dp[1]=0+1=1
- j=2:dp[2]=dp[1]+dp[2]=1+0=1
- 。
- 。
- 。
- j=5 dp[5]=dp[4]+dp[5]=1+0=1}
i=1:
j=coins[1]=2;j<=5;j++{
j=2:dp[2]=dp[2]+dp[2-2]=1+1=2
j=3:dp[3]=dp[3]+dp[1]=1+1=2
。。。。}
正确代码:
class Solution {public int change(int amount, int[] coins) {int[] dp = new int [amount+1];dp[0] = 1;//其他dp值(除了0以外的),dp[i]=0for(int i=0; i<coins.length; i++){for(int j=coins[i]; j<=amount; j++){dp[j] += dp[j-coins[i]];}}return dp[amount];}
}注意:
dp[0]=1,dp[i]=0(i !=0)
//初始化dp数组,表示金额为0时只有一种情况,也就是什么都不装dp[0] = 1;时间空间复杂度:
- 时间复杂度: O(mn),其中 m 是amount,n 是 coins 的长度
- 空间复杂度: O(m)
这篇关于9.12零钱兑换(LC518-M)(开始完全背包,与01背包的不同仅在于遍历顺序)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




