本文主要是介绍【自动驾驶坐标系基础】Frenet坐标系和Cartesian坐标系的相互转换,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Frenet坐标系和Cartesian坐标系的相互转换
2023.12.12
1 变量含义
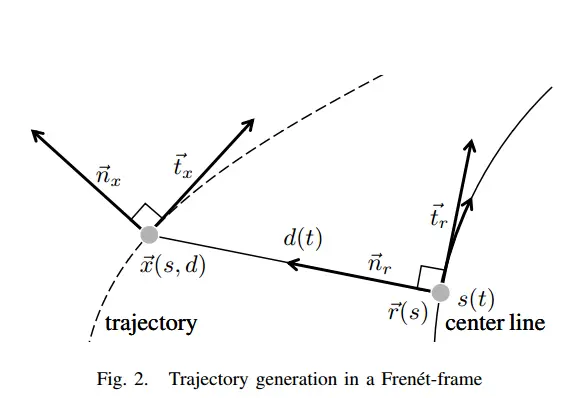
-
Frenet和Cartesian相互转换即 [ s , s ˙ , s ¨ , d , d ˙ , d ¨ ] ↔ [ X , θ x , κ x , v x , a x ] [s,\dot{s},\ddot{s},d,\dot{d},\ddot{d}] \leftrightarrow[\boldsymbol{X},\theta_x,\kappa_x,v_x,a_x] [s,s˙,s¨,d,d˙,d¨]↔[X,θx,κx,vx,ax]
-
还要用到的中间变量有 n x , t x , n r , t r , r , d ′ , d ′ ′ , θ r , Δ θ , κ r , κ x ′ , κ r ′ \boldsymbol{n_x},\boldsymbol{t_x},\boldsymbol{n_r},\boldsymbol{t_r},\boldsymbol{r},d',d'',\theta_r,\Delta\theta,\kappa_r,\kappa_x',\kappa_r' nx,tx,nr,tr,r,d′,d′′,θr,Δθ,κr,κx′,κr′
-
各变量含义:
变量 含义 X \boldsymbol{X} X Cartesian坐标系下的坐标( X = [ x , y ] \boldsymbol{X}=[x,y] X=[x,y]) r \boldsymbol{r} r trajectory上的点 X \boldsymbol{X} X对应center line上最近点的Cartesian坐标 v x , a x v_x,a_x vx,ax Cartesian坐标系下的速度和加速度 s , s ˙ , s ¨ s,\dot{s},\ddot{s} s,s˙,s¨ Frenet坐标系下的纵向坐标及其对时间的高阶导( d d t \frac{d}{dt} dtd) s x s_x sx trajectory的弧长(注:centerline弧长 s r s_r sr默认写成 s s s) d , d ˙ , d ¨ d,\dot{d},\ddot{d} d,d˙,d¨ Frenet坐标系下的横向坐标及其对时间的高阶导( d d t \frac{d}{dt} dtd) d ′ , d ′ ′ d',d'' d′,d′′ Frenet坐标系下的横向坐标对纵向坐标的高阶导( d d s \frac{d}{ds} dsd) θ x , θ r \theta_x,\theta_r θx,θr Cartesian坐标系下trajectory/center line的切线与x轴的夹角 θ r ′ \theta_r' θr′ θ r ′ = d θ r d s r = κ r \theta_r'=\frac{d\theta_r}{ds_r}=\kappa_r θr′=dsrdθr=κr Δ θ \Delta\theta Δθ Δ θ = θ x − θ r \Delta\theta = \theta_x - \theta_r Δθ=θx−θr n x , t x \boldsymbol{n_x},\boldsymbol{t_x} nx,tx Cartesian坐标系下trajectory的法线和切线
n x = [ − s i n θ x , c o s θ x ] T \boldsymbol{n_x}=[-sin{\theta_x},cos{\theta_x}]^T nx=[−sinθx,cosθx]T
t x = [ c o s θ x , s i n θ x ] T \boldsymbol{t_x}=[cos{\theta_x},sin{\theta_x}]^T tx=[cosθx,sinθx]Tn r , t r \boldsymbol{n_r},\boldsymbol{t_r} nr,tr Cartesian坐标系下center line的法线和切线
n r = [ − s i n θ r , c o s θ r ] T \boldsymbol{n_r}=[-sin{\theta_r},cos{\theta_r}]^T nr=[−sinθr,cosθr]T
t r = [ c o s θ r , s i n θ r ] T \boldsymbol{t_r}=[cos{\theta_r},sin{\theta_r}]^T tr=[cosθr,sinθr]Tκ x , κ r \kappa_x,\kappa_r κx,κr Cartesian坐标系下trajectory/center line的曲率 κ x ′ , κ r ′ \kappa_x',\kappa_r' κx′,κr′ Cartesian坐标系下trajectory/center line的曲率对纵向坐标的导数( d d s \frac{d}{ds} dsd)
2 推导
先来推导 d ˙ \dot{d} d˙,由图像容易看出, d = ( x − r ) T n r d=(\boldsymbol{x}-\boldsymbol{r})^T\boldsymbol{n_r} d=(x−r)Tnr,两边对t求导得:
d ˙ = [ x ˙ − r ˙ ] T n r + [ x − r ] T n ˙ r \dot{d}=[\dot{x}-\dot{r}]^T\boldsymbol{n}_r+[x-r]^T\dot{\boldsymbol{n}}_r d˙=[x˙−r˙]Tnr+[x−r]Tn˙r
x ˙ \dot{x} x˙很直观, x ˙ = v x t x \dot{x}=v_x\boldsymbol{t_x} x˙=vxtx,由[变化量很小时,弧长=割线=切线]的思想, r ˙ = s ˙ t r \dot{r}=\dot{s}\boldsymbol{t_r} r˙=s˙tr,最难求的是 n ˙ r \dot{\boldsymbol{n}}_r n˙r,由于 n r = [ − s i n θ r , c o s θ r ] T \boldsymbol{n_r}=[-sin{\theta_r},cos{\theta_r}]^T nr=[−sinθr,cosθr]T,两边对时间求导,得到 n ˙ r = [ − cos θ r , − s i n θ r ] T θ r ˙ = − t r θ r ′ s ˙ = − t r κ r s ˙ \dot{\boldsymbol{n}}_r=[-\cos{\theta_r},-sin{\theta_r}]^T\dot{\theta_r}=-\boldsymbol{t_r}\theta_r'\dot{s}=-\boldsymbol{t_r}\kappa_r\dot{s} n˙r=[−cosθr,−sinθr]Tθr˙=−trθr′s˙=−trκrs˙,从而:
d ˙ = v x t x T n r − s ˙ t r T n r − [ x − r ] T t r κ r s ˙ = v x t x T n r ( t r , n r 正交 ; [ x − r ] , t r 正交) = v x [ c o s θ x , s i n θ x ] [ − s i n θ r , c o s θ r ] T = v x sin Δ θ \dot{d}=v_x\boldsymbol{t_x}^T\boldsymbol{n}_r-\dot{s}\boldsymbol{t_r}^T\boldsymbol{n}_r-[x-r]^T\boldsymbol{t_r}\kappa_r\dot{s} \\=v_x\boldsymbol{t_x}^T\boldsymbol{n}_r(\boldsymbol{t_r},\boldsymbol{n}_r正交;[x-r],\boldsymbol{t_r}正交) \\=v_x[cos{\theta_x},sin{\theta_x}][-sin{\theta_r},cos{\theta_r}]^T \\=v_x\sin{\Delta\theta} d˙=vxtxTnr−s˙trTnr−[x−r]Ttrκrs˙=vxtxTnr(tr,nr正交;[x−r],tr正交)=vx[cosθx,sinθx][−sinθr,cosθr]T=vxsinΔθ
下面推导 d ′ d' d′:
d ′ = d d d s = d d d t d t d s = d ˙ s ˙ = 1 s ˙ v x sin Δ θ d'=\frac{dd}{ds}=\frac{dd}{dt}\frac{dt}{ds}=\frac{\dot{d}}{\dot{s}}=\frac{1}{\dot{s}}v_x\sin{\Delta\theta} d′=dsdd=dtdddsdt=s˙d˙=s˙1vxsinΔθ
要把未知量 s ˙ \dot{s} s˙消掉,通过 v x v_x vx来消:
v x = ∣ ∣ x ˙ ∣ ∣ 2 = ∣ ∣ d ( r + d n r ) d t ∣ ∣ 2 = s ˙ t r + d ˙ n r − d t r κ r s ˙ = ∣ ∣ [ t r , n r ] [ 1 − κ r d 0 0 1 ] [ s ˙ d ˙ ] ∣ ∣ 2 = ( 1 − κ r d ) 2 s ˙ 2 + d ˙ 2 = ( 1 − κ r d ) 2 s ˙ 2 + d ′ 2 s ˙ 2 v_x = ||\dot{x}||_2=||\frac{d(\boldsymbol{r}+d\boldsymbol{n}_r)}{dt}||_2 \\=\dot{s}\boldsymbol{t}_r+\dot{d}\boldsymbol{n}_r-d\boldsymbol{t_r}\kappa_r\dot{s} \\=||[\boldsymbol{t_r},\boldsymbol{n_r}] \begin{bmatrix} 1-\kappa_rd & 0 \\ 0 & 1 \\ \end{bmatrix} \begin{bmatrix} \dot{s} \\ \dot{d} \\ \end{bmatrix}||_2 \\=\sqrt{(1-\kappa_rd)^2\dot{s}^2+\dot{d}^2} \\=\sqrt{(1-\kappa_rd)^2\dot{s}^2+d'^2\dot{s}^2} vx=∣∣x˙∣∣2=∣∣dtd(r+dnr)∣∣2=s˙tr+d˙nr−dtrκrs˙=∣∣[tr,nr][1−κrd001][s˙d˙]∣∣2=(1−κrd)2s˙2+d˙2=(1−κrd)2s˙2+d′2s˙2
代入可得:
d ′ 2 = ( 1 s ˙ v x sin Δ θ ) 2 = [ ( 1 − κ r d ) 2 + d ′ 2 ] sin 2 Δ θ ↓ d ′ ( 1 − sin 2 Δ θ ) = ( 1 − κ r d ) 2 sin 2 Δ θ ↓ d ′ = ( 1 − κ r d ) tan Δ θ d'^2=(\frac{1}{\dot{s}}v_x\sin{\Delta\theta})^2=[(1-\kappa_rd)^2+d'^2]\sin^2{\Delta\theta} \\\downarrow \\ d'(1-\sin^2{\Delta\theta})= (1-\kappa_rd)^2\sin^2{\Delta\theta} \\\downarrow \\ d'=(1-\kappa_rd)\tan{\Delta\theta} d′2=(s˙1vxsinΔθ)2=[(1−κrd)2+d′2]sin2Δθ↓d′(1−sin2Δθ)=(1−κrd)2sin2Δθ↓d′=(1−κrd)tanΔθ
下面推导 d ′ ′ d'' d′′,
d ′ ′ = d d d d s d s = d d ′ d s = ( − κ r ′ d − κ r d ′ ) tan Δ θ + ( 1 − κ r d ) 1 cos 2 Δ θ d Δ θ d s = − ( κ r ′ d + κ r d ′ ) tan Δ θ + ( 1 − κ r d ) 1 cos 2 Δ θ ( d θ x d s − d θ r d s ) = − ( κ r ′ d + κ r d ′ ) tan Δ θ + ( 1 − κ r d ) 1 cos 2 Δ θ ( d θ x d s x d s x d s − κ r ) = − ( κ r ′ d + κ r d ′ ) tan Δ θ + ( 1 − κ r d ) 1 cos 2 Δ θ ( d θ x d s x d s x / d t d s / d t − κ r ) = − ( κ r ′ d + κ r d ′ ) tan Δ θ + ( 1 − κ r d ) 1 cos 2 Δ θ ( κ x v x s ˙ − κ r ) d''=\frac{d\frac{dd}{ds}}{ds}=\frac{dd'}{ds}=(-\kappa_r'd-\kappa_rd')\tan{\Delta\theta}+(1-\kappa_rd)\frac{1}{\cos^2{\Delta\theta}}\frac{d\Delta\theta}{ds} \\=-(\kappa_r'd+\kappa_rd')\tan{\Delta\theta}+(1-\kappa_rd)\frac{1}{\cos^2{\Delta\theta}}(\frac{d\theta_x}{ds}-\frac{d\theta_r}{ds}) \\=-(\kappa_r'd+\kappa_rd')\tan{\Delta\theta}+(1-\kappa_rd)\frac{1}{\cos^2{\Delta\theta}}(\frac{d\theta_x}{ds_x}\frac{ds_x}{ds}-\kappa_r) \\=-(\kappa_r'd+\kappa_rd')\tan{\Delta\theta}+(1-\kappa_rd)\frac{1}{\cos^2{\Delta\theta}}(\frac{d\theta_x}{ds_x}\frac{ds_x/dt}{ds/dt}-\kappa_r) \\=-(\kappa_r'd+\kappa_rd')\tan{\Delta\theta}+(1-\kappa_rd)\frac{1}{\cos^2{\Delta\theta}}(\kappa_x\frac{v_x}{\dot{s}}-\kappa_r) d′′=dsddsdd=dsdd′=(−κr′d−κrd′)tanΔθ+(1−κrd)cos2Δθ1dsdΔθ=−(κr′d+κrd′)tanΔθ+(1−κrd)cos2Δθ1(dsdθx−dsdθr)=−(κr′d+κrd′)tanΔθ+(1−κrd)cos2Δθ1(dsxdθxdsdsx−κr)=−(κr′d+κrd′)tanΔθ+(1−κrd)cos2Δθ1(dsxdθxds/dtdsx/dt−κr)=−(κr′d+κrd′)tanΔθ+(1−κrd)cos2Δθ1(κxs˙vx−κr)
需要把未知量 s ˙ \dot{s} s˙消掉,由 0 = ( x − r ) T t r 0=(x-r)^T\boldsymbol{t}_r 0=(x−r)Ttr两边对时间求导:
0 = ( x ˙ − r ˙ ) T t r + ( x − r ) T t ˙ r 0 = v x t x T t r − s ˙ t r T t r + ( x − r ) T n r κ r s ˙ 0 = v x cos Δ θ − s ˙ ( 1 − κ r d ) ↓ v x = s ˙ 1 − κ r d cos Δ θ 0=(\dot{x}-\dot{r})^T\boldsymbol{t}_r+(x-r)^T\dot{\boldsymbol{t}}_r \\0=v_x\boldsymbol{t}_x^T\boldsymbol{t}_r-\dot{s}\boldsymbol{t}_r^T\boldsymbol{t}_r+(x-r)^T\boldsymbol{n}_r\kappa_r\dot{s} \\0=v_x\cos{\Delta\theta}-\dot{s}(1-\kappa_rd) \\\downarrow \\v_x=\dot{s}\frac{1-\kappa_rd}{\cos{\Delta\theta}} 0=(x˙−r˙)Ttr+(x−r)Tt˙r0=vxtxTtr−s˙trTtr+(x−r)Tnrκrs˙0=vxcosΔθ−s˙(1−κrd)↓vx=s˙cosΔθ1−κrd
代入,得到:
d ′ ′ = − ( κ r ′ d + κ r d ′ ) tan Δ θ + ( 1 − κ r d ) 1 cos 2 Δ θ ( κ x 1 − κ r d cos Δ θ − κ r ) d''=-(\kappa_r'd+\kappa_rd')\tan{\Delta\theta}+(1-\kappa_rd)\frac{1}{\cos^2{\Delta\theta}}(\kappa_x\frac{1-\kappa_rd}{\cos{\Delta\theta}}-\kappa_r) d′′=−(κr′d+κrd′)tanΔθ+(1−κrd)cos2Δθ1(κxcosΔθ1−κrd−κr)
由上上式也可以求得 s ˙ \dot{s} s˙:
s ˙ = v x cos Δ θ 1 − κ r d \dot{s}=v_x\frac{\cos{\Delta\theta}}{1-\kappa_rd} s˙=vx1−κrdcosΔθ
最后来求 s ¨ \ddot{s} s¨,由 a x = v ˙ x a_x=\dot{v}_x ax=v˙x:
a x = v ˙ x = s ¨ 1 − κ r d cos Δ θ + s ˙ d s d t d d s 1 − κ r d cos Δ θ = s ¨ 1 − κ r d cos Δ θ + s ˙ 2 [ ( − κ r ′ d − κ r d ′ ) 1 cos Δ θ + ( 1 − κ r d ) 1 cos 2 Δ θ sin ( Δ θ ) Δ θ ′ ] = s ¨ 1 − κ r d cos Δ θ + s ˙ 2 1 cos ( Δ θ ) [ ( − κ r ′ d − κ r d ′ ) + ( 1 − κ r d ) tan ( Δ θ ) Δ θ ′ ] a_x=\dot{v}_x=\ddot{s}\frac{1-\kappa_rd}{\cos{\Delta\theta}}+\dot{s}\frac{ds}{dt}\frac{d}{ds}\frac{1-\kappa_rd}{\cos{\Delta\theta}} \\=\ddot{s}\frac{1-\kappa_rd}{\cos{\Delta\theta}}+\dot{s}^2[(-\kappa_r'd-\kappa_rd')\frac{1}{\cos{\Delta\theta}}+(1-\kappa_rd)\frac{1}{\cos^2{\Delta\theta}}\sin(\Delta\theta)\Delta\theta'] \\=\ddot{s}\frac{1-\kappa_rd}{\cos{\Delta\theta}}+\dot{s}^2\frac{1}{\cos(\Delta\theta)}[(-\kappa_r'd-\kappa_rd')+(1-\kappa_rd)\tan(\Delta\theta)\Delta\theta'] ax=v˙x=s¨cosΔθ1−κrd+s˙dtdsdsdcosΔθ1−κrd=s¨cosΔθ1−κrd+s˙2[(−κr′d−κrd′)cosΔθ1+(1−κrd)cos2Δθ1sin(Δθ)Δθ′]=s¨cosΔθ1−κrd+s˙2cos(Δθ)1[(−κr′d−κrd′)+(1−κrd)tan(Δθ)Δθ′]
其中:
Δ θ ′ = d ( θ x − θ r ) d s = d θ x d s x d s x d s − κ r = κ x v x s ˙ − κ r = κ x 1 − κ r d c o s Δ θ − κ r \Delta\theta'=\frac{d(\theta_x-\theta_r)}{ds}=\frac{d\theta_x}{ds_x}\frac{ds_x}{ds}-\kappa_r=\kappa_x\frac{v_x}{\dot{s}}-\kappa_r=\kappa_x\frac{1-\kappa_rd}{cos\Delta\theta}-\kappa_r Δθ′=dsd(θx−θr)=dsxdθxdsdsx−κr=κxs˙vx−κr=κxcosΔθ1−κrd−κr
3 Cartesian转Frenet
-
[ X , θ x , κ x , v x , a x ] , θ r , κ r → [ s , s ˙ , s ¨ , d , d ˙ , d ¨ ] [\boldsymbol{X},\theta_x,\kappa_x,v_x,a_x],\theta_r,\kappa_r \rightarrow [s,\dot{s},\ddot{s},d,\dot{d},\ddot{d}] [X,θx,κx,vx,ax],θr,κr→[s,s˙,s¨,d,d˙,d¨]
-
s,d通过找最近点求得
-
s ˙ = v x cos ( Δ θ ) 1 − κ r d , Δ θ = θ x − θ r \dot{s}=v_x\frac{\cos(\Delta\theta)}{1-\kappa_rd},\Delta\theta=\theta_x-\theta_r s˙=vx1−κrdcos(Δθ),Δθ=θx−θr
s ¨ = cos ( Δ θ ) 1 − κ r d [ a x − s ˙ 2 cos ( Δ θ ) [ ( − κ r ′ d − κ r d ′ ) + ( 1 − κ r d ) tan ( Δ θ ) Δ θ ′ ] ] \ddot{s}=\frac{\cos(\Delta\theta)}{1-\kappa_rd}[a_x-\frac{\dot{s}^2}{\cos(\Delta\theta)}[(-\kappa_r'd-\kappa_rd')+(1-\kappa_rd)\tan(\Delta\theta)\Delta\theta']] s¨=1−κrdcos(Δθ)[ax−cos(Δθ)s˙2[(−κr′d−κrd′)+(1−κrd)tan(Δθ)Δθ′]]
κ r ′ = d 2 θ r d s 2 \kappa_r'=\frac{d^2\theta_r}{ds^2} κr′=ds2d2θr
d ′ = ( 1 − κ r d ) tan Δ θ d'=(1-\kappa_rd)\tan{\Delta\theta} d′=(1−κrd)tanΔθ
Δ θ ′ = κ x 1 − κ r d c o s Δ θ − κ r , κ x = d θ x d t 1 v x \Delta\theta'=\kappa_x\frac{1-\kappa_rd}{cos\Delta\theta}-\kappa_r,\kappa_x=\frac{d\theta_x}{dt}\frac{1}{v_x} Δθ′=κxcosΔθ1−κrd−κr,κx=dtdθxvx1
-
d ˙ = v x sin ( Δ θ ) \dot{d}=v_x\sin(\Delta\theta) d˙=vxsin(Δθ)
d ¨ = a x sin ( Δ θ ) + v x cos ( Δ θ ) s ˙ Δ θ ′ \ddot{d}=a_x\sin(\Delta\theta)+v_x\cos(\Delta\theta)\dot{s}\Delta\theta' d¨=axsin(Δθ)+vxcos(Δθ)s˙Δθ′
4 Frenet转Cartesian
-
[ s , s ˙ , s ¨ , d , d ˙ , d ¨ ] → [ X , θ x , κ x , v x , a x ] [s,\dot{s},\ddot{s},d,\dot{d},\ddot{d}] \rightarrow [\boldsymbol{X},\theta_x,\kappa_x,v_x,a_x] [s,s˙,s¨,d,d˙,d¨]→[X,θx,κx,vx,ax]
-
X = r + n r d , n r = [ − sin ( θ r ) , cos ( θ r ) ] T \boldsymbol{X}=\boldsymbol{r}+\boldsymbol{n}_rd,\boldsymbol{n}_r=[-\sin(\theta_r),\cos(\theta_r)]^T X=r+nrd,nr=[−sin(θr),cos(θr)]T
-
θ x = θ r + arctan d ′ 1 − κ r d , d ′ = d ˙ s ˙ \theta_x=\theta_r+\arctan\frac{d'}{1-\kappa_rd},d'=\frac{\dot{d}}{\dot{s}} θx=θr+arctan1−κrdd′,d′=s˙d˙
-
κ x = cos 3 Δ θ [ d ′ ′ + ( κ r ′ d + κ r d ′ ) tan ( Δ θ ) ] 1 − κ r d + κ r c o s Δ θ 1 − κ r d , d ′ ′ = d d d d s d s = d d ˙ s ˙ d s = d ¨ s ˙ − d ˙ s ¨ s ˙ 3 \kappa_x=\frac{\cos^3\Delta\theta[d''+(\kappa_r'd+\kappa_rd')\tan(\Delta\theta)]}{1-\kappa_rd}+\frac{\kappa_rcos\Delta\theta}{1-\kappa_rd},d''=\frac{d\frac{dd}{ds}}{ds}=\frac{d\frac{\dot{d}}{\dot{s}}}{ds}=\frac{\ddot{d}\dot{s}-\dot{d}\ddot{s}}{\dot{s}^3} κx=1−κrdcos3Δθ[d′′+(κr′d+κrd′)tan(Δθ)]+1−κrdκrcosΔθ,d′′=dsddsdd=dsds˙d˙=s˙3d¨s˙−d˙s¨(由 d ′ ′ d'' d′′的式子得到)
-
v x = s ˙ 1 − κ r d cos ( Δ θ ) , Δ θ = θ x − θ r v_x=\dot{s}\frac{1-\kappa_rd}{\cos(\Delta\theta)},\Delta\theta=\theta_x-\theta_r vx=s˙cos(Δθ)1−κrd,Δθ=θx−θr
-
a x = s ¨ 1 − κ r d cos Δ θ + s ˙ 2 1 cos ( Δ θ ) [ ( − κ r ′ d − κ r d ′ ) + ( 1 − κ r d ) tan ( Δ θ ) Δ θ ′ ] a_x=\ddot{s}\frac{1-\kappa_rd}{\cos{\Delta\theta}}+\dot{s}^2\frac{1}{\cos(\Delta\theta)}[(-\kappa_r'd-\kappa_rd')+(1-\kappa_rd)\tan(\Delta\theta)\Delta\theta'] ax=s¨cosΔθ1−κrd+s˙2cos(Δθ)1[(−κr′d−κrd′)+(1−κrd)tan(Δθ)Δθ′]
κ r ′ = d 2 θ r d s 2 \kappa_r'=\frac{d^2\theta_r}{ds^2} κr′=ds2d2θr
这篇关于【自动驾驶坐标系基础】Frenet坐标系和Cartesian坐标系的相互转换的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








