【题目来源】http://poj.org/problem?id=2201【题目描述】 Let us consider a special type of a binary search tree, called a cartesian tree. Recall that a binary search tree is a rooted ordered binary tree, such that

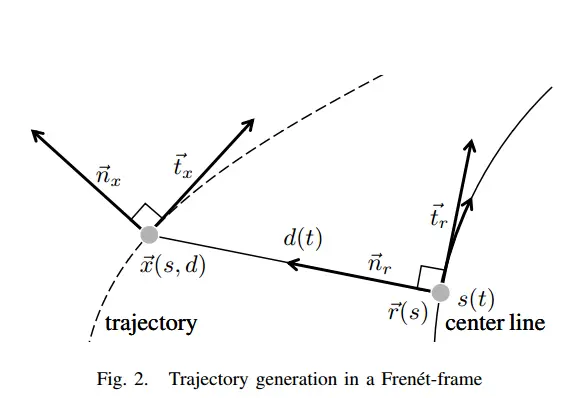
Frenet坐标系和Cartesian坐标系的相互转换 2023.12.12 1 变量含义 Frenet和Cartesian相互转换即 [ s , s ˙ , s ¨ , d , d ˙ , d ¨ ] ↔ [ X , θ x , κ x , v x , a x ] [s,\dot{s},\ddot{s},d,\dot{d},\ddot{d}] \leftrightarrow[\bol

已知是heaporder对inorder排序，然后gen树，要判断在inorder前一个节点的左右，就可以左右依次gen，得到相应的内容； 也可以不用gen树拿到最小值和index直接保存层序遍历，最小堆，最小值就是根节点划开左右branch，使用map自动排序的特点 不能使用数组存储res(10741824, -999) res[index] = v[pot]; 会越界，要使用map存储

本文主要使用并行成像和压缩感知方法实现non-Cartesian MRI 数据的重建。 目录 1 自定义MRI kspace trajectory 2 自定义该 trajectory下的多通道MRI数据 3 使用NUFFT 直接做欠采样数据的重建

前文中我们已经了解了一些用于循环的关键字，比如 with_list、with_items、with_flattened、with_together，这篇文章我们继续。 假设，现在我有一个需求，我需要在目标主机的测试目录中创建a、b、c三个目录，这三个目录都有相同的子目录，它们都有test1和test2两个子目录，使用最原始的办法，我们可以在目标主机上执行如下一堆命令 # pwd/testdi

JavaPairRDD的cartesian方法讲解 官方文档说明 Return the Cartesian product of this RDD and another one, that is, the RDD of all pairs of elements (a, b) where a is in `this` and b is in `other`. 中文含义 该函数返回的是P

Let X, X′ , Y, Y ′ be sets. Let × denote the Cartesian product of sets. Show that X × Y − X ′ × Y ′ = ((X ∩ X ′ ) × (Y − Y ′ )) ∪ ((X − X ′ ) × Y ) . Solution:(x, y) ∈ LHS ⇔x ∈ X ∧ y ∈ Y ∧ ¬(x ∈ X′∧

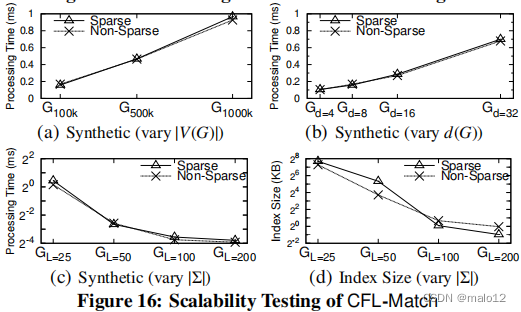
Bi F, Chang L, Lin X, et al. Efficient subgraph matching by postponing cartesian products[C]//Proceedings of the 2016 International Conference on Management of Data. 2016: 1199-1214. 文章目录 ABSTRACT1

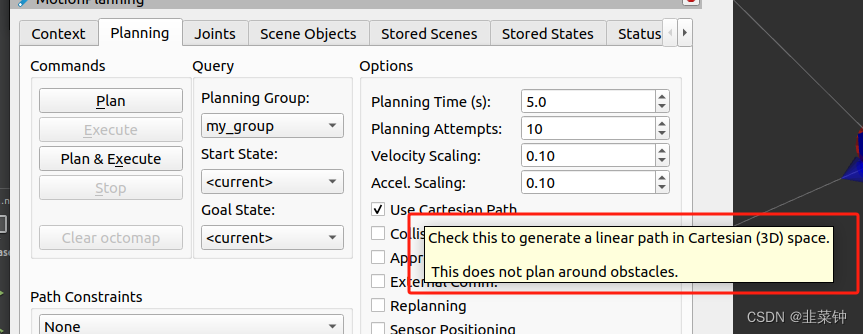
文章目录 rviz中的【Use Cartesian Path】C++接口中的【computeCartesianPath】！！！特别注意！！！ rviz中的【Use Cartesian Path】 在rviz中使用MoveIt时，在MotionPlanning选项卡有一个【Use Cartesian Path】的选项，勾选之后，规划出来的路径是两个移动点的直线路径。 上图中的显示轨