【论文阅读】Efficient Subgraph Matching by Postponing Cartesian Products

Bi F, Chang L, Lin X, et al. Efficient subgraph matching by postponing cartesian products[C]//Proceedings of the 2016 International Conference on Management of Data. 2016: 1199-1214.

文章目录

• ABSTRACT
• 1. INTRODUCTION
• 2. PRELIMINARIES
• • 2.1 Existing Subgraph Matching Algorithms
• 3. A NEW FRAMEWORK
• 4. OUR APPROACHES
• • 4.1 Auxiliary Data Structure
  • 4.2 CPI-based Core-Match
  • • 4.2.1 CPI-based Matching Order Selection
    • 4.2.2 CPI-based Embedding Enumeration
  • 4.3 CPI-based Forest-Match
  • 4.4 CPI-based Leaf-Match
• 5. CPI CONSTRUCTION
• • 5.1 General Idea
  • 5.2 Top-Down Construction
  • 5.3 Bottom-Up Refinement
  • 5.4 Analysis of CPI Construction
• 6. EXPERIMENTS
• • 6.1 Comparing with Existing Techniques
  • • Eval-I: Against Existing Algorithms by Varying |V(q)|
    • Eval-II: Evaluating Enumeration Time for Core-Structures of Queries
    • Eval-III: Varying #Embeddings
    • Eval-IV: Evaluating The Boost Technique in [14]
  • 6.2 Effectiveness of New Framework
  • • Eval-V: Evaluating Our Framework
    • Eval-VI: Evaluating the Effectiveness of CPI Construction Strategies
    • Eval-VII: Scalability Testing
• 7. CONCLUSION

ABSTRACT

摘要研究了提取大数据图g中查询图q的所有子图同构嵌入的子图匹配问题。现有的子图匹配算法采用Ullmann的回溯方法，即按照查询顶点的匹配顺序，将查询顶点迭代映射到数据顶点。结果表明，查询顶点的匹配顺序是提高子图匹配算法效率的一个重要方面。近年来，许多先进的技术，如加强连接和合并查询或数据图中的相似顶点，被提出，以提供有效的匹配顺序，以减少希望的中间结果，特别是由冗余笛卡尔积引起的结果。在本文中，我们首次解决了来自“不同”顶点的笛卡尔乘积的结果不佳的问题。我们提出了一种新的框架，通过基于查询结构的延迟笛卡尔积来最小化冗余的笛卡尔积。我们的第二个贡献是提出了一种新的基于路径的辅助数据结构，大小为O（|E (G)|的|×|V (q)|）来生成匹配顺序并进行子图匹配，这大大减少了现有基于路径的辅助数据结构的指数大小O（|V(G)|）的|V(q)|−1)，其中V (G)和E (G)分别是数据图G的顶点和边集，V (q)是查询q的顶点集。对真实图和合成图的广泛实证研究表明，我们的技术比最先进的算法多出3个数量级。

1. INTRODUCTION

近年来，图分析在数据分析领域发挥着越来越重要的作用。子图匹配是图分析中最基本的问题之一。给定一个查询图q和一个大数据图G，子图匹配的问题是提取所有子图同构嵌入q。子图匹配有广泛的应用，包括蛋白质相互作用网络分析[13]、社会网络分析[17]和化合物搜索[20]。尽管子图匹配[5]具有np完备性，但最近的研究工作在开发组合方面取得了重大进展进行子图匹配[4,8,14,15,22]的范例。
一个关键问题是，当迭代地将顶点一个接一个地从查询图映射到数据图时，减少无希望的中间结果的数量，特别是防止产生冗余笛卡尔积造成的无希望的直接结果。VF2 [4]和QuickSI [15]提出强制连通性以减少冗余笛卡尔积；也就是说，防止在两个不相交的子图q1和q2中生成中间嵌入，这样q1中没有一个顶点和q2中没有另一个顶点。进一步减少不必要的枚举笛卡尔产品的机会，TurboISO [8]提出合并相似的顶点查询图q（例如，顶点与相同的标签和相同的社区），和[14]显著扩展[8]的工作压缩数据图G通过合并一起相似的顶点G提高[8]技术的性能。
第二个关键问题是为从查询图到数据图的逐个迭代映射顶点生成一个有效的匹配顺序，目的是最小化中间结果的总数。QuickSI [15]提出基于不常见标签第一策略生成匹配顺序。SPath [22]提出基于不常路径优先策略生成匹配顺序，以解决[15]中只考虑顶点和边的局限性。[8]中的TurboISO技术提出了精确地枚举所有路径，以克服[22]中可能通过估计公式高估连接基数的限制。
挑战和我们的方法。我们最初的实证研究表明，当查询图的大小变大时，TurboISO [8]及其boost [14]的效率可能非常低。这促使我们开发新的、更有效的和可伸缩的技术来进行子图匹配。以下是我们将在本文中处理的两个挑战。

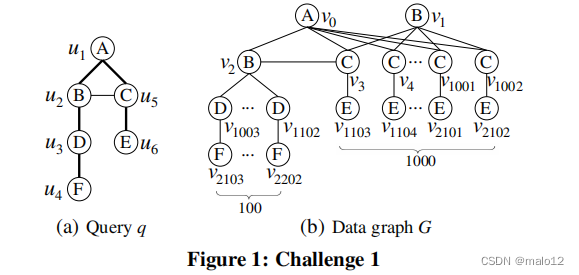
挑战1：由不同顶点的冗余笛卡尔积。考虑图1(a)中的查询q和图1(b).中的数据图Gq和G不能分别被[8]和[14]中的技术直接压缩，因为没有相似的q或G中的顶点（即，没有具有相同标签和相同邻域的顶点）。请注意，最近的技术[8,14,15,22]都是基于沿着q的生成树迭代地从q（即嵌入）映射到G，并检查q中新扩展顶点附近的非树边。假设q的生成树qT如图1(a)中的粗线所示，即（u1、u2）、（u2、u3）、（u3、u4）、（u1、u5）和（u5、u6）。最先进的基于边缘的排序（即QuickSI）和基于路径的排序（即TurboISO）技术都将选择qT中的匹配顺序为（u1、u2、u3、u4、u5、u6）。因此，在检查非树边缘（u2、u5）的映射之前，100部分映射（v0、v2、v1000+i，v2100+i）（3≤i≤102）（u1、u2、u3、u4）的1000部分映射（v0、vj）（3≤j≤1002）相结合。显然，在这种情况下，（100000−100）部分映射的笛卡尔积是假阳性和冗余的。

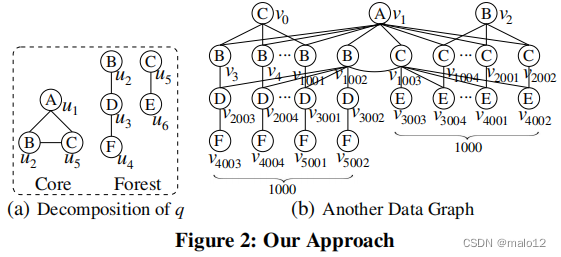
我们的方法是：推迟笛卡尔式的乘积。对于上面的例子，如果我们使用匹配的顺序（u1u2u5u3u4u6），那么我们可以避免这个100×1000局部映射的笛卡尔积。事实上，第二个匹配顺序只导致100 + 1000个局部映射，因为早期检查非树边（u2，u5）可以消除（u1，u5）的999个局部映射（v0，vj）（4≤j≤1002）。通过将一个查询图分解为一个密集的子图（即核心）和一个森林，我们可以将其推广为一个新的框架；例如，图2(a)说明了图1(a).中查询图的这种分解请注意，密集的查询子图具有更强的剪枝能力（因此，减少了没有希望的部分映射的数量），而森林在g中可能有更多的映射。因此，首先处理核心可能会推迟笛卡尔积，从而减少生成冗余笛卡尔积的机会。
此外，我们还可以通过处理最后一个查询的所有叶（即1次）顶点（如果存在），从而进一步推迟可能的冗余笛卡尔积。例如，假设现在的数据图是图2(b)中的那个，我们处理最后一个图中q的叶顶点u4和u6。在这种情况下，将生成由（u1、u2、u5、u3）诱导的q子图的1000个部分映射。然而，我们将把它们的笛卡尔积与（u5，u6）的1000个映射留到最后一个。这样做的好处是，如果图1(a)中的查询图有额外的部分，那么这种笛卡尔积可能是冗余的；因此应该推迟，以避免。
挑战2：TurboISO中基于路径的数据结构的指数大小。最先进的方法，TurboISO [8]，优于其他方法由于其精确计算连接基数的根叶查询路径查询q和所有嵌入的具体化数据图的查询路径，这样他们可以用来生成子图同构嵌入。这立即导致指数大小的O（|V(G)||V(q)|−1）的路径嵌入在最坏的情况下，在|V (G)|和|V (q)|顶点的数量在数据图G和查询图q，分别（见4.1节更多细节）。为了解决这个问题，TurboISO [8]仅在其实现中使用如果我们只检索q个查询路径的k个子图同构嵌入，则确定k个嵌入，以计算查询顶点的匹配顺序。注意，这样的物化并不能总是保证为q生成k个子图的同构嵌入。因此，在枚举子图同构嵌入时，可以根据需要实现更多的路径嵌入。此外，如果我们想要检索所有的子图同构嵌入，那么我们必须实现所有的路径嵌入；也就是说，在最坏情况下，TurboISO中指数大小是不可避免的。因此，TurboISO不能扩展到大型查询或大型数据图。
我们的方法：基于多项式大小的紧凑路径的数据结构。如[8]所示，基于路径的辅助数据结构可以大大加快子图匹配的计算速度。为了解决TurboISO中基于路径的数据结构的指数大小问题，在本文中，我们建议不枚举和物质化查询路径的所有嵌入。相反，我们计算一个数据结构，称为紧凑路径索引（CPI），以存储每个查询路径的嵌入的候选对象。由于我们从CPI中生成子图同构嵌入，因此CPI的规模越小，进行子图匹配的效率就越高。我们可以表明，虽然最小化CPI的大小是np困难，我们的技术生成的CPI的大小是多项式O（|E (G)|×|V (q)|）和我们的CPI构建算法运行在O（|E (G)|×|E (q)|）时间，其中|E (G)|和|E (q)|分别是G和q的边数。
此外，本文还提出了基于代价模型和CPI来计算查询顶点的匹配顺序。我们的实验表明，我们的排序技术明显优于现有的技术。
贡献。我们的主要贡献总结如下。•我们开发了一个新的框架，旨在推迟笛卡尔人的产品。新的框架将一个查询图分解为一个核心和一个森林，用于子图匹配，并建议处理最后一个查询（如果存在的话）的所有叶顶点。我们还开发了一种有效的技术来压缩叶顶点的映射，以避免产生冗余的笛卡尔积。
我们设计了一个紧凑的基于辅助路径的数据结构CPI，大小为O（|E(G)|×|V(q)|），用于准确估计查询路径的嵌入数量，并生成子图同构嵌入。
在证明最小化CPI是np困难的同时，我们提出了一种有效的启发式方法来在O（|E (G)|×|E (q)|）时间内构建CPI。
我们开发了高效的子图匹配算法。
我们在各种数据集和查询设置上进行的广泛实验表明，我们的技术比最先进的技术[8,14]高出3个数量级，甚至排除了TurboISO [8]及其boost [14]不能终止的情况。
组织本文的其余部分组织如下。下面是对相关工作的简要概述。第2节的解定义了子图匹配的问题。第3节介绍了我们推迟笛卡尔产品的新框架。我们在第4节中提出了基于CPI的技术，而在第5节中提出了CPI构建技术。实验结果见第6节。我们在第7节中给出了一个结论。由于空间限制，证据被省略，可在附录的A.1节中找到。
相关工程。相关作品的分类如下。
1)在单个大数据图上的子图匹配。在单个大图上的子图匹配问题已经被研究了几十年。第一个结果是乌尔曼在1976年提出的算法[19]，它通过根据查询顶点的输入顺序，迭代地将顶点从查询图q逐个映射到数据图G。为了提高性能，VF2 [4]和QuickSI [15]中使用了连接匹配顺序，建议通过选择一个连接到已经选择的顶点的顶点而不是随机选择来生成匹配顺序；这可以在早期阶段修剪假阳性候选，特别是那些由冗余笛卡尔积引起的。QuickSI [15]提出通过首先处理G中不常见的q的顶点和边来进一步去除假阳性候选点。GraphQL [9]和SPath [22]专注于利用基于邻域的过滤来减少查询顶点的候选点。如前所述，TurboISO [8]和[14]中的boost技术提出分别合并q和G中相似的顶点（即具有相同标签和相同邻域的顶点）。在本文中，我们提出了一种新的有效的子图匹配技术。首先，我们首次解决了来自“不同”顶点的笛卡尔积，以及来自相似顶点[8,14]的笛卡尔积的不希望结果的问题。其次，我们提出基于代价模型和[15]中基于路径的数据结构计算一个连接的查询顶点的匹配顺序，而不是简单的边缘频率。第三，我们提出了一种新的轻量级候选过滤技术，除了现有的[9,22]顶点之外，还要减少查询的候选顶点。
虽然上面的技术是基于深度优先的范式，显示为最有效的策略进行子图匹配在一台计算机上，子图匹配的问题也被调查在一个分布式环境[11,16,18]，加入范式已被证明是最受欢迎的策略。本文的目标是在一台计算机上开发新的技术，以解决现有技术中的可扩展性问题。最近，在数据库社区（如[21,24]）中也研究了相似度子图匹配的问题，即从一个与查询图相似的大数据图中检索所有的子图。本文的贡献也可能有助于研究相似度子图的匹配问题。
2)在图数据库上的子图约束搜索。在图数据库上进行子图包含搜索的问题是识别包含查询图的数据图（来自图数据库）。这涉及到在图数据库上执行子图的同构搜索。为了有效地进行这一点，已经提出了许多基于图特征的方法，遵循过滤和验证框架，可以分为两类：基于频繁子图挖掘的方法（例如，gIndex [20]、Tree+∆[23]和FG-Index [3]）和基于穷举枚举的方法（例如，gCode [25]、CT-Index [10] GraphGrepSX [2]和Grapes [7]）。虽然子图包含搜索和子图匹配都涉及子图同构搜索，但它们本质上是不同的；本文所研究的子图匹配问题比较困难，因为它需要列举所有的嵌入。

2. PRELIMINARIES

在本文中，我们重点关注一个顶点标记的无向图g =（V，E，l，Σ）。这里，V是顶点的集合，E⊆V×V是边的集合，Σ是标签的集合，l是一个标记函数，它在Σ中分配每个顶点V∈V一个标签（记为lg (v)）。g中的顶点数和边数分别用|V (g)|和|E (g)|表示。g中v∈V (g)的邻居集合用Ng (v) = {v 0∈V (g) |（v，v 0）∈E (g)}表示，v的度，记为dg (v)，为v（即dg (v) = |Ng (v)|）的邻居数。给定V的一个子集Vs，g的子图被诱导为Vs是g[Vs] =（Vs，{（u，v）∈E | u，v∈Vs}，l，Σ）。下面，为了便于表示，我们简单地将一个顶点标记的无向图称为图。请注意，我们的技术可以很容易地扩展到处理边标记图和有向图。
定义2.1：给定图q = (V (q)、E (q)、l、Σ）和G =（V (G)、E (G)、l、Σ），q是子图与G同构，当且仅当存在从V (q)到∀(∈V(q)（∀），使得∀（M(u)）和∀(∈E(u)(M(u)，M（M（u0））∈E (G)，其中M (u)是u映射到的顶点。

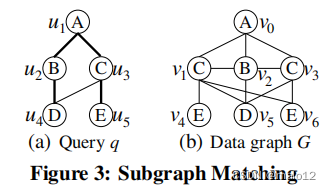
我们称一个内射映射从顶点q顶点在G子图同构嵌入q。例如，考虑图q图3(a)和图3(b){，B，C，D，E}是顶点标签，q是子图同构G因为有一个子图同构嵌入M（u1→v0，u2→v2，u3→v3，u4→v5，u5→v6）。
问题声明。给定一个查询q和一个大数据图G，在本文研究子图匹配的子图同构嵌入问题的图3(a)的数据图G的映射（u1、u2、u3、u4、u5）映射到（v0、v2、v1、v5、v4）、（v0、v2、v1、v5、v6）和（v0、v2、v3、v5、v6）。
在本文的其余部分中，为了简化没有歧义时，我们使用术语“嵌入”来表示“子图同构嵌入”，并且我们可以互换地使用嵌入和映射。当上下文清楚时，我们还将lg (v)、Ng (v)和dg (v)分别简化为l (v)、N (v)和d (v)。我们假设查询图q和数据图G都是连通的。

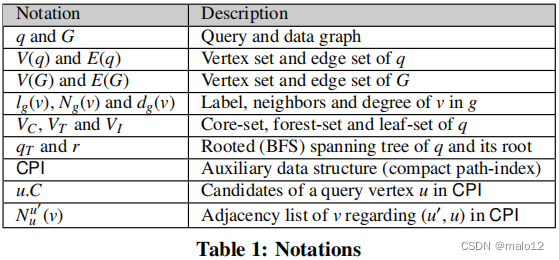
表1总结了经常使用的符号。

2.1 Existing Subgraph Matching Algorithms

子图匹配的研究由乌尔曼的回溯算法[19]发起，该算法根据查询顶点的输入顺序，迭代地将顶点从查询图q一个接一个地映射到数据图G。为了提高性能，[4,8,14,15]中后来的算法都强制执行了匹配序列/顺序的连通性。也就是说，给定q的生成树qT，构造qT的匹配顺序（u1，…，un），对于除了u1之外的每个顶点ui，它的父ui。qT中的p总是以匹配的顺序在ui之前。这被称为连接匹配顺序。例如，假设图3(a)中查询图的生成树由边（u1、u2）、（u2、u4）、（u1、u3）和（u3、u5）组成，那么可能的连接匹配顺序为（u1、u2、u3、u4、u5），其中u4.p = u2。
子图匹配算法通过根据匹配顺序将q的每个查询顶点ui映射到g中的一个数据顶点来增长嵌入M。当映射ui时，算法迭代尝试与ui的映射M（ui .p）相邻的每个数据顶点v作为ui的候选映射；v是ui的成功映射，2)它满足查询中非树边指定的所有连接要求(即，对于每个（uj，ui（<）∈E(q)（M（u<），v）∈E (G)）。如果每个查询顶点都被映射到一个数据顶点，则可以获得一个完整的嵌入。例如，考虑上述对q和图3(b).中的数据图G的匹配顺序假设部分嵌入M映射u1、u2、u3和u4分别映射到v0、v2、v1和v5。然后，对于映射u5，算法迭代尝试与M（u5.p）（= M（u3）= v1）相邻的v4和v6，以扩展M。
子图匹配算法的代价模型。在本文中，我们采用[15]中的代价模型来计算匹配顺序；即，子图匹配的回溯算法的总代价为Tiso=B1+Pni=2PBi−1j=1dij（ri+1）。这里，Bi（称为搜索宽度）是由{u1诱导的q的子图的嵌入总数，…dij是Mi j−1（ui.p）的邻居的数量，在G中有相同的标签，其中Mi j−1是由{u1诱导的子图的嵌入。，ui−1}和Mi j−1（ui.p）是qT映射中ui的父ui的顶点，ri是ui和ui之前顶点之间的非树边数。直观地说，G中部分嵌入Mi j−1（u1，…）的uij−1通过将ui映射到G中与Mi j−1（ui.p）相邻，并且与ui具有相同的标签（有di j这样的顶点）；如果v满足ui的ri非树边指定的所有连接要求，则是ui的成功映射。示例2.1：给定图3(a)、r3 = 0和u4=1中q的匹配顺序（u1、u2、u3、u4、u5）。M2 1 = {u1→v0，u2→v2}，然后M2 1（u3.p）（= v0）的邻域是v1和v3，因此是d 1 3 = 2。

3. A NEW FRAMEWORK

在本文中，我们提出了一个新的子图匹配框架，旨在延迟笛卡尔积。我们首先将一个查询图分解为三个子结构，然后以子结构对子结构的方式进行子图匹配。在下面，我们首先定义了核心-森林-叶子的分解。
Core-Forest-Leaf（CFL）分解。核心林叶分解包括核心森林分解和森林叶分解。
核心森林分解。对于q的生成树qT，q的边可以分为两类：qT中的边称为树边，而q的不属于qT的边对于qT的边称为非树边。我们的核心森林分解是计算一个小的密集的子图，其中包含关于任何生成树的所有非树边，其定义如下。
定义3.1：给定一个查询q，q的核心森林分解是计算q的最小连通子图g，该图包含q的任何生成树的所有非树边；g称为q的核心结构。q的子图组成的所有其他边不是共同重组被称为森林结构q，表示t.我们在引理3.1证明q的核心结构的q，2核q的最大子图，这样每个顶点的子图至少有两个邻居的子图。注意，q的2核是q的顶点诱导子图，它是连通的、唯一的[1]。
引理3.1：q的核心结构是q的2核结构。

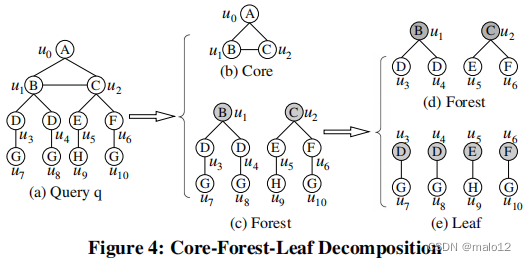
我们将核心结构的顶点集称为核心集，并将其表示为VC；然后，核心结构是q[VC]。核心森林分解的一个最重要的特征是，核心结构是包含关于q的任何生成树的q的所有非树边的最小连通子图。如引言中的挑战1所示，q的良好匹配顺序需要尽早进行所有非树边检查，这不仅可以修剪希望的部分映射，还可以减少非树边检查的总数。因此，我们将VC的所有顶点放在匹配顺序的开头。请注意，核心结构是一个连通的子图，它需要生成一个连通的匹配顺序；这对于有效的子图匹配[4,15]是至关重要的。
计算核心森林的分解。根据引理3.1，我们通过迭代去除q中的所有的1次顶点来计算核心集VC，最后一个剩余的顶点集是VC。这个迭代删除1次顶点的过程可以在关于查询大小的线性时间内实现（即，在O（|E (q)|）时间内）[1]。例如，图4(b)和4©显示了图4(a).中查询的核心-森林分解的结果最初，{u7、u8、u9、u10}是1度顶点的集合，删除它会创建新的1度顶点{u3、u4、u5、u6}，然后这些顶点也会被删除。最后，核心集为VC = {u0，u1，u2}，如图4(b).所示注意，如果q本身是一个树，那么核心集只是q的根顶点，其选择将在附录中的A.6节中讨论；整个查询q可能是核心结构。
需要注意的一件事是，森林结构由一组连接的树组成，而森林结构T中的每一棵连接的树与核心结构恰好共享一个顶点。共享顶点作为树和协同重组之间的连接顶点。例如，u1和u2分别由图4©中的核心结构和两个连接的树共享。
林叶分解。如引言中的挑战1所示，一个良好的匹配顺序还需要推迟由所有叶顶点的候选项引起的笛卡尔积。因此，我们进一步将通过核心森林分解得到的森林结构T分解为森林集VT和叶集VI，并将VI的所有顶点放到匹配顺序的末尾。
定义3.2：给定森林结构T，森林-叶分解是通过在T的每棵树的连接顶点上生根来计算T的叶顶点的集合VI。q不在VC∪VI中的其他顶点的集合称为q的森林集，记为VT。
因此，V (q) = VC∪VT∪VI和VC∩VT=VC∩VI=VT∩VI=∅。例如，图4(d)和图4(e)是图4©.中森林结构T的森林-叶片分解的结果在下面，我们简单地在从T中去除VI的所有顶点及其关联的边后，将T的子图称为森林结构。
基于CFL-分解的框架。从上面对一个查询q的核心-森林-叶分解中，我们得到了三个顶点集，即核心集VC、森林集VT和叶集VI。我们将q的查询顶点的宏排序定义为（VC、VT、VI）；我们首先将VC的顶点，然后是VT的顶点，最后是VI的顶点，映射到数据顶点。因此，我们提出了一个新的高效、可伸缩的子图匹配框架，其伪代码见算法1，表示为CFL-Match。

给定一个查询q，我们首先计算它的核心-森林-叶分解（VC，VT，VI）（Line 1），这已经在上面讨论过了。然后，我们建立了一个辅助的数据结构，称为紧凑路径指数（CPI），用于关于数据图G（第2行）的查询q；CPI构造的细节将在第5节中讨论。最后，基于构建的CPI，我们分别进行了核心匹配（第4行）、森林匹配（第5行）和叶匹配（第6行）；这些匹配算法的细节将在第4节中讨论。请注意，每次当我们调用核心匹配或森林匹配或叶匹配时，它都会返回下一个嵌入；也就是说，为了节省内存空间，每次只生成一个嵌入。
基于CFL-分解的框架的好处。考虑图1(a)中的查询q和引言中的图1(b)中的数据图G。对于与u5匹配的顺序（u1、u2、u3、u4、u4、u5、u6），搜索呼吸（见第2.1节）为B1 = 1、B2 = 1、B3 = 100、B4 = 100和B5 = 100。由于只有u5具有非树边，关于此匹配顺序的子图匹配的总成本（见第2.1节）是Tiso=B1+B1×1×1×1+B2×100×1+B3×1×1 + B4×1000×2 + B5×1×1 = 200302。我们基于核心-森林-叶分解的框架将生成匹配的顺序（u1、u2、u5、u5、u3、u4、u6），在早期阶段进行非树的边缘检查，然后成本变成T 0iso = 2302，明显小于Tiso。此外，通过我们的新框架，可以立即将由叶查询顶点引起的笛卡尔积放到子图匹配过程的末端。

4. OUR APPROACHES

在本节中，我们提出了一种新的辅助数据结构，称为紧凑路径索引（CPI），用于有效地进行子图匹配。接下来，我们首先在第4.1节中定义紧凑路径索引（CPI），然后在第4.2、4.3和4.4节中分别给出我们基于CPI的核心匹配、森林匹配和叶匹配，而CPI构建算法将在第5节中介绍。

4.1 Auxiliary Data Structure

为了紧凑地编码查询的所有可能嵌入到数据图中，我们提出了一种新的辅助数据结构，称为紧凑路径索引（CPI）。CPI不仅删除查询顶点的假阳性候选，还用于计算有效匹配顺序（参见第4.2节）。
CPI结构。给定一个查询q和一个数据图G，CPI被定义为一个q的BFS树qT，并具有与qT相同的结构。为了区分CPI的顶点和q和G的顶点，我们称CPI的顶点为节点。CPI中的每个节点u都具有与qT中相同的标签（即lq (u)）。与qT中的父子关系类似，CPI中的任何两个相邻节点也有父子关系。
CPI的结构如下。
CPI的每个节点u都有一个候选集，记为u。C，它存储了你可以映射到的G的所有顶点。
在v∈u之间有一条边。C和v0∈u0。因此，构造CPI等价于计算一个候选集u。C表示q的每个查询顶点u。

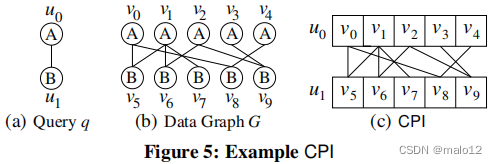
例如，图5©显示了为图5(a)中的查询q在图5(b).中的数据图G上构造的CPIu0和u1的候选集是u0。C={v0，…，v4}和u1。C={v5，…分别，v9}。u0.C中的顶点与u1.C中的顶点之间的边与数据图中的边完全相同，如图5©.中的CPI所示需要注意的一件事是，G的一个数据顶点可能会出现在CPI中多个节点的候选集合中。我们的CPI存储表示将在附录中的A.2节中讨论。
坚固性。我们的目标是直接使用CPI，构造查询q数据图G，计算所有的嵌入qG.数据图G只探测非树边缘检查（即检查，检查是否存在一个边缘之间的两个映射的端点非树的边缘）。为了实现这一点，CPI必须满足以下可靠性要求：
对于CPI中的每个节点u，如果在G中有一个嵌入的q，将u映射到v，那么v必须在u中。C.
如果一个CPI满足稳健性要求，那么它就是健全的。请注意，尽管在稳健性要求中，我们只考虑查询顶点的候选边，但根据我们的CPI识别，父子查询顶点之间的候选边会自动包括在内。关于一个健全的CPI，我们有以下定理。
定理4.1：给定一个健全的CPI，G中q的所有嵌入都可以通过遍历CPI来计算，而G只用于非树边检查。
一个健全的CPI的大小。一个简单强壮的CPI可以通过让u。C为G所有标记lq的顶点的集合(u)。朴素的CPI将包含大量的查询顶点的假阳性候选项，这将极大地影响子图匹配算法的运行时间，因为它生成的许多部分嵌入最终会被修剪。一个自然的目标是构建一个最小且健全的CPI；也就是说，CPI中的候选查询顶点集的总大小是最小的。然而，这是np困难的，如下面的引理所示。
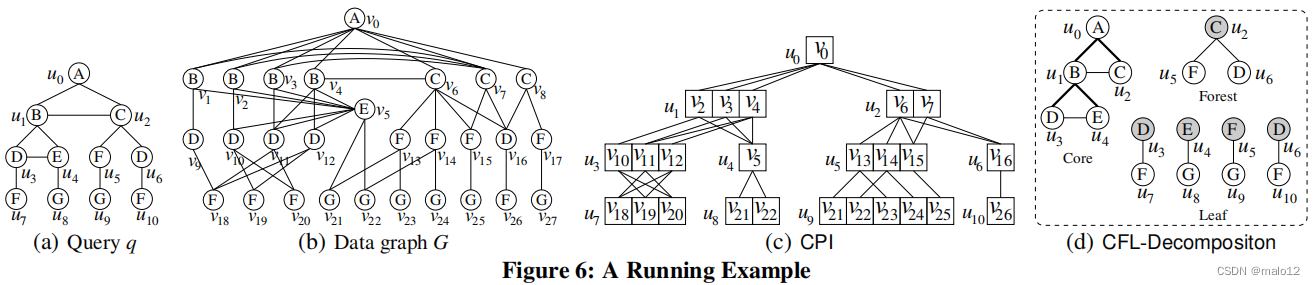
引理4.1：建立一个最小且健全的CPI很难得到NP值。然而，为数据图G查询q构建的CPI的最坏情况大小是O（|V（|）|×|E (G)|），尽管在G中可以有指数数量的嵌入。这是因为，i)查询顶点的候选集的大小最多是|V (G)|，2)对于CPI中的父子节点（u，u0），所有邻接列表Nuu0（·）的大小最多是|E (G)|，因为没有重复的边，并且iii)有|V (q)|查询顶点和（|V (q)|−1）副子节点对。此外，对于带有|Σ|个不同标签的数据图G，CPI的平均最坏情况大小为O（|V(q)|×|E(G)||Σ|2+|V(q)|×|V(G)||Σ|）。这是因为一个查询顶点的候选集的平均大小是|V (G)|/|Σ|，而与一对父子查询顶点对应的所有邻接列表的平均总大小是|E (G)|/|Σ| 2，在CPI中，G的一条边出现在CPI的邻接列表中的概率为1/|Σ| 2。在本文中，我们的目标是建立一个小型而健全的CPI，这将在第5节中详细讨论。例如，图6©显示了由我们的算法为图6(a)中的查询在图6(b).中的数据图上构建的CPI。

备注。TurboISO [8]还提出了一种辅助数据结构，将查询生成树的所有根到叶路径存储到数据图中。然而，CPI在本质上是不同的。一个主要的区别是，TurboISO中的数据结构可以是指数级大小的（即，空间复杂度为O（|V(G)||V(q)|−1）），因此构造时间也是指数级的。为了解决这个问题，TurboISO [8]只为每个从根到叶的查询路径实现了k个嵌入，其中k是在计算查询顶点的匹配顺序时，要报告的子图同构嵌入的数量；在枚举子图同构嵌入时，可以根据需要实现更多的路径嵌入。但是，如果我们想检索所有的子图同构嵌入，我们仍然必须实现所有的路径嵌入；也就是说，在最坏的情况下，在TurboISO中，指数大小是不可避免的。因此，TurboISO不能扩展到大型查询或大型数据图。有关这些问题的详细讨论，请参见附录中的A.3节。

4.2 CPI-based Core-Match

给定数据图G上的查询q有一个良好的CPI，G中q的所有嵌入都可以通过遍历CPI来计算，而G只用于非树的边缘检查。在这里，为了简单地表示，我们假设q本身是核心结构；否则，我们只考虑CPI中对应于q的核心结构的部分。下面，我们首先给出了基于cpi的匹配顺序选择，然后描述了嵌入枚举方法。

4.2.1 CPI-based Matching Order Selection

我们计算查询顶点的匹配顺序的算法是一个基于路径的排序。回想一下，CPI对应于q的BFS树，从中我们可以得到一组根到叶路径{π1，……，πk}，所有k条路径共享CPI的根节点。我们的目标是计算k个路径的有效排序。
查询顶点的匹配顺序序列可以通过路径的顺序得到。假设路径的排序为（π1，……，πk）。我们将seq初始化为π1，然后迭代地添加πi的顶点到i = 2的seq中，……，k。当将πi =（vi1，……，viy）的顶点添加到seq时，很容易看到πi与seq共享一个前缀；我们将最后一个共享顶点vix称为πi的连接顶点，并表示为πi .p，类似于第2.1节中讨论的u.p。然后，我们添加顶点vix+1，……，从πi到seq。例如，对于图6©中的CPI，核心结构的BFS树由三条路径π1 =（u0、u1、u3）、π2 =（u0、u1、u4）和π3 =（u0、u2）组成。假设路径的顺序为（π2、π1、π3），则查询顶点的匹配顺序为（u0、u1、u4、u3、u2）。
基于基于路径排序的子图匹配的成本分析。
从第2.1节中回想一下，一个子图匹配的总成本基于匹配顺序（u1，……，un）的算法是Tiso=B1+Pni=2PBi−1j=1dij（ri+1）[15]。对于基于路径的排序（π1，…，πk），假设匹配顺序为（u1，…，un），πi的叶（即最后一个顶点按匹配顺序）的位置为li。然后，将匹配成本改写为，

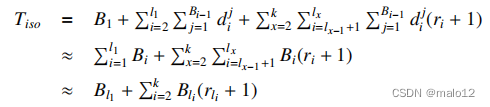
第一个方程遵循没有非树边缘在BFS树的路径，和接下来的两个方程遵循两个假设：1)PBi−1j=1dij≈毕，和2)Plxi=lx−1+1Bi（ri+1）≈Blx（rlx + 1）。注意，在CPI的帮助下，给定查询顶点（u1，…，ui−1）的部分映射（v1，…，vi−1），将部分映射通过考虑CPI中的每个顶点v∈Nu u i j（vj）作为ui的候选来扩展，其中uj是CPI中ui的父对象。第一个假设是，在CPI中嵌入(u1，……基于N u ui j（vj）的每个扩展将导致嵌入（u1，……，ui）；这是基于在构建CPI时已经利用了非树边的修剪（见第5节）。第二个假设自然遵循基于路径的排序策略；也就是说，我们假设映射查询路径的顶点的最大代价决定了映射路径的代价。
对排序路径的一种贪婪的方法。请注意，在匹配的顺序中，ui和ui之前的顶点之间的非树边数（即ri）取决于实际的匹配顺序。由于配置ofris的总数为指数级（即O（|V (q)|！）)，考虑ri来优化Tiso将太昂贵。因此，我们代替而最小化Tiso，˜Tiso=Pki=1Bli的近似值（即，qT的叶顶点的搜索宽度的总大小）。然而，这仍然是一个很困难的问题。我们提出了一种贪婪的路径排序方法，以最小化˜Tiso。
第一条路径是嵌入数最小的路径（即，arg minπ∈Pc(π)），其中P是所有路径的集合，c（π1，……，πi）是由这些路径形成的树在CPI中的嵌入数。给定一组选定的路径P，下一个路径是与P一起具有嵌入数最少的路径（即，arg minπ∈P\Pc（P∪π），或等价的arg minπ∈P\Pc（P∪π）c§）。在这里，c（P∪π）c§可以估计为c（π u）|u。C|，其中u = π.p是π到P的连接顶点，而πu是从u开始的π的后缀。直观地说，P的每个嵌入都可以扩展到c（π u）|u。P∪π的C|嵌入。
估计c(π)。回想一下，π是CPI中的一个查询路径。虽然π的嵌入没有显式地存储在CPI中，但我们可以通过动态规划算法来估计这种嵌入的数量。我们通过一个例子来说明这个动态规划算法。考虑估计图6©.中路径π =（u0、u1、u3、u7）的嵌入数对于每个顶点v∈u。C与u∈π，我们计算cu (v)，由从u开始的π后缀引起的q子图在CPI中嵌入的嵌入数，这样u被映射到v。最初，cu (v) = 1，即cu7（v18）= cu7（v19）= cu7（v20）= 1。然后，我们以自底而上的方式计算这样的数字，cu (v) = P v 0∈Nuu0(v)cu0（v0）；例如，cu3（v10）= cu7（v19）+cu7（v20）= 2。最后，c(π)=Pv∈u。C cu (v)，其中u是π的第一个顶点。运行时间与π的边对应的所有邻接列表的总大小呈线性关系。
贪婪算法。算法2给出了q的BFS树qT中所有屋顶-叶路径排序的贪婪算法。第一条路径是将该路径上的最小嵌入数与该路径上的顶点的非树状边数相贴现的路径（第2-3行）。然后，我们迭代地选择下一个路径，即一个最小化c（π u）|u的路径。C|，其中u = π.p是π到seq的连接顶点（即，π和seq之间的最后一个共享顶点）（第4-6行）。

时间复杂性。设¯Nuu0表示CPI中每对父子节点对应的邻接列表的平均总大小。然后，算法2的时间复杂度为O（¯Nuu0×（Pπ∈P|π|）），其中P是CPI中所有根到叶路径的集合，|π|是π中的边数。请注意，Pπ∈P|π|保证最多是CPI中的叶节点数乘以CPI的高度。这个时间复杂度可以通过以自底向上的方式计算π∈P的每个后缀的c（π u）来实现，如上文中的估计c(π)所述。
示例4.1：考虑图6©中的CPI和图6(d).中的核心结构有三种根-叶路径，π1 =（u0，u1，u3）、π2 =（u0，u1，u4）和π3 =（u0，u2），包括c（π1）= 4、c（π2）= 3和c（π3）= 2。由于|NT（π1）| = |NT（π2）| = 2和|NT（π3）| = 1，因此第一条路径为π2。然后，π1.p = u1、π3.p = u0、c（π u1 1）= 4和c（π u0 3）= 2。因此，第二个路径是π1与c（π u1 1）/|u1.C| = 4/3。第三条路径为π3，匹配的顺序为（u0、u1、u4、u3、u2）。

4.2.2 CPI-based Embedding Enumeration

给定一个CPI和一个匹配顺序（u1，…，u|V (q)|），G中q的嵌入被核心match枚举，其中伪代码如附录A.4节（算法5）所示。我们迭代地将每个查询顶点ui映射到一个关于匹配顺序的数据顶点。1)如果所有的查询顶点都被映射了（即，i = |V (q)|+ 1），那么我们输出嵌入。2)如果这是第一个查询顶点（即i = 1），那么我们将u1映射到CPI中的一个数据顶点v∈u1.C。3)否则，ui在匹配的顺序中有一个父ui .p，并且ui .p被映射到M（ui .p）；ui的候选从CPI中的邻接列表Nu u i i .p（M（ui .p））中获得，我们每次将ui映射到每个候选对象，然后继续到下一个查询顶点ui+1。
备注。我们不使用TurboISO [8]中的查询图压缩技术来压缩核心结构。这是因为对于我们实验中测试的随机生成的查询，它们的共重组很难被压缩；例如，核心结构平均只能减少不到1个顶点（即，大多数核心结构不能被压缩）；见附录中的表4。

4.3 CPI-based Forest-Match

我们的基于cpi的森林匹配类似于第4.2节中的核心匹配，只是森林结构可能由多个连接的树组成。还请注意，森林结构没有非树形边。根据第4.2节中的路径排序策略，我们首先估计每棵连接树在CPI中的嵌入数，然后根据连接树的嵌入数按递增顺序排序；然后用算法2对每根连接树中的根到叶路径进行排序。这样，我们就得到了森林结构中查询顶点的匹配顺序。
森林结构的嵌入枚举算法类似于算法5中的核心匹配，只是我们不需要进行非树的边缘检查。因此，数据图G不被探测为森林匹配。我们省略了这些算法的细节。
备注。我们不使用TurboISO [8]中的压缩技术来压缩森林结构，因为查询q中的森林结构不能基于下面的引理进行压缩。
引理4.2：TurboISO[8]中用于压缩查询q的压缩技术不能压缩q的森林结构。也就是说，在森林集中没有两个顶点具有相同的标签和相同的邻域。

4.4 CPI-based Leaf-Match

在本小节中，我们提出了一种有效的枚举叶集VI的所有嵌入的技术，并给定了核心集VC的嵌入MC和森林集VT的嵌入MT。请注意，VC∪VT∪VI = V (q)。基于MC和MT，我们首先为每个查询顶点u∈∈计算一个候选集C (u)。具体来说，C (u) = Nu u.p（M（u.p））\（MC∪MT）；也就是说，C (u)是C (u)是Nu u.p (v)邻接列表中的顶点集，不包括MC∪MT中使用的顶点，其中v = M（u.p）是MC∪MT中=映射到的数据顶点。请注意，C (u)⊆u。c，u。C是CPI中u的候选集。例如，在图6中，VI = {u7、u8、u9、u10}。假设u3（= u7.p）、u4（= u8.p）、u5（= u9.p）、u6（= u10.p）分别映射到v12、v5、v13、v16，然后是C（u7）= {v18、v19}、C（u8）={v21、v22}、C（u9）= {v21、v23}、C（u10）={v26}。
然后，我们的技术是基于以下引理。
引理4.3：对于VI中的任意两个查询顶点u和u0，如果u和u0的标签不同（即lq (u)，lq（u 0）），则C (u)∩C（u 0）=∅。
因此，我们根据VI的查询顶点将它们的标签划分为标签类。标签与标签类，表示S，由所有顶点的VI标签，我们表示的标签类的VIS后生成所有嵌入每个标签类SS，VI的嵌入的嵌入可以作为笛卡尔积嵌入所有不同的标签类。例如，继续上面的示例，有两个标签类，S G = {u8，u9}和S F = {u7，u10}。在生成这两个标签类M（u8、u9）= {（v21、v23）、（v22、v22、v221）、（v22、v23）}和M（u7、u10）= {（v18、v26）、（v19、v26）}后，我们得到了|M（u8、u9）|×|M（u7、u10）| = 3×2 = 6嵌入。
为标签类生成嵌入。首先，我们将Sa中具有相同父级的所有顶点合并为邻域等价类（NEC）顶点。注意，这些NEC顶点与TurboISO [8]中的压缩技术获得的顶点完全相同；也就是说，一个一次顶点只能与另一个一次顶点在同一个NEC中。此外，同一NEC中的所有顶点都有相同的候选点集。因此，我们将处理这个包含NEC顶点的更新的标签类Sa。
我们根据Sa的所有候选顶点（即|C (u)|）的数量按递增的顺序进行排序，然后根据这个顺序迭代地将每个查询顶点u映射到C (u)中的一个数据顶点。注意，对于基数|u 0 |的NEC顶点u0（即包含|u 0 |查询顶点），我们将u0映射到C（u 0）的|u 0 |顶点的组合，而不是排列。如果需要，可以通过在每个NEC顶点中排列查询顶点的映射来获得所有嵌入的集合。
与TurboISO [8]中的压缩技术相比，我们不仅考虑了NEC顶点，而且还将所有具有相同标签的叶查询顶点放在一起（即标签类）。注意，只有具有相同标签的查询顶点可能相互冲突，即不允许将两个具有相同标签的查询顶点映射到同一映射中的相同数据顶点。因此，通过将具有相同标签的查询顶点放在一起，我们就能够在早期阶段修剪没有希望的部分嵌入。
备注。注意，叶集VI的概念可以推广到q的查询顶点的独立集（即在独立集的任何两个顶点之间没有边）。然而，我们证明了叶集VI是q的森林结构的最大可能的独立集；详情见附录中的A.5节。

5. CPI CONSTRUCTION

在本节中，我们开发了一种有效的构建小型和可靠的CPI的技术。自构造最小的声音CPI是np困难引理4.1，我们提出一个启发式的方法构建CPI在两个阶段：自上而下的建设（见5.2节）和自下而上的细化（见5.3节），树边和非树边被利用修剪查询的假阳性候选顶点（见5.4节）。下面，我们首先在第5.1节中介绍我们的CPI构造算法的一般思想。

5.1 General Idea

CPI是关于q的BFS树qT构造的。qT的根顶点r的选择在附录中的A.6节中进行了讨论。然后，将q的顶点按照它们的BFS水平进行划分，其中在qT中，一个顶点的BFS水平是1加上它到r的距离；q的边被划分为树边和非树边。非树状边的进一步分类如下。
定义5.1：对于q中关于qT的非树边（u，u 0），如果u和u0在uT中处于相同的BFS级别，则（u，u 0）称为同级非树边（S-NTE）；否则（u，u 0)称为跨层非树边（C-NTE）。
例如，考虑图7(a).中的查询q假设u0为根顶点，BFS树qT如图7(b)所示，非树边为（u1、u2）和（u2、u3），其中（u1，u2）是一个S-NTE，（u2，u3）是一个C-NTE。
在第4.1节之后，我们的CPI构造的一般思想是计算候选集u。q中的每个顶点∈，而G中的诱导边在∈之间。C和u0的顶点。C在CPI中被存储为一个邻接列表Nu u 0 (v)，关于qT的树边（u，u 0）。因此，主要的问题是构建一个健全的CPI，使u。对于每个u∈V (q)尽可能小。然而，我们在引理4.1中证明了这是np困难的。因此，我们提出了一种构造小CPI的启发式方法。
一个数据顶点v可以从u中修剪出来。如果在q中存在u的邻域u0，这样u0。C在G中不包含v的任何邻域。C ∩ NG (v) = ∅).
同样，u。C可以得到为u0中顶点的标签lq (u)的邻居集的交集。C表示所有u0∈Nq (u)。
因此，根据上述一般思想，我们建议分两个阶段来构建CPI：自上而下的构建和自下而上的细化，这将在下面的两个小节中讨论。

5.2 Top-Down Construction

给定查询q的BFS树qT，CPI是通过逐层访问查询顶点来构造的，其中我们还利用非树边的修剪能力来修剪不希望的候选对象。该算法如算法3所示。
首先，我们得到了根查询顶点r的候选顶点，它是G中具有标记lq ®和度至少为dq ®的顶点，并通过了候选验证（CandVerify）（行1-2）。随机验证基本上验证一个数据顶点是否符合查询顶点的局部特征，这在附录的A.6节中讨论。我们将r标记为已访问的，并将G（第3行）中的所有顶点v的v.cnt设置为0，其中v.cnt稍后将用于确定一个顶点是否属于候选顶点。
然后，我们逐级处理查询顶点（第4-28行），对于同一级别的查询顶点，我们1)首先生成它们的候选对象集，2)然后修剪向后处理的候选对象，3)最后构建查询顶点及其父对象对应的邻接列表。假设在lev水平上的顶点集为Vlev。
1)正向候选人一代。在正向处理中，我们根据Vlev中的顺序来处理查询顶点。在处理查询顶点u时，让u。N表示q中u和u的访问邻域的集合。UN表示q中u与qT中u处于相同BFS级别的未访问邻居的集合。u.UN在第7-9行获得，将用于向后处理（参见第20行）。设置u。u的候选顶点的C是由u中的候选顶点集合生成的。N（第11至16行）。直观地说，一个数据顶点v在u中。C仅当为每个u0∈u。N，有一个数据顶点v0∈u0。邻近v的C。为了实现这一点，我们为G中的每个数据顶点维护一个计数器v.cnt，以计算u中与v相邻的访问查询邻居的数量。顶点的计数器（即v.cnt）在第11-13行进行更新，Cnt记录了u中查询顶点的数量。N（第14行）。候选人的u。C是满足v.cnt = Cnt的顶点集合，也通过随机验证（第15-16行），遵循引理5.1。然后我们将u标记为访问，对于每个具有正计数的顶点v（即vcnt>0）将vcnt重置为0（第17行）。注意，要重置v.cnt，我们只需要访问那些顶点。
引理5.1：通过算法3的第6-14行，一个标记为lq (u)的数据顶点v在u0中有一个邻域。C表示每个u0∈u。N当且仅当v.cnt=Cnt（即，第15行）。
2)向后候选人修剪。在向后处理中，我们再次应用引理5.1来过滤每个查询顶点u基于其未访问的邻居集(即u。，在正向处理中没有被利用。与正向处理相比，现在我们以相反的顺序处理查询顶点Vlev（第18-23行）。对于每个u∈Vlev，我们应用引理5.1；一个顶点v∈u。如果v.cnt，|u，C将被修剪。UN|（第21-22行）。
3)邻接列表建设。在每个查询顶点u∈Vlev被分配了一个集合u之后。在候选项中，构造了树边（上，u）对应的邻接列表，其中上= u.p是qT中u的父节点（第26-28行）。对于每个数据顶点v∈以上。C，构造了一个邻接列表Nu up (v)，它是u中的数据顶点集。连接到v的C；即，Nu up (v) = {v 0∈u。C |（v，v 0）∈E(G)}（第27-28行）。请注意，向上。C已经在迭代中被构造出来，用于处理在lev−1级别上的查询顶点。

示例5.1：考虑图7(a)中的查询q和图7(b)中的BFS树，其中u0是根顶点。然后，q的顶点被划分为三个层，u0在1级，{u1，u2}在2级，u3在3级。首先，我们在第1级（即u0）上处理顶点。u0的候选集合被分配为u0.C = {v1，v2}。
其次，我们考虑第2级的顶点（即u1和u2）。1)在正向处理中，我们首先用u1处理u1。N={u0}和u1。UN = {u2}；u1.C被指定为具有标签为lq（u1）的顶点集，它们与u0.C中的一个顶点相邻，以及u1.C = {v3、v5、v7、v9}。然后，我们用u2处理u2。N={u0，u1}和u2。UN =∅；u2.C被指定为{v4、v6、v8}。请注意，尽管v10也满足引理5.1规定的要求，但由于没有u2要求的标签D的邻居，v10被验证修剪。2)在向后处理过程中，v9由于在u2.C中没有邻居，也被从u1.C中删除；回想一下u1。UN = {u2}.3)在邻接列表构造中，构造了与（u0、u1）和（u0、u2）对应的邻接列表，如图7(d).所示。
最后，我们在第3级（即u3）上处理顶点。由于在这个级别上只有一个查询顶点，所以我们只有正向处理；u3。N={u1，u2}，和u3。C={v11，v12}。顶点v13和v15分别由于在u2.C或u1.C中没有邻居而被修剪。对应于（u3.p，u3）（即（u1，u3））构建的邻接列表如图7(d).所示。

5.3 Bottom-Up Refinement

请注意，第5.2节中的自顶而下的构造算法只考虑查询顶点u的qT中的祖先（即父、父、···）来构造u。C. 因此，有可能有一个候选顶点v∈u。C在u0中没有任何邻居。C，其中u0是qT中u的子代。例如，在图7(d)中，u1.C中的v7在u3.C中没有任何邻居；或者等价地，是Nu u 3 1（v7）=∅。在本小节中，我们提出了一种自底向上的细化方法，以进一步细化查询顶点的候选对象。
算法4显示了自底向上细化的伪代码。我们以自底向上的方式处理q的查询顶点（第1行）。请注意，在这里，在相同的BFS级别上的查询顶点的顺序可以是任意的，因为我们在这个自底而上的细化过程中不考虑S-NTE。首先，在候选细化中，类似于算法3的第18-23行，我们利用u的低层邻居的候选集从u中删除不希望的候选。C（第2-7行）。然后，在邻接列表剪枝中，我们从每个邻接列表Nu u 0 (v)中删除那些不在u0中的顶点。C（第8-11行）。
示例5.2：继续示例5.1，我们对qT进行了自下而上的查询顶点的候选点细化；假设它们按u3、u2、u1、u0的顺序处理。首先，u3没有较低层次的邻居，我们什么也不做。在处理u2时，我们用u3的候选u3.C来细化候选u2.C；v8从u2中删除，因为它在u3.C中没有邻居。接下来，在处理u1时，将v7从u1.C中删除，并删除v7的邻接列表，如图7(e)所示。最后，我们处理u0；由于同样的原因，v2从u0.C中删除，并删除了v2的邻接列表。此外，我们还需要从v1的邻接列表Nu u 1 0（v1）中删除v7，因为v7不再是u1的候选项。细化后的最终CPI如图7(e)所示。

5.4 Analysis of CPI Construction

树边和非树边的修剪能力。在我们的CPI构造中（即算法3和算法4），我们利用树边和非树边以及这些边的两个方向来细化查询顶点的候选对象。也就是说，对于q中的一个查询边（u，u 0），我们利用候选的u。用u的C来细化候选项u0。C以及利用u0。C来完善u。∈；例如，如果一个候选人v∈u。C在u0中没有邻居。C，然后从u中删除v。C. 表2总结了不同处理阶段用于修剪的查询边的方向，其中方向（例如→、←、↓、↑）表示有序BFS树的单向边的方向；例如，图7(a)、u1→u2、u2←u1、u2←u1、u1↓u3和u3↑u1。实例详见章节附录中的7.A。

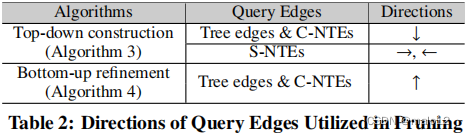
正确性。我们通过以下两个引理证明了我们的CPI构造（即算法3和算法4）的正确性。
引理5.2：对于一个数据顶点v∈V (G)和一个查询顶点u∈V (q)，如果G中有一个嵌入的∈映射到∈，那么在运行算法3后，v是u的候选(即v∈u。C).也就是说，由算法3构造的CPI是合理的。
引理5.3：给定一个良好的CPI，经过自底向上的细化（即运行算法4），CPI仍然是健全的。
时间复杂性。算法3和算法4的时间复杂度如下表所示。
定理5.1：算法3和算法4都需要时间O（|E(G)|×|E (q)|）。

6. EXPERIMENTS

我们进行了广泛的性能研究，以评估我们的基于核心-森林-叶分解的框架和我们的基于cpi的匹配算法的效率。具体来说，我们对以下现有的算法进行了评估。
•QuickSI：在[15]中的算法。
•TurboISO：[8]中最先进的算法。
•TurboISO-Boost：由[14]中的数据图压缩技术增强的TurboISO算法。
我们还评估了我们的算法的以下变体。
•CFL-Match：我们基于核心森林叶分解的算法（见第3节），由算法3和算法4构造的CPI（见第5节）（即我们的最佳算法）。
•CFL-Match-Boost：由[14]中的数据图压缩技术增强的匹配算法。
•CFL-Match-Naive：CFL-Catch算法（见4.1节）。
•CFL-Match-TD：由第5.2节中的算法3构造的CFL-Match算法。
•CF-Match：基于核心森林分解的算法（见第3节）和提出的CPI（见第5节）；也就是说，不应用森林-叶分解。
•Match：不进行查询分解的子图匹配算法，并采用所提出的CPI；即，对整个查询q应用第4.2节中的核心匹配算法。
所有的算法都是用C++实现的，并使用带有-O3标志的GNU GCC进行编译；现有算法的QuickSI [15]、TurboISO [8]和TurboISO-Boost [14]的源代码分别从他们的作者那里获得。实验是在一台拥有Intel i5 3.20 GHz CPU和8GB内存的机器上进行的。
数据集。我们评估了测试算法在实图和合成图上的性能如下。
真实的图形。我们在HPRD1、酵母和人类三个真实图上评估了算法，它们在现有的[8,12,14,22]中广泛应用。这三个图都是蛋白质相互作用网络，其中顶点标签在基因本体术语下生成。HPRD包含37,081条边，9,460个顶点，平均度为7.8,307个不同的标签。酵母包含12519条边，3112个顶点，平均度为8.1,71个不同的标签。人类是一个人类蛋白质相互作用的密集图，它包含86,282条边，4,674个顶点，平均程度为36.9，和44个不同的标签。我们还在WordNet和DBLP上测试了这些算法（见附录中的Eval-A-II），并得到了类似的结果。
合成图形。我们还生成了大型的合成数据图来评估算法。我们首先随机生成一个生成树，然后随机向生成树中添加边，而顶点标签按照幂律分布添加。合成图的默认设置为：|V(G)|=100k（即105个顶点），d(G)=8（即平均度为8）和|Σ|=50（即不同标签的数量为50）。请注意，不同标签的数量越少，就越具有挑战性。生成以下合成数据图来测试我们的算法的可伸缩性。
Vary |V (G)|：我们生成3个由G100k、G500k和G1000k表示的数据图，其中每个Gik都有ik（= i×103）顶点，默认设置为d (G)和|Σ|。
Vary d (G)：我们生成4个数据图，分别表示为Gd=4、Gd=8、Gd=16和Gd=32，其中每个Gd=i的平均度，默认设置为|V (G)|和|Σ|。
Vary |Σ|：我们生成了4个数据图，分别表示为GL=25、GL=100、GL=200，其中每个GL=i包含一个不同的顶点标签，默认设置为|V (G)|和d (G)。

查询图。通过对数据图进行随机游走，生成一个查询图作为数据图的连通子图。对于每个数据图，我们生成8个查询集，每个查询集包含100个相同大小的查询图，如表3所示。具体来说，对于HPRD、酵母和合成图，我们生成查询集q25S、q25N、q50S、q50N、q100S、q100N、q200S和q200N，其中qiS和qiN分别表示具有i个顶点的查询集，平均度≤3（即稀疏）和>3（即非稀疏）；q50S和q50N是默认查询集。对于Human，由于更高的平均度和更少的不同标签，子图匹配的数据图更困难，我们生成更小的查询集q10S、q10N、q15S、q15N、q20S、q20N、q25S和q25N，默认为q15S和q15N。
#Embeddings.我们改变了要报告的嵌入的数量，从103到105和108，默认为#嵌入= 105。请注意，嵌入的总数可能要大得多。
指标。对于每个测试，我们为一个查询集运行一个算法，其中包含100个查询图，共三次，并以毫秒为单位报告处理每个查询图的平均CPU时间。请注意，我们将处理查询集的时间限制设置为5小时（即1.8×107 ms）。如果一个算法不能在时间限制内完成，那么我们将其处理时间绘制为“INF”。

6.1 Comparing with Existing Techniques

在本小节中，我们将评估基于现有的算法，即QuickSI、TurboISO和TurboISO-Boost。请注意，我们还使用作者在[14]中提供的源代码对测试的图形运行TurboISO-Boost；但是，对于大多数查询，它不能在时间限制内完成，即使对于它可以完成的情况，它也比TurboISO慢得多（参见附录中的图21）。显然，在TurboISO-Boost的源代码中存在一些实现问题。我们已经通过电子邮件与[14]中的作者进行了沟通，但这个问题无法解决。因此，我们在下面的比较中省略了TurboISO-Boost，以公平[14]中的作者。然而，我们在[14]中实现了这些技术，并结合了我们的技术，作为CFL匹配的增强版本，并在Eval-IV中进行了评估。

Eval-I: Against Existing Algorithms by Varying |V(q)|

我们通过改变|V (q)|的总处理时间、嵌入枚举时间和查询顶点排序时间来评估现有算法的CFL-Match。嵌入枚举时间是在获得查询顶点的匹配顺序后枚举嵌入的时间，而查询顶点排序时间是计算匹配顺序和计算匹配顺序所需的其他辅助数据结构的时间。

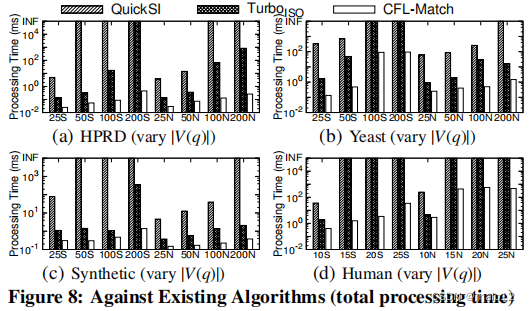
总处理时间。图8显示了每个查询图的平均总处理时间。一般来说，所有这三种算法在较大的查询中运行的速度都较慢，而QuickSI和TurboISO可能无法在大型查询的时间限制内完成（在图中表示为“INF”）。CFL-Match始终优于TurboISO，后者的表现优于QuickSI。这是由于我们通过推迟笛卡尔乘积的新框架，以及我们基于cpi的查询顶点的有效排序。我们的CFL-Match算法比最先进的算法TurboISO改进了3个数量级以上（见图8(a)中的查询q200N），甚至排除了TurboISO不能在时间限制内完成的情况。
嵌入枚举时间。图9显示了三种算法在HPRD和合成图上的嵌入枚举时间。由于QuickSI和TurboISO无法在这两个图上的大多数查询的时间限制内完成，因此我们忽略了关于酵母和人类的结果（见图8）。CFL-Match所有枚举嵌入的查询都比TurboISO快，改进可以超过4个数量级（参见HPRD上的查询q200N）；QuickSI运行速度最慢。这证实了我们的新框架的优势，通过推迟笛卡尔乘积（见第3节），比现有的算法。

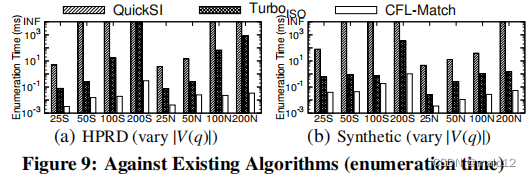
查询顶点排序时间。
我们在图10中说明了在HPRD和合成图上的TurboISO和CFL-Match的查询顶点排序时间。请注意，QuickSI的查询顶点排序时间可以忽略不计，因为排序是直接基于边缘频率的；因此，我们在图10中省略了QuickSI。我们可以看到，CFL-Match的查询顶点排序时间(|E(q)CPI构造的O（||E(G)|）时间复杂度。虽然由于路径嵌入的数量可能呈指数级，TurboISO在构建其数据结构时具有最坏的指数时间复杂度，但这两个图中的路径嵌入数量很小。因此，TurboISO在查询顶点排序时间方面也表现良好。

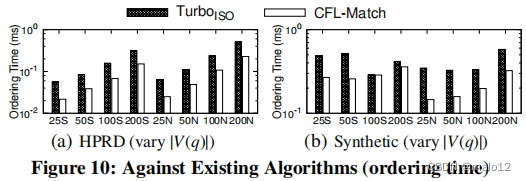
Eval-II: Evaluating Enumeration Time for Core-Structures of Queries

在这个测试中，我们评估了处理查询核心结构的算法的枚举时间。也就是说，我们的基于核心-森林-叶分解的框架对运行时间没有影响；CFL-Match相当于第4.2节中的核心匹配算法。结果如图11所示。与图9不同的是，QuickSI和TurboISO现在都可以在时间限制内完成。这是因为，1)核心结构的大小比图9中的原始查询的大小要小，以及2)核心结构的嵌入数量通常比一般查询的嵌入数量要少。CFL-Match的嵌入枚举时间比TurboISO要小得多；这证实了我们基于4.2.1节代价模型的贪婪路径排序方法计算出的更好的匹配顺序。

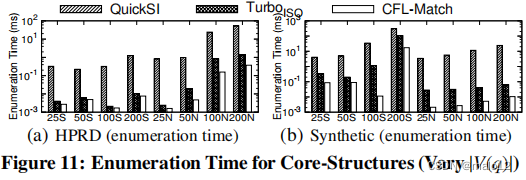
Eval-III: Varying #Embeddings

图12显示了通过改变#嵌入而得到的算法的结果。正如预期的那样，当生成更多的嵌入时，这三种算法的处理时间都会增加。然而，CFL-Match始终超过TurboISO，QuickSI表现最差。

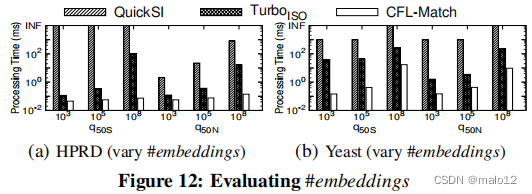
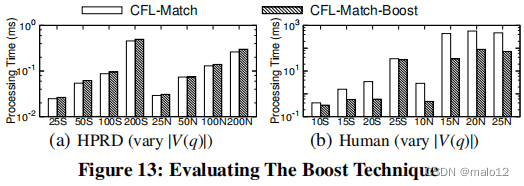
Eval-IV: Evaluating The Boost Technique in [14]

在[14]中应用助推技术的数据压缩结果图，如图13所示。由于高数据图压缩比（即约40%），boost技术改进了人类上的cfl匹配。然而，由于HPRD的低压缩比（即< 5%），CFL-Match的性能略慢；注意，依赖于查询的压缩有开销。因此，助推技术可能并不总是有帮助；我们在下面省略了CFL-Match-Boost。

6.2 Effectiveness of New Framework

在本小节中，我们将评估我们所提出的技术在减少总体处理时间方面的有效性，以及我们的CFL-Match算法的可扩展性。我们在查询集q50S（平均度≤3，表示稀疏）和q50N（平均度>3，表示非稀疏）的不同图上运行CFL-Match的变体。

Eval-V: Evaluating Our Framework

我们比较了CFL-Match与CF-Match和Match，以评估我们的基于核心林-叶分解的框架的有效性。对HPRD菌和酵母菌的检测结果如图14所示。我们可以看到，基于核心森林分解的框架（即CF-Match）改进了基于非分解的框架（即Match），而基于森林分解的框架（即CFL-Match）通过推迟笛卡尔积进一步改进了CF-Match。由于CPI中每个查询顶点的候选对象更多，因此基于酵母核心-森林-叶分解框架的笛卡尔积更大。

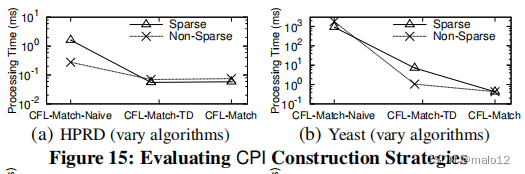
Eval-VI: Evaluating the Effectiveness of CPI Construction Strategies

不同CPI构建策略对CFL-Match算法总处理时间影响的评价结果如图15所示。天真构建的CPI（见4.1节）显著降低了CFL-Match的性能，因为CPI中查询顶点的假阳性候选。CFL-Match-TD通过自上而下的方式构建CPI（见第5.2节）改进了CFL-Match-Naive，它也利用非树边进行候选剪枝。最后，自底向上的CPI重新细化（见第5.3节）进一步减少了查询顶点的候选顶点，从而导致CFL-Match的最佳性能。请注意，由于HPRD自上而下算法构建的CPI中查询顶点候选很少，在图15(a).中，CFL-Match相对于CFL-Match-TD的改进是不显著的。

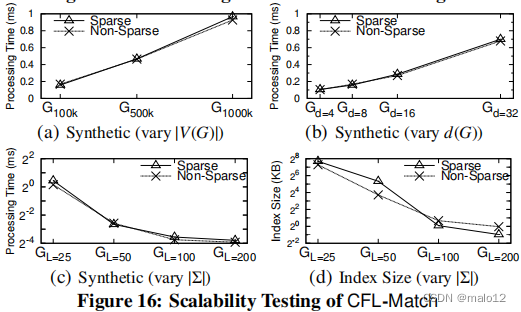
Eval-VII: Scalability Testing

我们通过改变|V (G)|、d (G)和|Σ|来测试CFL-Match在合成图上的可扩展性。不同的|V (G)|。不同的|V (G)|的结果如图16(a).所示CFL-Match的处理时间相对于|V (G)|呈线性增加。这是因为，对于合成图，查询顶点排序时间主导了嵌入枚举时间，如图9(b)和10(b).所示CPI构建的时间O（|E (G)|×|E (q)|）是查询顶点排序时间的主要因素，并且它与|V (G)|呈线性增加。变化d (G)。图16(b)显示了合成图的平均度d (G)的结果。CFL-Match的处理时间随d (G)几乎呈线性增加。这是因为d (G)越大，CPI中的边就越多，因此CFL-Match的运行时间就会越多。
变化|Σ|。图16©通过改变不同标签的数量|Σ|来说明合成图上的cfl匹配的处理时间。当|Σ|变大时，CFL-Match的处理时间减少，因为每个查询顶点的候选顶点更少，如图16(d)所示，其中索引大小（即y轴）是我们的算法构建的CPI的大小。

7. CONCLUSION

在本文中，我们提出了一个新的框架，通过基于查询的核心-森林-叶分解来延迟笛卡尔积来最小化冗余的笛卡尔积。我们是第一个解决来自“不同”顶点的笛卡尔积不希望的结果的问题。我们提出了一种新的基于路径的辅助数据结构，大小为O（|E(G)|×|V(q)|），以生成匹配顺序并进行子图匹配，显著降低了[8]中现有数据结构的指数大小O（|V(G)||V(q)|−1）。对真实图和合成图的广泛实证研究表明，我们的技术比最先进的算法多出3个数量级。作为未来可能的一项工作，将我们的核心-森林-叶分解扩展到核心结构的层次分解（例如，计算k核，（k-1）-core，…）可能是一个需要研究的有趣问题。