本文主要是介绍动态规划(算法竞赛、蓝桥杯)--区间DP石子合并与环形石子合并、能量项链,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1、B站视频链接:E28【模板】区间DP 石子合并_哔哩哔哩_bilibili
题目链接:石子合并(弱化版) - 洛谷


#include <bits/stdc++.h>
using namespace std;
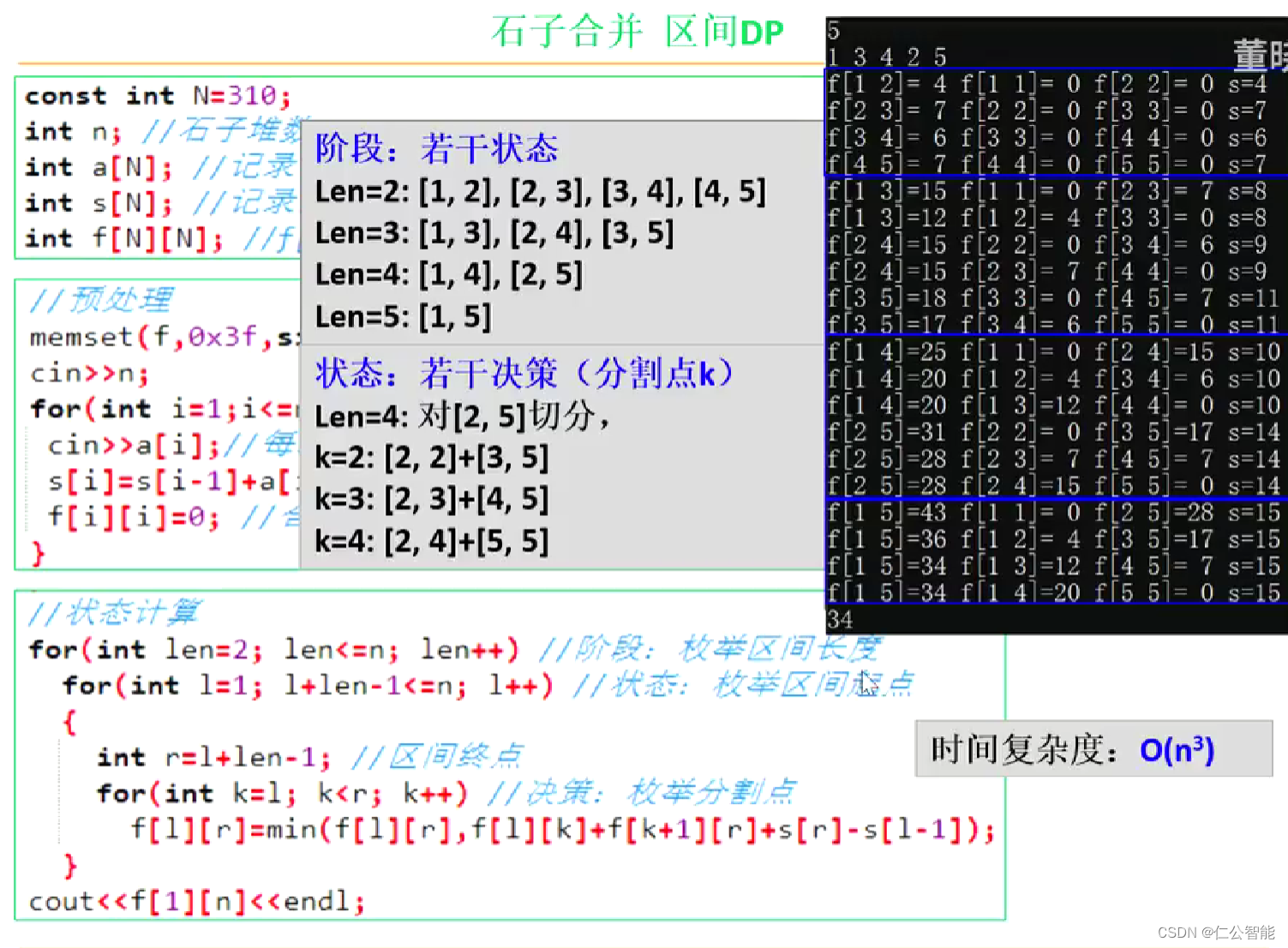
const int N=310;
int n,a[N],s[N];
int f[N][N];//f[i][j]表示从i到j合并成一堆的最小代价int main(){memset(f,0x3f,sizeof(f));cin>>n;//预处理 for(int i=1;i<=n;i++){cin>>a[i],s[i]=s[i-1]+a[i],f[i][i]=0;}//状态计算for(int len=2;len<=n;len++){//区间长度 for(int i=1,j;(j=i+len-1)<=n;i++){//区间端点 for(int k=i;k<j;k++){//区间分割点 f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+s[j]-s[i-1]);}}} cout<<f[1][n];return 0;
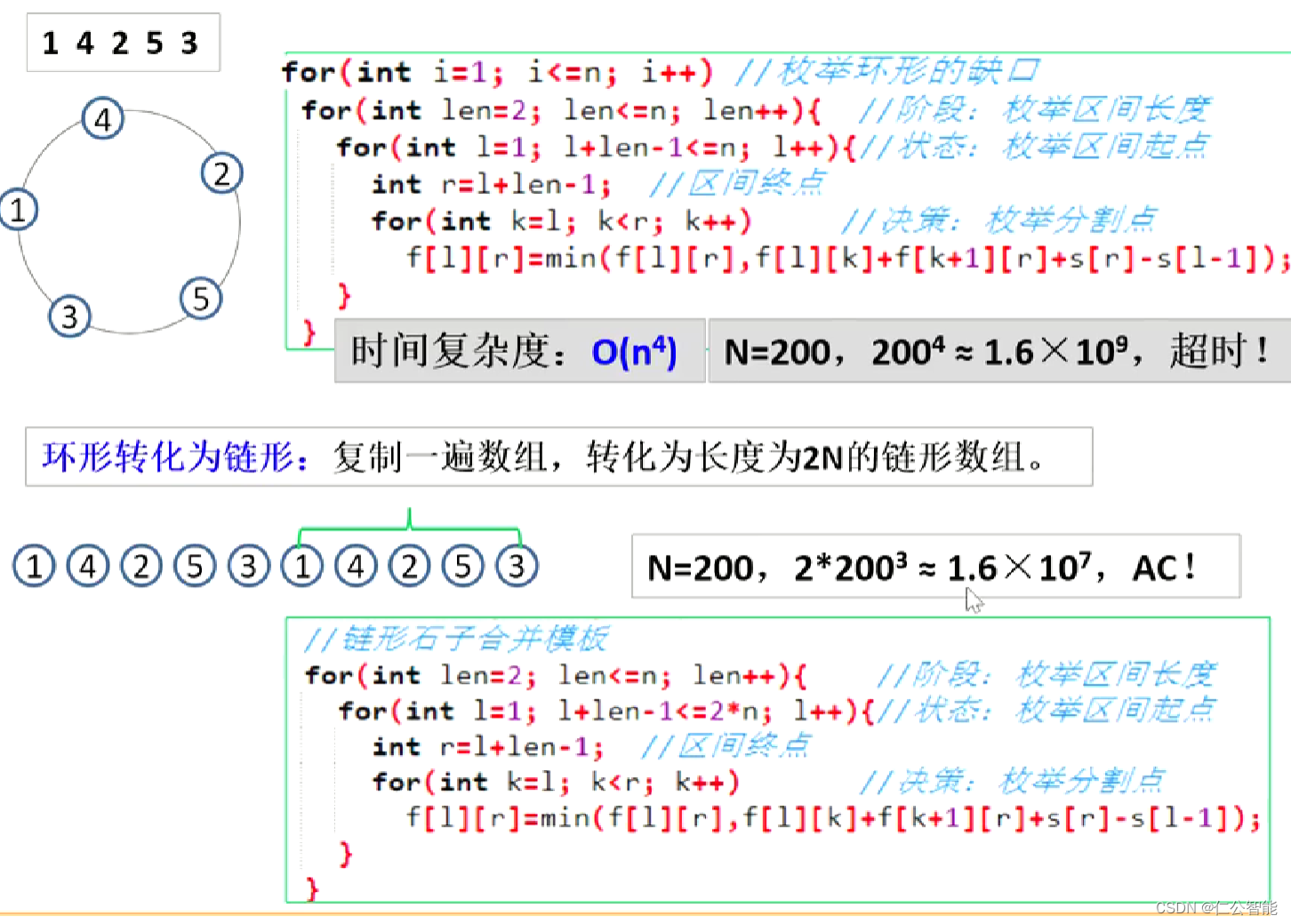
} 2、B站视频链接:E29 区间DP 环形石子合并_哔哩哔哩_bilibili
题目链接:[NOI1995] 石子合并 - 洛谷

#include <bits/stdc++.h>
using namespace std;
const int N=210;
int n,a[N],s[N];
int f[N][N];//最小值
int g[N][N];//最大值int main(){memset(f,0x3f,sizeof f);memset(g,-0x3f,sizeof g);scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&a[i]),a[i+n]=a[i];}for(int i=1;i<=2*n;i++){s[i]=s[i-1]+a[i],g[i][i]=0,f[i][i]=0;}int minv=1e9,maxv=-1e9;for(int len=2;len<=n;len++){//枚举区间长度 for(int i=1,j;(j=i+len-1)<=2*n;i++){//区间端点 for(int k=i;k<j;k++){//区间分割点 f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+s[j]-s[i-1]);g[i][j]=max(g[i][j],g[i][k]+g[k+1][j]+s[j]-s[i-1]);}minv=min(minv,f[i][i+n-1]);maxv=max(maxv,g[i][i+n-1]);}}printf("%d\n%d\n",minv,maxv);return 0;
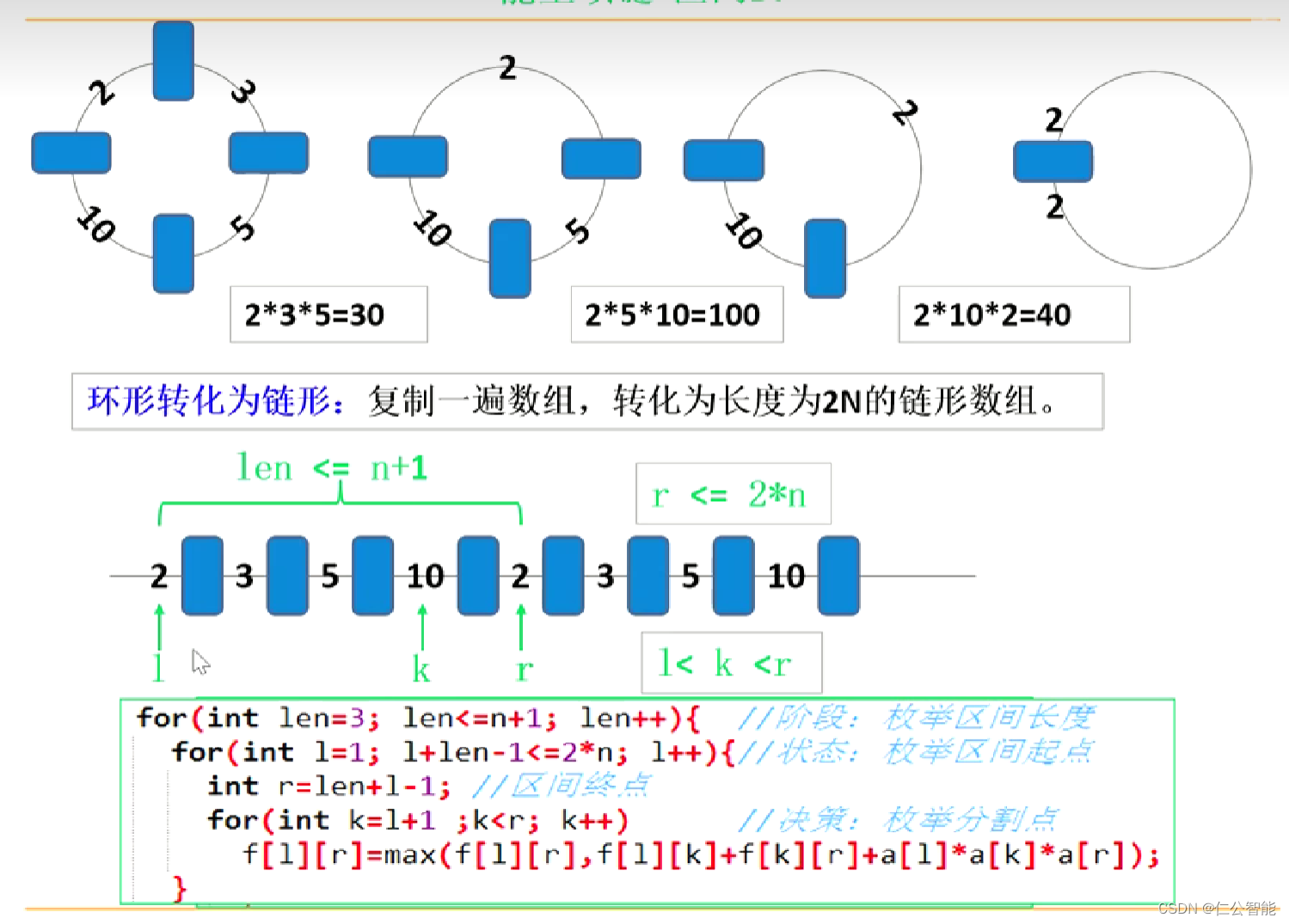
} 3、B站视频链接:E30 区间DP 能量项链_哔哩哔哩_bilibili
题目链接:[NOIP2006 提高组] 能量项链 - 洛谷


#include <bits/stdc++.h>
using namespace std;
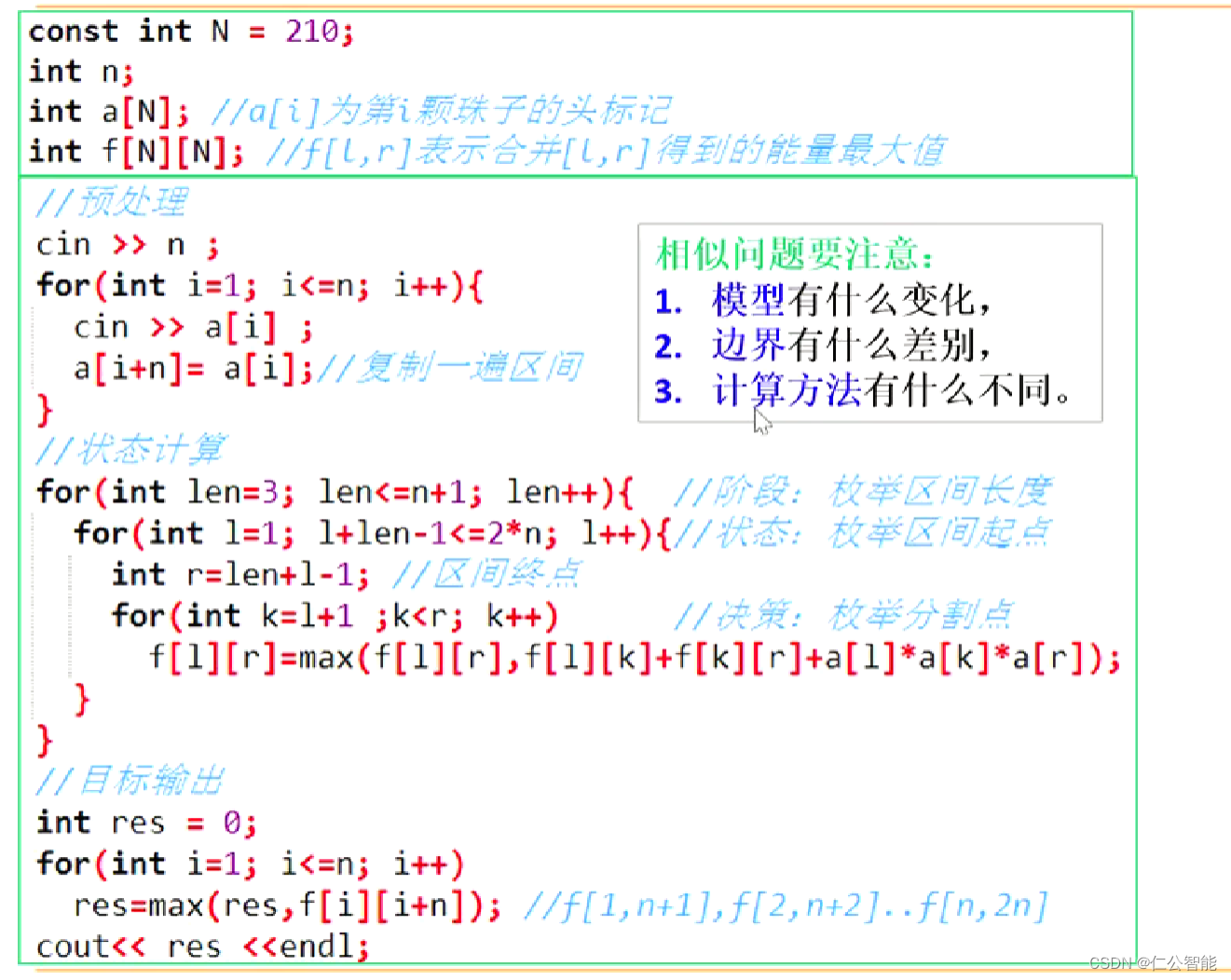
const int N=210;
int n,a[N];//a[i]为第i颗珠子的头标记
int f[N][N];//f[i][j] 表示合并[i,j]得到的最大能量int main(){cin>>n;for(int i=1;i<=n;i++)cin>>a[i],a[i+n]=a[i];for(int len=3;len<=n+1;len++){//区间长度 for(int i=1,j;(j=i+len-1)<=2*n;i++){//区间起点 for(int k=i+1;k<j;k++){//枚举分割点 f[i][j]=max(f[i][j],f[i][k]+f[k][j]+a[i]*a[k]*a[j]);}}}int res=0;for(int i=1;i<=n;i++){res=max(res,f[i][i+n]);}cout<<res<<endl;return 0;
}
这篇关于动态规划(算法竞赛、蓝桥杯)--区间DP石子合并与环形石子合并、能量项链的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





