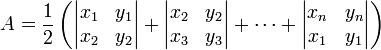本文主要是介绍洛谷 2036.PERKET,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
采用递归法的方式进行题解。
思路:首先我们知道在n种材料当中,我们需要从中选择至少有一种得配料才行。也就是说,我们选择的配料数目是自己决定的,而不是那种组合型得对于你有要求的组合型递归方式。
所以我们会想到用指数型得递归来解决这个问题。这一点需要自己首先判断明白。
第二点,我们知道,在选数得过程中我们需要根据题目的条件进行判断这种配料的酸度和苦度,因此,在我们结束递归的时候需要进行计算我们已经存储的方案得和和乘积,然后再进行相减取绝对值计算。
当然,这里也有比较坑得点,那就是,当我们在判断没有方案的时候我们需要知道,这个时候我们定义的daiti是没有发生变化的,这里为什么需要用到daiti这个变量是因为这个原因,因为乘法的累乘需要我们在初始值为1得情况下进行的,所以我需要再定义一个变脸sum1进行赋值,当daiti没有发生变化的时候,说明我们的是没有方案的。因此,这样就判断完毕了。
注意:当我们在函数中判断完毕之后,那么我们还需要知道一件事,就是在全部不选择配料的时候,这个结果我们也会放在数组里面,这个时候最终结果就是0,始终是0,这个时候我们需要找到第二个小的数,所以在找到最小的数之后赋予一个大的数,然后再继续遍历选出除最小值以外的最小数就行了。
上代码:
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
#include<algorithm>
#include<stack>
#include<queue>
#include<sstream>
#include<map>
#include<limits.h>
#include<set>
#define MAX 40
#define _for(i,a,b) for(int i=a;i<(b);i++)
#define ALL(x) x.begin(),x.end()
using namespace std;
typedef long long LL;
LL n, m, counts=1;
LL arr[MAX][MAX];
LL res = 10e9;
LL st[MAX];
LL cunchu[MAX];
void dfs(int u) {if (u > n) {LL sum1 = 0;LL daiti = 1;LL sum2 = 0;_for(i, 1, n + 1) {if (st[i] == 1) {daiti *= arr[i][1];sum2 += arr[i][2]; }}if (daiti != 1)sum1 = daiti;cunchu[counts++] = abs(sum1 - sum2);return;}st[u] = 1;dfs(u + 1);st[u] = 0;st[u] = 2;dfs(u + 1);st[u] = 0;
}
int main() {ios::sync_with_stdio(false);cin.tie(NULL); cout.tie(NULL);cin >> n;_for(i, 1, n + 1) {_for(j, 1, 3)cin >> arr[i][j];}dfs(1);LL index = 0;LL maxs = INT_MAX;_for(i, 1, counts){if (maxs > cunchu[i]) {maxs = cunchu[i];index = i;}}cunchu[index] = INT_MAX;_for(i, 1, counts) {res = min(res, cunchu[i]);}cout << res;return 0;
}当然,这是比较笨的写法,但是我们需要进行优化一下,对于dfs暴搜来说,在main函数的调用中我们需要简介一些,接下来就是在判断没有方案的时候进行优化了一下,也就是定义一个flag标志,这样在遍历的时候就能知道到底有没有方案了。
下面是优化之后的代码:
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
#include<algorithm>
#include<stack>
#include<queue>
#include<sstream>
#include<map>
#include<limits.h>
#include<set>
#define MAX 50
#define _for(i,a,b) for(int i=a;i<(b);i++)
#define ALL(x) x.begin(),x.end()
using namespace std;
typedef long long LL;
LL n, m, counts=1;
LL arr[MAX][MAX];
LL res = 10e9;
LL st[MAX];
LL cunchu[MAX];
bool flag = false;
void dfs(int u) {if (u > n) {flag = false;LL sum1 = 1;LL sum2 = 0;_for(i, 1, n + 1) {if (st[i] == 1) {flag = true;sum1 *= arr[i][1];sum2 += arr[i][2]; }}if (flag) {res = min(res, abs(sum1 - sum2));}return;}st[u] = 1;dfs(u + 1);st[u] = 0;st[u] = 2;dfs(u + 1);st[u] = 0;
}
int main() {ios::sync_with_stdio(false);cin.tie(NULL); cout.tie(NULL);cin >> n;_for(i, 1, n + 1) {_for(j, 1, 3)cin >> arr[i][j];}dfs(1);cout << res;return 0;
}这篇关于洛谷 2036.PERKET的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!