本文主要是介绍国防科大、中大0706大气科学及南信大大物院初试复习宝典——第三章:大气动力学篇,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
零、前言
本人为24考研人,一开始想考中山大学,后来改为国防科技大学,最终总分390,因为一直有用博客做笔记的习惯,考后打算将考研期间的复习笔记无偿分享出来,因为之前在一些网站上买的资料太垃圾了,又贵又垃圾实在看不惯他们,还不如自己的笔记,买资料也建议看看有无直系学长总结的资料卖,就算要钱卖的也是干货和对学弟学妹的关心,我就很幸运遇到一个真心想帮学弟学妹在中大的学长
这个系列博客包含南信大大气物理学院,中山大学或国防科技大学0706大气科学研究生初试中超全知识点,三所学校所考内容参考书目相同,但考试题型不同,国防科技大学会考计算和推导,因此南信大、中大的考试内容是国防科大考试的子集,一篇顶三校考纲
各个知识点我会将重点标出以便大家复习,标了重点的一定要回参考书目中自己再弄懂一遍
文章内容大部分来自本人啃书得到,少部分来自购买资料,基本纯手敲
如果有疏漏和错误敬请在评论中指出,欢迎大家批评指正
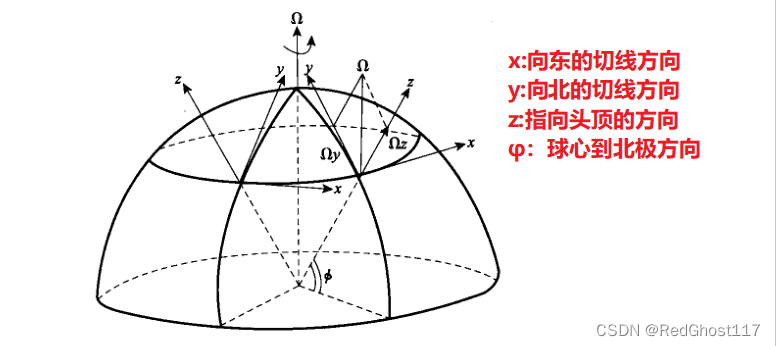
一、惯性坐标系和旋转坐标系的关系
绝对速度和地球上观察到的相对速度的关系
V a = V + Ω × r V_a=V+\Omega \times r Va=V+Ω×r
Ω \Omega Ω是地球旋转角速度,r是物体重心到地球球心的距离
对于任意矢量A,均有以下式子成立
d a A d t = d A d t + Ω × A \frac{d_a A}{dt}=\frac{dA}{dt}+\Omega \times A dtdaA=dtdA+Ω×A
则将 A a A_a Aa带入得到
d a V a d t = d V a d t + Ω × V a ; ; ; V a = V + Ω × r \frac{d_a V_a}{dt}=\frac{dV_a}{dt}+\Omega \times V_a;;;V_a=V+\Omega \times r dtdaVa=dtdVa+Ω×Va;;;Va=V+Ω×r
联立得
d a V a d t = d V d t + 2 ( Ω × V ) + Ω 2 × r \frac{d_a V_a}{dt} = \frac{dV}{dt}+2(\Omega \times V)+\Omega^2 \times r dtdaVa=dtdV+2(Ω×V)+Ω2×r
左侧是:惯性坐标系下的绝对加速度;右一是地球上观测到的相对加速度,右二是科氏项,是由于物体相对地表运动引起的加速度;第三项是由于气块随地球旋转而具有的向心加速度
二、NS方程(重点)
地球表面,大气受到的真实力有:万有引力,气压梯度力,摩擦力
在惯性坐标系中,方程写为
d V a d t = − ∇ p ρ + g ∗ + F \frac{d V_a}{dt}=-\frac{\nabla p}{\rho}+g^*+F dtdVa=−ρ∇p+g∗+F
将绝对加速度换为相对加速度,左侧只保留相对加速度,等式写为
d V d t = − ∇ p ρ + g ∗ + F − 2 ( Ω × V ) − Ω 2 × r \frac{dV}{dt}=-\frac{\nabla p}{\rho}+g^*+F-2(\Omega \times V)-\Omega^2\times r dtdV=−ρ∇p+g∗+F−2(Ω×V)−Ω2×r
万有引力和离心力和为重力,便有
d V d t = − ∇ p ρ + g + F − 2 Ω × V \frac{dV}{dt}=-\frac{\nabla p}{\rho}+g+F-2\Omega \times V dtdV=−ρ∇p+g+F−2Ω×V
三、局地变化和个别变化
个别变化展开为平流变化(F为气象要素物理量): d F d t = ∂ F ∂ t + V ⃗ ∇ F = ∂ F ∂ t + V ⃗ h ∇ F h + w ∂ T ∂ z \frac{dF}{dt}=\frac{\partial F}{\partial t}+\vec V\nabla F=\frac{\partial F}{\partial t}+\vec V_h\nabla F_h+w\frac{\partial T}{\partial z} dtdF=∂t∂F+V∇F=∂t∂F+Vh∇Fh+w∂z∂T
平时关注更多的是某地的局地变化,移向后变为 ∂ F ∂ t = d F d t − V ⃗ h ∇ F h − w ∂ T ∂ z \frac{\partial F}{\partial t}=\frac{dF}{dt}-\vec V_h\nabla F_h-w\frac{\partial T}{\partial z} ∂t∂F=dtdF−Vh∇Fh−w∂z∂T
可以看到,某物理量的局地变化=个别变化-平流变化-对流变化
四、气压梯度力(重点,会考计算)
由于气压在空间分布不均匀而作用在单位质量空气上的力
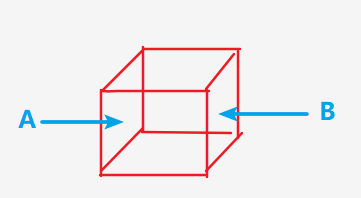
4.1 推导
- 假设从左向右为x轴正方向
- A面受到的气压产生的力为 p δ y δ z p\delta y \delta z pδyδz
- 沿着x方向有气压梯度的变化为 ∂ p ∂ x , 乘以 x 方向的一小段距离, B 处的气压为 − ( p + ∂ p ∂ x δ x ) δ y δ z \frac{\partial p}{\partial x},乘以x方向的一小段距离,B处的气压为-(p+\frac{\partial p}{\partial x}\delta x)\delta y \delta z ∂x∂p,乘以x方向的一小段距离,B处的气压为−(p+∂x∂pδx)δyδz
- 两者相加就是x方向受到的气压产生的合力,为 − ∂ p ∂ x δ x δ y δ z -\frac{\partial p}{\partial x}\delta x \delta y \delta z −∂x∂pδxδyδz
- 同理可以推得y和z方向,得到物体受到的气压梯度力的合力为 − ∇ p δ x δ y δ z -\nabla p\delta x \delta y \delta z −∇pδxδyδz
- 如果考虑的是单位质量,体积 δ x δ y δ z = 1 ρ , 则气压梯度力表示为 G = − 1 ρ ∇ p \delta x \delta y \delta z=\frac{1}{\rho},则气压梯度力表示为G=-\frac{1}{\rho}\nabla p δxδyδz=ρ1,则气压梯度力表示为G=−ρ1∇p
4.2 性质
G = − 1 ρ ∇ p G=-\frac{1}{\rho}\nabla p G=−ρ1∇p
- 气压梯度力方向是从高压向低压
- 大小与气压梯度成正比,与气体密度成反比
五、地转偏向力
由于在转动的非惯性参照系下自由运动的物体受到的一种使运动方向发生偏转的力,称为地转偏向力,它不是真实的力,是由于地球的自转产生的惯性力
5.1 理解
-
想理解这个力,先要站在上帝视角看地球自转,如果有个炮弹从赤道向极点射去,在宇宙中来看,就是赤道向北极做一个抛物线射过去

-
但是地球上的人们是跟着地球自转的,在射出那个炮弹之后,会有那个炮弹在地球上人的右手边的错觉,这个运动的改变不是由于炮弹受到了外力,而是因为人在旋转参考系中产生的错觉,因此是一种惯性力

5.2 公式
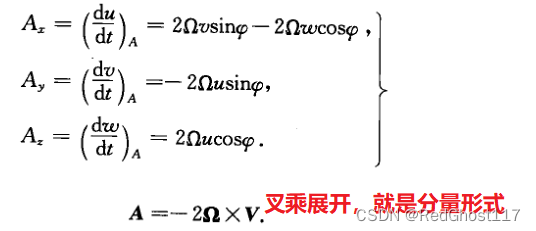
C ⃗ = − 2 Ω ⃗ × V ⃗ \vec C=-2\vec \Omega \times \vec V C=−2Ω×V
Ω \Omega Ω表示地球自转速度,该速度在x,y,z方向会有分量
之后再按叉乘的公式展开,就可以得到三个方向的地转偏向力
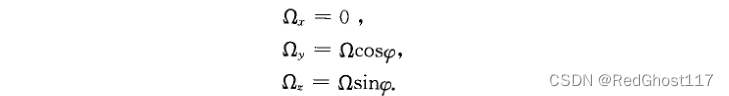
φ:当地纬度 =>由于x方向和φ方向垂直,分量为0
- 地转偏向力三个方向公式和向量形式
5.3 地转参数
一般将 f = 2 Ω s i n ϕ f=2\Omega sin\phi f=2Ωsinϕ称为地转参数
- 一般认为垂直速度相比水平速度小很多,略去x方向带有垂直速度的地转偏向力,则水平地转偏向力可以写成
C ⃗ h = f V ⃗ h × k ⃗ \vec C_h=f\vec V_h \times \vec k Ch=fVh×k
5.4 性质
- 纬度一定时,风速越大地转偏向力越大,静止的气块没有地转偏向力作用
- 风速一定时,纬度越高受到的地转偏向力越大
- 北半球地转偏向力方向指向运动方向右侧,南半球指向左侧
- 地转偏向力不改变运动速度大小只改变方向
六、流线和迹线
流线:某时刻,流线上各速度矢量线与此线相切,反映该时刻质点速度的分布情况
迹线:表示同一质点在不同时刻的位置,迹线的切线表示该质点到达这个位置时的速度方向
七、自然坐标系下的水平运动方程组
-
自然坐标系下取切线方向为S,垂直于切向向左方向为n
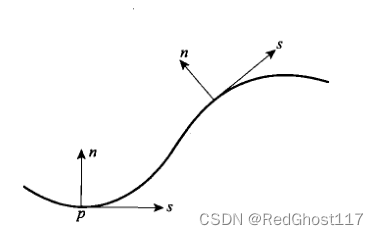
-
由此速度分解则分解为,流线方向和切线方向的速度

-
两个方向加速度对应的运动方程
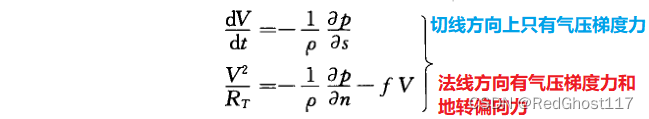
八、连续方程
根据质量守恒,气块运动过程中尽管形状和体积会发生变化,但是其质量不变
8.1 速度散度
将单位体积的体积变化率称为体胀速度,即速度散度
速度散度= ∇ ⋅ V ⃗ \nabla\cdot \vec V ∇⋅V
速度散度>0说明体积随时间变大,辐散;反之辐合
8.2 推导1:从质量守恒公式进行推导(拉格朗日观点)
质量不变即 d ( δ m ) d t = 0 = d ( ρ δ V ) d t \frac{d(\delta m)}{dt}=0=\frac{d (\rho \delta V)}{dt} dtd(δm)=0=dtd(ρδV)
将其展开得 ρ d δ V d t + δ V d ρ d t = 1 δ V d δ V d t + 1 ρ d ρ d t \rho \frac{d\delta V}{dt}+\delta V\frac{d \rho}{dt}=\frac{1}{\delta V}\frac{d\delta V}{dt}+\frac{1}{\rho}\frac{d \rho}{dt} ρdtdδV+δVdtdρ=δV1dtdδV+ρ1dtdρ
其中, 1 δ V d δ V d t \frac{1}{\delta V}\frac{d\delta V}{dt} δV1dtdδV就是单位体积的体积变化率,即体积散度
因此上式就可以写成 1 ρ d ρ d t + ∇ ⋅ V ⃗ = 0 \frac{1}{\rho}\frac{d \rho}{dt}+ \nabla\cdot \vec V=0 ρ1dtdρ+∇⋅V=0即连续方程(个别变化,为拉格朗日观点的连续方程)
8.3 推导2:从固定点的质量流入率推导(欧拉观点)
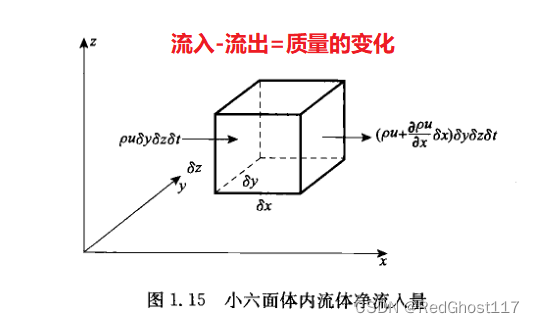
- 单位体积的净流入率=单位体积的质量增加率的公式体现
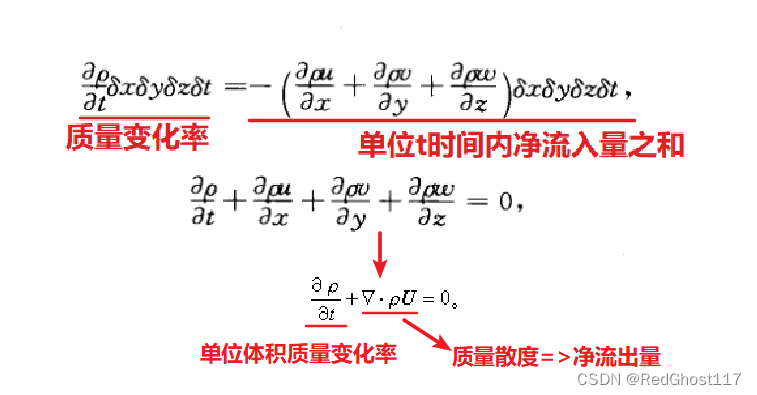
∂ ρ ∂ t + ∇ ⋅ ( ρ V ⃗ ) = 0 \frac{\partial \rho}{\partial t}+\nabla \cdot(\rho \vec V)=0 ∂t∂ρ+∇⋅(ρV)=0(局地变化,为欧拉观点的连续方程)
8.4 格朗日观点连续方程意义
1 ρ d ρ d t + ∇ ⋅ V ⃗ = 0 \frac{1}{\rho}\frac{d \rho}{dt}+ \nabla\cdot \vec V=0 ρ1dtdρ+∇⋅V=0
- 质量不变的气块,当体积增大(辐散)的时候,密度随时间减小;体积减小(辐合)时,密度随时间增大
8.5 欧拉观点连续方程意义
∂ ρ ∂ t + ∇ ⋅ ( ρ V ⃗ ) = 0 \frac{\partial \rho}{\partial t}+\nabla \cdot(\rho \vec V)=0 ∂t∂ρ+∇⋅(ρV)=0
- 由于考虑的是单位体积,由 ρ = m / V , V = 1 , 则 ρ = m \rho = m/V,V=1,则\rho=m ρ=m/V,V=1,则ρ=m
- 所以 ∇ ⋅ ( ρ V ⃗ ) \nabla \cdot(\rho \vec V) ∇⋅(ρV)表示质量散度
- 在固定点上,质量散度>0说明质量辐散,有质量流出,密度减小;反之增大
九、水平散度与垂直运动关系
9.1 不可压流体
- 如果假设 d ρ d t = 0 \frac{d\rho}{dt}=0 dtdρ=0,即密度不会改变,则为不可压流体
- 假设不可压流体,连续方程就会变为 ∂ u ∂ x + ∂ v ∂ y + ∂ w ∂ z = 0 \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0 ∂x∂u+∂y∂v+∂z∂w=0,这样水平的辐散就会造成垂直的辐合,水平的辐合会造成垂直的辐散
- 这种水平与垂直运动相互补偿的作用,可以近似研究大气的垂直运动,这种铅直运动称为系统性铅直运动
9.2 关系
将水平散度用D表示,上式积分之后就为 w 2 − w 1 = − ∫ z 1 z 2 D d z w_2-w_1=-\int_{z_1}^{z_2}Ddz w2−w1=−∫z1z2Ddz
如果z1取地面,z2取大气某层那么有 w t = − ∫ 0 z t D d z w_t=-\int_{0}^{z_t}Ddz wt=−∫0ztDdz
这个式子表示:
- 当地面到大气某层有水平辐散的话,有空气流失,有下沉运动
- 地面到大气某层有水平辐合的话,有空气补充,有上升运动
十、p坐标系与z坐标系转换关系(应该不重点,纯粹满足推导不同形式地转风使用)
由于p是z的单调单值函数,因此p与z可以互相表示,即可以写为p=p(x,y,z,t)或z=z(x,y,p,t)
对任意物理量有
F ( x , y , p , t ) = F ( x , y , z ( x , y , p , t ) , t ) F(x,y,p,t)=F(x,y,z(x,y,p,t),t) F(x,y,p,t)=F(x,y,z(x,y,p,t),t)
p不变的情况下求偏导
( ∂ F ∂ x ) p = ( ∂ F ∂ x ) z + ∂ F ∂ z ( ∂ z ∂ x ) p (\frac{\partial F}{\partial x})_p=(\frac{\partial F}{\partial x})_z+\frac{\partial F}{\partial z}(\frac{\partial z}{\partial x})_p (∂x∂F)p=(∂x∂F)z+∂z∂F(∂x∂z)p
将F换为气压则有
0 = ( ∂ P ∂ x ) z − ρ g ( ∂ z ∂ x ) p 0=(\frac{\partial P}{\partial x})_z-\rho g(\frac{\partial z}{\partial x})_p 0=(∂x∂P)z−ρg(∂x∂z)p
( ∂ P ∂ x ) z = ρ g ( ∂ z ∂ x ) p = ρ g d ϕ g d x (\frac{\partial P}{\partial x})_z=\rho g(\frac{\partial z}{\partial x})_p=\rho g\frac{d\phi}{gdx} (∂x∂P)z=ρg(∂x∂z)p=ρggdxdϕ
因此有
∇ p = ρ ∇ ϕ \nabla p=\rho \nabla \phi ∇p=ρ∇ϕ
十一、地转风(重点)
据观测,大尺度运动的水平速度量级远大于垂直运动量级,因此大尺度运动是接近水平和等速的,对自由大气可以忽略摩擦力
地转风:无加速度、无摩擦的空气水平运动称为地转风,是在水平气压梯度力和科氏力平衡时的风
V ⃗ g = − 1 f ρ ∇ h P × k ⃗ 即 \vec V_g=-\frac{1}{f\rho}\nabla_h P\times \vec k即 Vg=−fρ1∇hP×k即
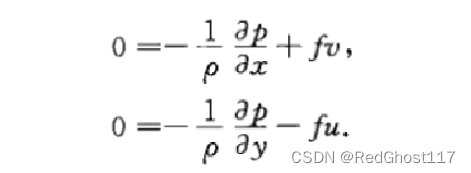
工作中分析高空等压面,使用位势梯度更多,由 ∇ h p = − ρ g 0 ∇ p H {\nabla_h p}{}=-\rho g_0 \nabla_p H ∇hp=−ρg0∇pH得到位势梯度的地转风公式(这儿是不是应该没负号)
V ⃗ g = − g 0 f ∇ p H × k ⃗ \vec V_g=-\frac{g_0}{f}\nabla_p H \times \vec k Vg=−fg0∇pH×k
将p的梯度与重力位势梯度关系带入后,可以得到p坐标系下的地转风方程
∇ p = ρ ∇ ϕ 带入得到 \nabla p=\rho \nabla_ \phi带入得到 ∇p=ρ∇ϕ带入得到
V g = − 1 f ∇ ϕ × k V_g=-\frac{1}{f}\nabla_\phi \times k Vg=−f1∇ϕ×k
11.1 性质
V ⃗ g = − 1 f ρ ∇ h P × k ⃗ \vec V_g=-\frac{1}{f\rho}\nabla_h P\times \vec k Vg=−fρ1∇hP×k
- 地转风方向和气压梯度力方向垂直,即地转风和等压线垂直
- 北半球f>0,右手法则可得地转风垂直气压梯度向右;南半球则指向气压梯度左侧
- 背风而立,低压在左高压在右
- 气压梯度力大小和纬度成反比,但只适用于中高纬度,因为低纬度地转偏向力很小,不符合地转平衡
- 气压梯度力大小与空气密度成反比,因此一般高空的地转风强于地面的
- 气压梯度力大小和气压梯度成正比
- 由地转平衡,风场可以反映气压场,气压场也可以反映风场
十二、梯度风
惯性力离心力,气压梯度力,地转偏向力三者平衡时的风,是无切向加速度,无摩擦的大气运动
由于不考虑切向加速度,则自然坐标系中只用考虑法向方向的方程,则有了梯度风方程
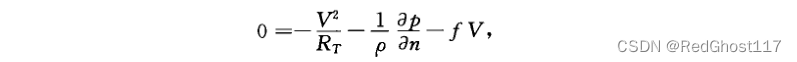
1/RT:曲率,气旋性曲率为正,反气旋为负
12.1 性质
- 地转风与气压梯度方向也垂直
- 地转风是水平气压梯度力,惯性离心力,水平地转偏向力三力平衡
- 逆时针旋转的称为气旋式梯度风,顺时针的称为反气旋式梯度风
- 定义气旋式梯度风的曲率为正
北半球气旋中心一定是低压中心
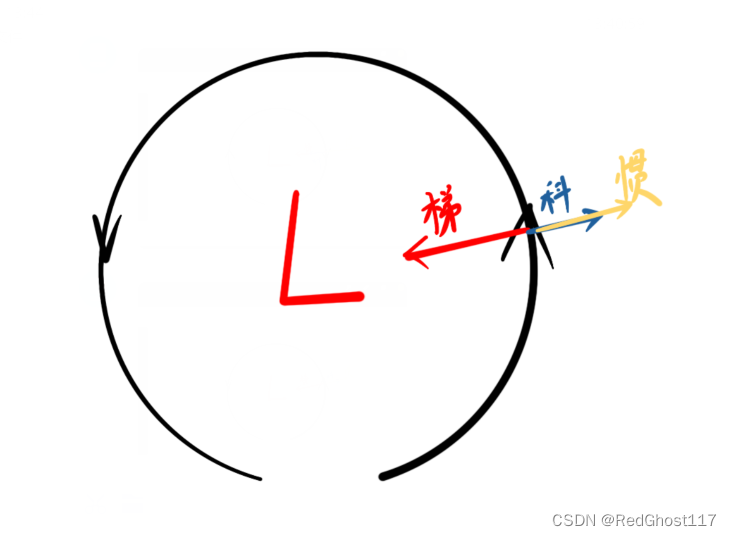
如果气旋中心是高压,将无法平衡
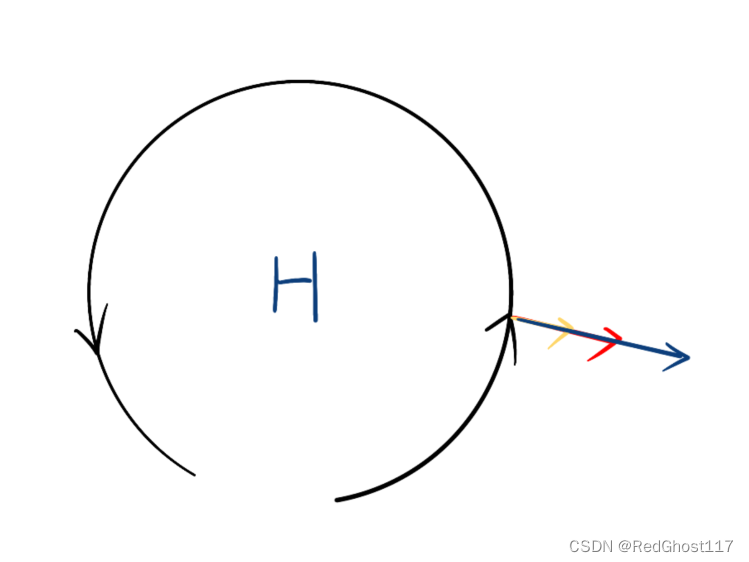
- 反气旋中心可以是低压中心或者高压中心——不同尺度天气系统可能两种都存在
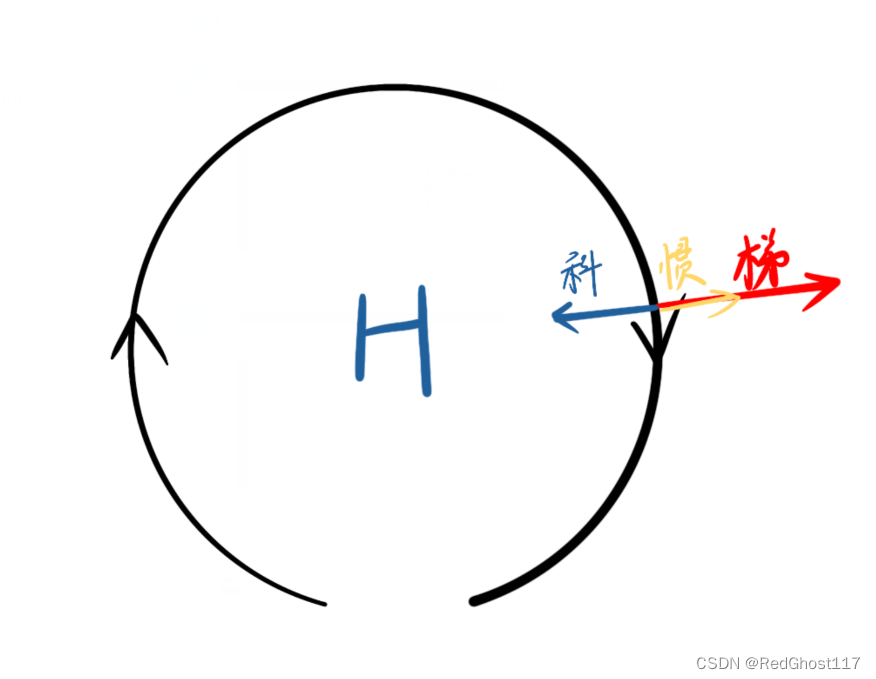
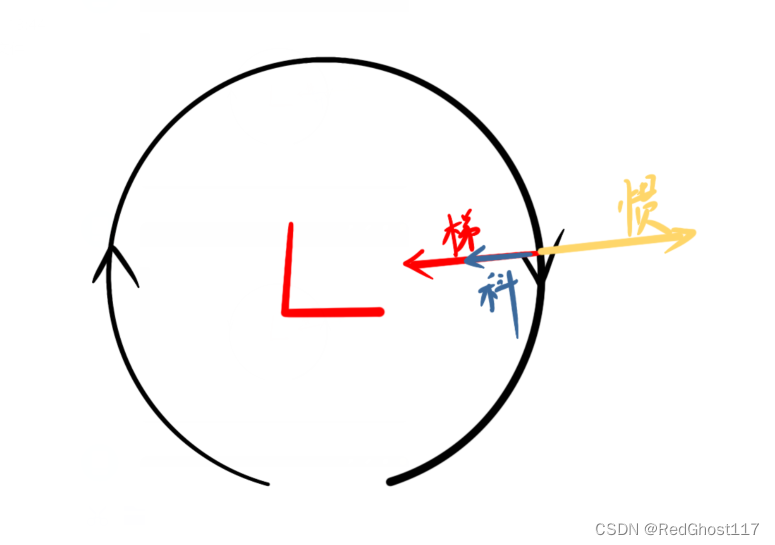
两种都可以存在,但是高压中心的反气旋更常见,中心为低压在龙卷风中可能会出现
11.2 梯度风大小
解一元二次方程得
-
解方程得梯度风风速为
V c = − f R 2 ± f 2 R 2 4 − R ρ ∂ p ∂ n V_c=-\frac{fR}{2} \pm \sqrt{\frac{f^2R^2}{4}-\frac{R}{\rho}\frac{\partial p}{\partial n}} Vc=−2fR±4f2R2−ρR∂n∂p -
对于
气旋,R>0 ,偏p/偏n<0,取减号风速才为正,有意义,同时V可以无穷大
V c = − f R 2 + f 2 R 2 4 − R ρ ∂ p ∂ n V_c=-\frac{fR}{2} + \sqrt{\frac{f^2R^2}{4}-\frac{R}{\rho}\frac{\partial p}{\partial n}} Vc=−2fR+4f2R2−ρR∂n∂p -
对于
正常反气旋R<0 ,偏p/偏n>0,数学而言取正取负都有意义,但是如果取正则有气压梯度越大,风速越小的结论,不符合事实,因此应该取负,这样V有最大值
V c = − f R 2 − f 2 R 2 4 − R ρ ∂ p ∂ n V_c=-\frac{fR}{2} - \sqrt{\frac{f^2R^2}{4}-\frac{R}{\rho}\frac{\partial p}{\partial n}} Vc=−2fR−4f2R2−ρR∂n∂p -
对于
反常反气旋(中间是低压的反气旋),则要取正才有意义
11.3 反气旋的最大风速性质(重点)

反气旋的最大气压梯度与纬度,空气密度,曲率大小成正比
因此在高纬度,冬季,曲率较小的地方高压极限气压更大
因此反气旋的外围曲率较小,等压线一般会更密集,气压梯度更大
11.4 地转风速和梯度风速大小比较
将自然坐标系下的地转风方程
V g = − 1 ρ f ∂ p ∂ n V_g=-\frac{1}{\rho f}\frac{\partial p}{\partial n} Vg=−ρf1∂n∂p
带入梯度风方程中的气压梯度项得到
V c 2 R + f V c = f V g \frac{V_c^2}{R}+fV_c=fV_g RVc2+fVc=fVg
同除以梯度风得到
V g V c = 1 + V c R f \frac{V_g}{V_c}=1+\frac{V_c}{Rf} VcVg=1+RfVc
可以看到,比值是否大于1,取决于曲率半径R是否>0
- 气旋时R>0,地转风大于梯度风
- 反气旋时R<0,地转风小于梯度风
对于中纬度大尺度系统,地转风和梯度风相差不大,可以用地转风代替梯度风,但低纬度必须用梯度风公式而不能用地转风
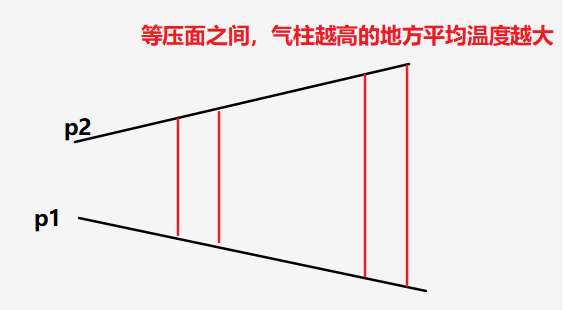
十五、气柱温度与厚度的关系
由等温大气的压高公式,可以推得一段高度范围的平均温度
T ˉ = g 0 Δ H R d l n ( p 1 / p 2 ) \bar T=\frac{g_0 \Delta H}{R_d ln(p1/p2)} Tˉ=Rdln(p1/p2)g0ΔH
可以看出,如果压强差是确定的,气柱的平均气温取决于气柱高度
由此温度梯度就可以用厚度梯度来表示
− ∇ T ˉ = − g 0 ∇ ( Δ H ) R d l n ( p 1 / p 2 ) -\nabla\bar T=-\frac{g_0 \nabla(\Delta H)}{R_d ln(p1/p2)} −∇Tˉ=−Rdln(p1/p2)g0∇(ΔH)
因此在两个等压面之间,(p1和p2不变)越厚的地方平均温度越大
十六、热成风(重点,23年计算题)
16.1 理解
- 首先假设地面有一层等压面是水平的 p 0 p_0 p0,由于与地面平行,因此气压的梯度在水平面上是0,因此没有地转风
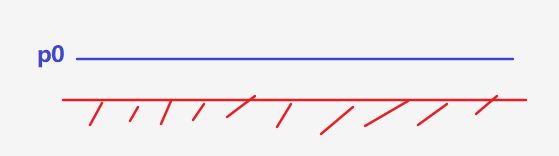
- 之后往高层发现,发现p1层处,在A点上空的厚度大,B点上空厚度小,由上文说的气层厚度与平均温度的关系,可以知道气层厚度的区别是由于平均温度不同造成,A点上空的平均温度高于B点上空
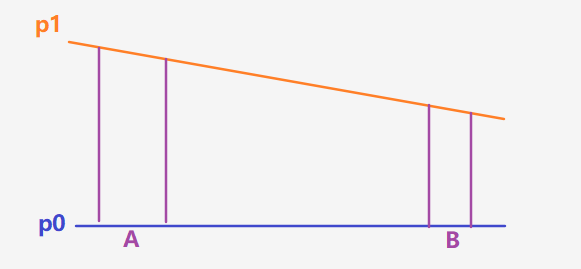
- 这样p0层就往冷区倾斜,这时候再计算气压梯度的时候发现高层存在气压梯度,有气压梯度力,存在地转风
- 这样低层地转风为0,高层不为零,高低层之间地转风产生差异,这个差异就叫热成风
16.2 公式推导(会推导不愁记不住)
上面的理解表明,热成风就是不同高度地转风的差,因此求地转风就是求地转风随高度的变化,即上层地转风和下层地转风的矢量差
V ⃗ g = − g 0 f ∇ p H × k ⃗ \vec V_g=-\frac{g_0}{f}\nabla_p H \times \vec k Vg=−fg0∇pH×k
对气压求偏导
∂ V ⃗ g ∂ p = − g 0 f ∇ p ∂ H ⃗ ∂ p × k ⃗ \frac{\partial \vec V_g}{\partial p}=-\frac{g_0}{f}\nabla_p \frac{\partial \vec H}{\partial p} \times \vec k ∂p∂Vg=−fg0∇p∂p∂H×k
之后将位势高度表示的静力方程带入
d p d H = − ρ g 0 = − p g 0 R d T \frac{dp}{dH}=-\rho g_0=-\frac{pg_0}{R_dT} dHdp=−ρg0=−RdTpg0
得到
∂ V ⃗ g ∂ p = R d f p ∇ p T × k ⃗ \frac{\partial \vec V_g}{\partial p}=\frac{R_d}{fp}\nabla_p T \times \vec k ∂p∂Vg=fpRd∇pT×k
积分后得到地转风公式
V ⃗ T = − R d f l n p 1 p 2 ∇ p T ˉ × k ⃗ \vec V_T=-\frac{R_d}{f}ln\frac{p1}{p2}\nabla_p \bar T \times \vec k VT=−fRdlnp2p1∇pTˉ×k
如果将压高公式带入,平均温度的梯度用气层厚度表示则有
V ⃗ T = − g 0 f ∇ p ( H 2 − H 1 ) × k ⃗ \vec V_T=-\frac{g_0}{f}\nabla_p (H_2-H_1) \times \vec k VT=−fg0∇p(H2−H1)×k
用重力位势表达则为
V ⃗ T = − 1 f ∇ p ( ϕ 2 − ϕ 1 ) × k ⃗ \vec V_T=-\frac{1}{f}\nabla_p (\phi_2-\phi_1) \times \vec k VT=−f1∇p(ϕ2−ϕ1)×k
16.3 性质
- 两等压面之间只要存在温度梯度,就一定存在热成风
- 叉乘判断方向,热成风方向与温度梯度(从高温到低温)垂直,即热成风方向为等温线方向
- 南北半球f相反,因此北半球热成风方向在温度梯度右侧,南半球在左侧
- 北半球,背热成风而立,低温在左高温在右
16.4 热成风随高度的变化
与等高线平行且低温对应低压
- 同一高度上温度存在梯度,但是等温线与等高线平行,且低温地区对应低压,高温区对应高压
- 这样热成风和地转风的方向是相同的,都是温度(位势高度)梯度垂直方向
- 但由于空气密度随高度减小,地转风随高度风速增加
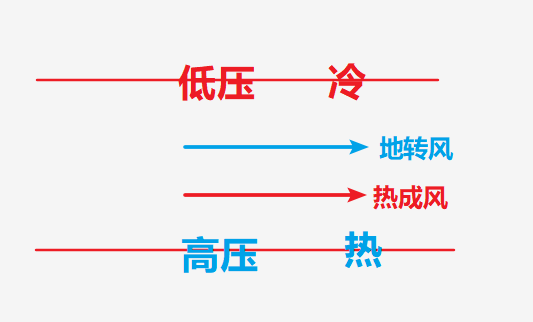
与等高线平行且低温对应高压
- 这种配置,地转风方向与地转风就是相反的
- 就是随着高度的增加,风向会向相反方向增加
- 风速还是随高度增加
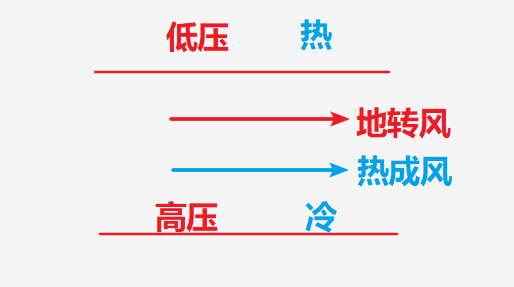
冷平流型
- 等压线和等温线是垂直的,且如图分配
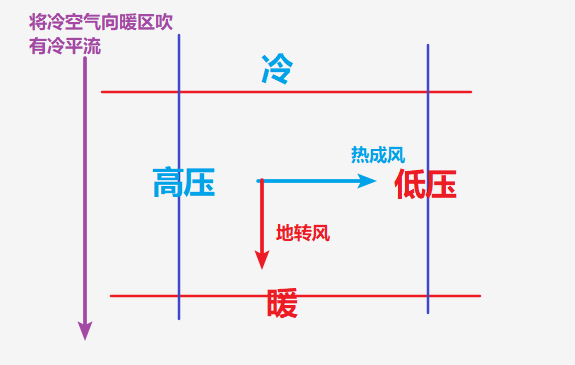
- 由此看来,低层向南的地转风叠加上向右的热成风等于高层的风方向,可见随高度增加风向逆时针旋转,风速增加
暖平流型
- 与上图的区别就是左侧为低压,右侧为高压,分析结论相反
- 风随高度顺转,风速增加,有暖平流
小结
- 温度梯度方向与位势高度梯度方向一致,则随高度风向不变化
- 温度梯度方向与位势高度梯度方向想法,则随高度风向反向
- 温度梯度与位势高度梯度方向垂直,看地转风从暖吹向冷or冷吹向暖,即为暖/冷平流
- 风随高度逆转:冷平流
- 风随高度顺转:暖平流
十七、正压与斜压大气
17.1 正压大气
这密度仅取决于气压的大气,即 ρ = ρ ( p ) \rho = \rho(p) ρ=ρ(p),于是等压面就是等密度面,由状态方程可知,等密度面就是等温面,于是 ∇ p T = 0 \nabla_p T=0 ∇pT=0因此热成风为0,地转风不随高度发生变化
17.2 斜压大气
指密度依赖于气温和气压,即 ρ = ρ ( p , T ) \rho = \rho(p, T) ρ=ρ(p,T),等压面与等密度面(等温面)有交角, ∇ p T ≠ 0 \nabla_p T \ne 0 ∇pT=0,存在热成风
这篇关于国防科大、中大0706大气科学及南信大大物院初试复习宝典——第三章:大气动力学篇的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!