本文主要是介绍时间序列分析——自回归移动平均(ARMA)模型,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、时间序列与ARMA模型
自回归滑动平均模型(ARMA模型,Auto-Regression and Moving Average Model)是研究时间序列的重要方法,由自回归模型(AR模型)与滑动平均模型(MA模型)为基础“混合”而成,具有适用范围广、预测误差小的特点。
一般p阶自回归过程AR(p)是:
(1-1)
其中{}为白噪声,
为自回归模型的参数。若用滞后算子L表示,则式(1-1)可以用滞后算子的p阶多项式来描述。
(1-2)
其中,称为特征多项式或自回归算子。
如果时序{}满足方程:
(1-3)
则称{}为q阶滑动平均过程,简写为MA(q)。其中{
}为白噪声,
为滑动平均模型的参数。
自回归移动平均过程具有随机性的特点,它包括了两个不同的部分,即自回归、移动平均。如果前p代表一部分的阶数值的上限值,用q代表后一部分的阶数值的上限值,那么自回归滑动平均过程就可以表示为ARMA(p,q)。具体表达式如下:
(1-4)
其中{}为白噪声,
为自回归模型的参数,
为滑动平均模型的参数。
二、ARMA模型的建立
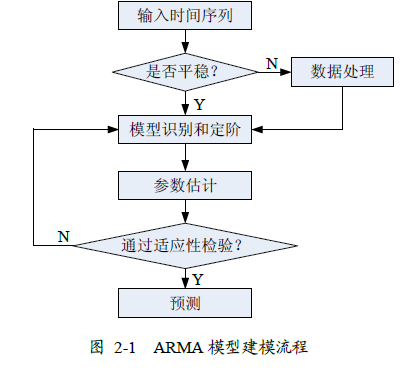
ARMA建模步骤
(1)对输入的数据进行判断,判断其是否为平稳非纯随机序列,若平稳则直接进入步骤2;若不平稳则进行数据处理,处理后才能进入步骤2。
(2)通过自相关和偏自相关函数,并结合AIC或BIC准则对建立的模型进行模型识别和定阶。
(3)完成模型识别和定阶后,进入模型的参数估计阶段。
(4)完成参数估计后,对拟合的模型进行适应性检验。如果拟合模型通过检验,则开始进行预测阶段。若模型检验不通过,则重新进行模型识别和检验,即重复步骤2,重新选择模型。
(5)最后,利用适应性高的拟合模型,来预测序列的未来变化趋势。
数据的平稳性检验与处理
假如时间序列符合下列要求:(1)对任意时间t,其均值恒为常数;(2)对于任意的时间t与s,此时间序列的相关系数是由两个时间点之间的时间段决定的,两个时间点的起始点不会造成任何影响。这样的时间序列就是平稳时间序列。
若一个AR过程是一个平稳过程,则其特征方程的根绝对值应在单位圆之外;而MA过程包含一组有限的、平稳的白噪声的线性组合,因此,MA过程是“天生”平稳的。ARMA模型可以看成是AR模型和MA模型的组合,而MA过程必定是平稳的。所以,ARMA模型的平稳性只需检验AR部分的平稳性。
平稳性检验的方法有数据图、逆序检验、游程检验、单位根检验、DF检验、ADF检验等。
在实际中,常常会遇到输入的时间序列经检验是非平稳的,这样就无法采用ARMA模型,通常的处理方法是采用差分的方法将它们变换为平稳的。经差分后,如果时间序列检验为平稳,就对差分后的时间序列进行处理,便可建立对应的平稳随机过程或模型。一个非平稳时间序列接受了d次差分处理并成为平稳序列时,就能够用一个平稳的ARMA(p,q)模型当作其对应的模型,则称该原始时间序列是一个自回归积分滑动平均时间序列,表示成ARIMA(p,d,q)。
模型识别和定阶
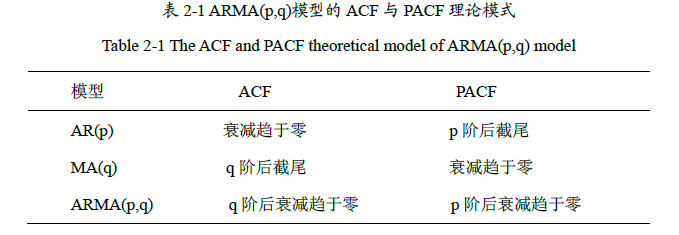
模型的识别方法一般有两种,一种是自相关函数(ACF),另一种是偏自相关函数(PACF)。这两种方法是识别ARMA模型最有效的方法。可以采用两种函数的截尾性质来判断该模型的类型。
使用自相关函数和偏自相关函数的截尾来判断模型为ARMA模型时,并不能确定p和q的阶数,为了比较精确的确定p和q的阶数,就必须与常用的定阶准则联合起来应用。如今应用最为广泛的是AIC(最小信息量准则(A-Information Criterion))和BIC准则。
AIC准则是拟合精度和参数个数的加权函数,使AIC函数达到最小值的模型被认为是最优模型。设{}为一时间序列的样本,我们用AR(n)模型来描述它。
是拟合残差方差,定义AIC准则函数如下:
(2-1)
(2-2)
其中M(N)等于 或
,我们便取
为最佳自回归模型阶数。
BIC准则定义如下:
(2-3)
其中,n为参数个数。若某一阶数满足
(2-4)
其中M(N)等于 或
,则
为最佳系数。
模型参数估计和适应性检验
任何ARMA或MA过程可以用一个无限阶的AR过程表示,所以如果选择了一个不合适的模型,但只要模型的阶数足够高,它仍然能够比较好地逼近被建模的随机过程。在这三种参数模型中,AR模型得到了普遍应用,其原因是AR模型的参数计算过程是线性方程,比较简便。MA模型一般需要数量很多的参数;ARMA模型虽然所需的参数数量最少,但参数估计的算法是非线性方程组,其运算远比AR模型复杂。再考虑到任意ARMA或MA信号模型可以用无限阶或阶数足够大的AR模型来表示,我们就将ARMA模型转换为AR模型,并用Bury递推算法求解参数。详见点击打开链接。
这篇关于时间序列分析——自回归移动平均(ARMA)模型的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!