本文主要是介绍[深度学习]Part2(线性)回归算法Ch03——【DeepBlue学习笔记】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本文仅供学习使用
(线性)回归算法Ch03
- 1. 回归算法
- 1.1 线性回归
- 1.2 回归算法理性认知
- 1.2.1 线性回归、最大似然估计及二乘法
- 1.2.2 最小二乘法的参数最优解
- 1.2.3 最小二乘法的算例
- 1.3 目标函数(loss/cost function)
- 1.4 模型
- 1.4.1 多项式拓展——升维(欠拟合)
- 1.4.2 线性回归的过拟合——提前停止
- 1.4.3 Ridge回归
- 1.4.4 LASSO回归——特征选择
- 1.4.5 Elasitc Net
- 1.5 模型效果判断
- 2. 代码实例
- 2.1 线性回归伪代码
- 2.2 波士顿房屋价格预测
- 2.2.1 原始数据——欠拟合
- 2.2.2 原始数据——多项式拓展(Linear)/ Ridge回归 / LASSO回归
- 2.2.3 忽略警告
- 3. 机器学习调参
- 4. 线性回归总结
1. 回归算法
回归算法是一种有监督算法 .回归算法是一种比较常用的机器学习算法,用来建立“解释”变量(自变量X) 和观测值(因变量Y)之间的关系;从机器学习的角度来讲,用于构建一个算法模型(函数)来做属性(X)与标签(Y)之间的映射关系,在算法的学习过程中, 试图寻找一个函数 h : R d → R h:{{R}^{d}}\to R h:Rd→R 使得参数之间的关系拟合性最好。 回归算法中算法(函数)的最终结果是一个连续的数据值,输入值(属性值)是一个d维度的属性/数值向量
from sklearn.linear_model import LinearRegression
1.1 线性回归
线性回归是机器学习中最简单的有监督学习算法之一。
h θ ( x ) = θ 0 + θ 1 x 1 + . . . + θ n x n = ∑ i = 0 n θ i x i = θ T x {{h}_{\theta }}(x)={{\theta }_{0}}+{{\theta }_{1}}{{x}_{1}}+...+{{\theta }_{n}}{{x}_{n}}=\sum\limits_{i=0}^{n}{{{\theta }_{i}}{{x}_{i}}}={{\theta }^{T}}x hθ(x)=θ0+θ1x1+...+θnxn=i=0∑nθixi=θTx ((1,n+1),(n+1,1))
最终要求是计算出 θ 的值,并选择最优的 θ 值构成算法公式(x0=1,则包含截距项,相当于多了一列特征x0,此时需要拓展一列特征;若为0,则不包含截距项,不需拓展)
认为数据中存在线性关系,也就是特征属性X和目标属性Y之间的关系是满足
线性关系。
在线性回归算法中,找出的模型对象是期望所有训练数据比较均匀的分布在直线或者平面的两侧。
在线性回归中,最优模型也就是所有样本(训练数据)离模型的直线或者平面距离最小。
线性回归问题中一个设计恰当的特征(或者特征集),应该能为原始特征空间提供好的非线性拟合,与此同时也能为经过转换的特征空间提供好的线性拟合。
1.2 回归算法理性认知
1.2.1 线性回归、最大似然估计及二乘法
y ( i ) = θ T x + ε ( i ) {{y}^{(i)}}={{\theta }^{T}}x+{{\varepsilon }^{(i)}} y(i)=θTx+ε(i)
误差 ε ( i ) ( 1 ≤ i ≤ n ) {{\varepsilon }^{(i)}}(1\le i\le n) ε(i)(1≤i≤n) 是独立同分布的,服从均值为0,方差为某定值 σ 2 {{\sigma }^{2}} σ2 的高斯分布——中心极限定理
实际问题中,很多随机现象可以看做众多因素的独立影响的综合反应, 往往服从正态分布
- 似然函数
p ( ε ( i ) ) = 1 σ 2 π e − ( ε ( i ) ) 2 2 σ 2 p({{\varepsilon }^{(i)}})=\frac{1}{\sigma \sqrt{2\pi }}{{e}^{-\frac{{{({{\varepsilon }^{(i)}})}^{2}}}{2{{\sigma }^{2}}}}} p(ε(i))=σ2π1e−2σ2(ε(i))2
p ( y ( i ) ∣ x ( i ) , θ ) = 1 σ 2 π exp ( − ( ε ( i ) ) 2 2 σ 2 ) p({{y}^{(i)}}|{{x}^{(i)}},\theta )=\frac{1}{\sigma \sqrt{2\pi }}\exp (-\frac{{{({{\varepsilon }^{(i)}})}^{2}}}{2{{\sigma }^{2}}}) p(y(i)∣x(i),θ)=σ2π1exp(−2σ2(ε(i))2)
L ( θ ) = ∏ i = 1 m p ( y ( i ) ∣ x ( i ) , θ ) = ∏ i = 1 m 1 σ 2 π exp ( − ( ε ( i ) ) 2 2 σ 2 ) L(\theta )=\prod\limits_{i=1}^{m}{p({{y}^{(i)}}|{{x}^{(i)}},\theta )}=\prod\limits_{i=1}^{m}{\frac{1}{\sigma \sqrt{2\pi }}\exp (-\frac{{{({{\varepsilon }^{(i)}})}^{2}}}{2{{\sigma }^{2}}})} L(θ)=i=1∏mp(y(i)∣x(i),θ)=i=1∏mσ2π1exp(−2σ2(ε(i))2) - 对数似然、目标函数及最小二乘
l ( θ ) = ln L ( θ ) = ln ∏ i = 1 m 1 σ 2 π exp ( − ( ε ( i ) ) 2 2 σ 2 ) = ∑ i = 1 m ln ( 1 σ 2 π exp ( − ( ε ( i ) ) 2 2 σ 2 ) ) = m ln 1 σ 2 π − ∑ i = 1 m ( y ( i ) − θ T x ) 2 2 σ 2 l(\theta )=\ln L(\theta )=\ln \prod\limits_{i=1}^{m}{\frac{1}{\sigma \sqrt{2\pi }}\exp (-\frac{{{({{\varepsilon }^{(i)}})}^{2}}}{2{{\sigma }^{2}}})}=\sum\limits_{i=1}^{m}{\ln (\frac{1}{\sigma \sqrt{2\pi }}\exp (-\frac{{{({{\varepsilon }^{(i)}})}^{2}}}{2{{\sigma }^{2}}}))}=m\ln \frac{1}{\sigma \sqrt{2\pi }}-\frac{\sum\limits_{i=1}^{m}{{{({{y}^{(i)}}-{{\theta }^{T}}x)}^{2}}}}{2{{\sigma }^{2}}} l(θ)=lnL(θ)=lni=1∏mσ2π1exp(−2σ2(ε(i))2)=i=1∑mln(σ2π1exp(−2σ2(ε(i))2))=mlnσ2π1−2σ2i=1∑m(y(i)−θTx)2
l o s s ( y j , y ^ j ) = J ( θ ) = 1 2 ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) 2 loss({{y}_{j}},{{{\hat{y}}}_{j}})=J(\theta )=\frac{1}{2}\sum\limits_{i=1}^{n}{{{({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}})}^{2}}} loss(yj,y^j)=J(θ)=21i=1∑n(hθ(x(i))−y(i))2 - θ的求解过程
∇ θ J ( θ ) = ∇ θ ( 1 2 ( X θ − Y ) T ( X θ − Y ) ) = ∇ θ ( 1 2 ( θ T X T − Y T ) ( X θ − Y ) ) {{\nabla }_{\theta }}J(\theta )={{\nabla }_{\theta }}(\frac{1}{2}{{(X\theta -Y)}^{T}}(X\theta -Y))={{\nabla }_{\theta }}(\frac{1}{2}({{\theta }^{T}}{{X}^{T}}-{{Y}^{T}})(X\theta -Y)) ∇θJ(θ)=∇θ(21(Xθ−Y)T(Xθ−Y))=∇θ(21(θTXT−YT)(Xθ−Y))
∇ θ J ( θ ) = ∇ θ ( 1 2 ( θ T X T X θ − Y T X θ − θ T X T Y + Y T Y ) ) = 1 2 ( 2 X T X θ − X T Y − ( Y T X ) T ) {{\nabla }_{\theta }}J(\theta )={{\nabla }_{\theta }}(\frac{1}{2}({{\theta }^{T}}{{X}^{T}}X\theta -{{Y}^{T}}X\theta -{{\theta }^{T}}{{X}^{T}}Y+{{Y}^{T}}Y))=\frac{1}{2}(2{{X}^{T}}X\theta -{{X}^{T}}Y-{{({{Y}^{T}}X)}^{T}}) ∇θJ(θ)=∇θ(21(θTXTXθ−YTXθ−θTXTY+YTY))=21(2XTXθ−XTY−(YTX)T)
∇ θ J ( θ ) = X T X θ − X T Y = 0 {{\nabla }_{\theta }}J(\theta )={{X}^{T}}X\theta -{{X}^{T}}Y=0 ∇θJ(θ)=XTXθ−XTY=0
θ = ( X T X ) − 1 X T Y \theta ={{({{X}^{T}}X)}^{-1}}{{X}^{T}}Y θ=(XTX)−1XTY
1.2.2 最小二乘法的参数最优解
使得损失函数最小化的过程,成为线性回归模型的最小二乘“参数估计”(parameter estimation),从而得到最优解的闭式解,对于更一般的情形(样本由多个属性描述),称为“多元线性回归”(multivariate linear regression
参数解析式:
θ = ( X T X ) − 1 X T Y \theta ={{({{X}^{T}}X)}^{-1}}{{X}^{T}}Y θ=(XTX)−1XTY
最小二乘法的使用要求矩阵 ( X T X ) − 1 {{({{X}^{T}}X)}^{-1}} (XTX)−1 是可逆的(实际上是半正定矩阵);为了防止不可逆或者过拟合的问题存在,可以增加额外数据影响,导致最终的矩阵是可逆的:
θ = ( X T X + λ I ) − 1 X T Y \theta ={{({{X}^{T}}X\text{+}\lambda I)}^{-1}}{{X}^{T}}Y θ=(XTX+λI)−1XTY
最小二乘法直接求解的难点:矩阵逆的求解是一个难处np.linalg.inv()、matrix.I
1.2.3 最小二乘法的算例
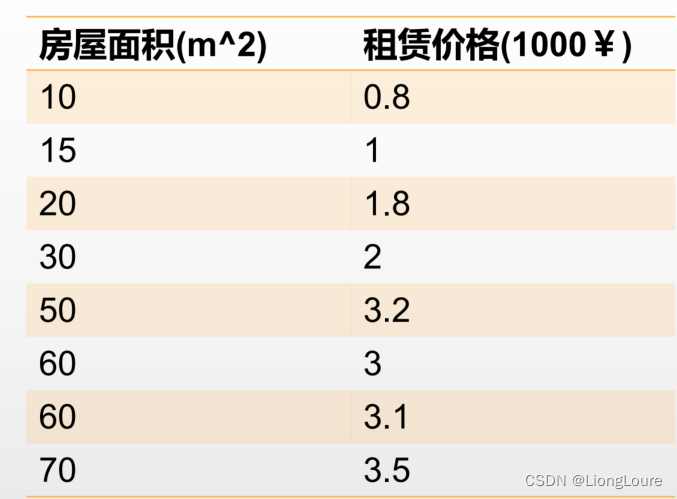
房价的预测
请问,如果现在有一个房屋面积为55平,请问最终的租赁价格是多少比 较合适?
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn.metrice import mean_squared_error.mean_absolutr_error,r2_score
import sys## 设置字符集,防止中文乱码
mpl.rcParams['font.sans-serif'] = [u'simHei']
mpl.rcParams['axes.unicode_minus'] = False
# 一、构造数据
X1 = np.array([10, 15, 20, 30, 50, 60, 60, 70]).reshape((-1, 1))
Y = np.array([0.8, 1.0, 1.8, 2.0, 3.2, 3.0, 3.1, 3.5]).reshape((-1, 1))# 添加一个截距项对应的X值 np.column_stack()
# X = np.hstack((np.ones_like(X1), X1))
X = np.column_stack((np.ones_like(X1), X1)) # 训练集fit
# 不加入截距项
# X = X1
# print(X)
# print(Y)
# sys.exit()
# 二、为了求解比较方便,将numpy的'numpy.ndarray'的数据类型转换为矩阵的形式的。
X = np.mat(X)
Y = np.mat(Y)# 三、根据解析式的公式求解theta的值
theta = (X.T * X).I * X.T * Y
print(theta)
# sys.exit()
# 四、 根据求解出来的theta求出预测值
predict_y = X * theta # 训练集的预测值
x_test = [[1, 55]] # 预测集
y_test_hat = x_test * theta # 预测值
print("价格:", y_test_hat)
# 查看MSE与R^2
print(Y.shape)
print(predict_y.shape)
mse = mean_squared_error(y_true=Y,y_pred=predict_y)
print('MSE',mse)
r2 = r2_score(y_true=Y,y_pred=predict_y)
print('r^2',r2)# print(predict_y)
# 五、画图可视化
plt.plot(X1, Y, 'bo', label=u'真实值')
plt.plot(X1, predict_y, 'r--o', label=u'预测值')
plt.plot(x_test[0][1], y_test_hat, 'b*')
plt.legend(loc='lower right')
plt.show()# 基于训练好的模型参数对一个未知的样本做一个预测
x = np.mat(np.array([[1.0, 55.0]]))
pred_y = x * theta
print("当面积为55平的时候,预测价格为:{}".format(pred_y))##TODO: 两个特征的时候的预测 【房屋面积55,房间数量2】时的预测结果 注意画图画3D图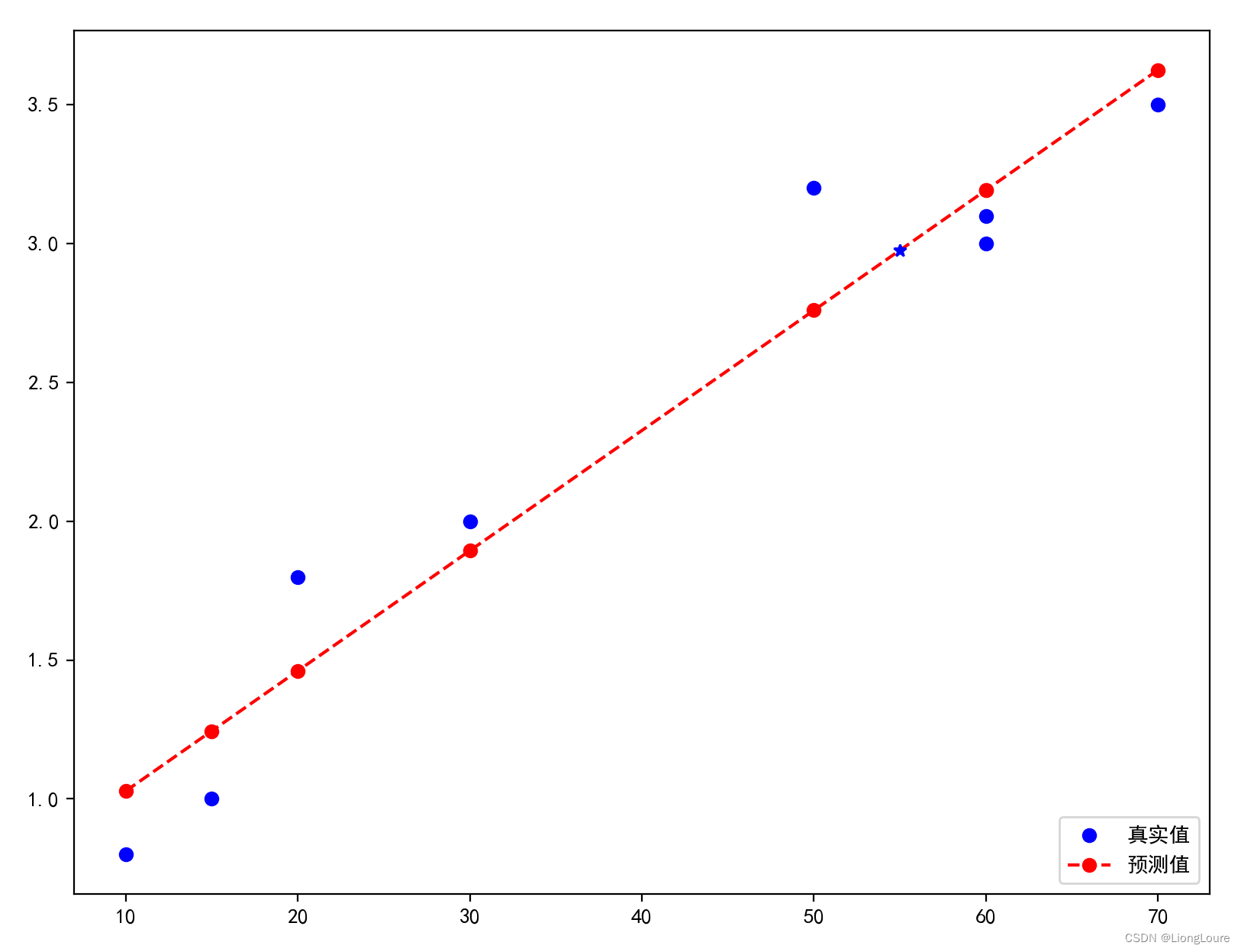
当面积为55平并且房间数目为2的时候,预测价格为:
# -- encoding:utf-8 --
"""
Create on 19/3/2
"""import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl## 设置字符集,防止中文乱码
mpl.rcParams['font.sans-serif'] = [u'simHei']
mpl.rcParams['axes.unicode_minus'] = Falseflag = True
# 一、构造数据
X1 = np.array([[10, 1],[15, 1],[20, 1],[30, 1],[50, 2],[60, 1],[60, 2],[70, 2]]).reshape((-1, 2))
Y = np.array([0.8, 1.0, 1.8, 2.0, 3.2, 3.0, 3.1, 3.5]).reshape((-1, 1))if flag:# 添加一个截距项对应的X值X = np.column_stack((X1, np.ones(shape=(X1.shape[0], 1))))# X = np.hstack((X1,np.ones(shape=(X1.shape[0], 1))))
else:# 不加入截距项X = X1
print(X)
# print(Y)# 二、为了求解比较方便,将numpy的'numpy.ndarray'的数据类型转换为矩阵的形式的。
X = np.mat(X)
Y = np.mat(Y)# 三、根据解析式的公式求解theta的值
theta = (X.T * X).I * X.T * Y
print(theta)# 四、 根据求解出来的theta求出预测值
predict_y = X * theta
# print(predict_y)
# 基于训练好的模型参数对一个未知的样本做一个预测
if flag:x = np.mat(np.array([[55.0, 2.0,1.0]]))
else:x = np.mat(np.array([[55.0, 2.0]]))
pred_y = x * theta
print("当面积为55平并且房间数目为2的时候,预测价格为:{}".format(pred_y))# 四、画图可视化(TODO: 自己更改为立体的图像)
from mpl_toolkits.mplot3d import Axes3Dx1 = X[:, 0]
print(x1)
x2 = X[:, 1]
print(x2)
fig = plt.figure(facecolor='w')
ax = Axes3D(fig)
ax.scatter(x1, x2, Y, s=40, c='r', depthshade=False) ###画点图x1 = np.arange(0, 100)
x2 = np.arange(0, 4)
x1, x2 = np.meshgrid(x1, x2)
# print(x1)
def predict(x1, x2, theta, base=False):if base:y_ = x1 * theta[0] + x2 * theta[1] + theta[2]else:y_ = x1 * theta[0] + x2 * theta[1]return y_
z = np.array(list(map(lambda t: predict(t[0], t[1], theta, base=flag), zip(x1.flatten(), x2.flatten()))))
z.shape = x1.shape
print(z.shape)
ax.plot_surface(x1, x2, z, rstride=1, cstride=1, cmap=plt.cm.jet) ##画超平面 cmap=plt.cm.jet彩图
ax.scatter(55,2, pred_y,c='b' )
ax.set_title(u'房屋租赁价格预测')
plt.show()
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl## 设置字符集,防止中文乱码
mpl.rcParams['font.sans-serif'] = [u'simHei']
mpl.rcParams['axes.unicode_minus'] = Falseflag = True
# 一、构造数据
X1 = np.array([[10, 1],[15, 1],[20, 1],[30, 1],[50, 2],[60, 1],[60, 2],[70, 2]]).reshape((-1, 2))
Y = np.array([0.8, 1.0, 1.8, 2.0, 3.2, 3.0, 3.1, 3.5]).reshape((-1, 1))if flag:# 添加一个截距项对应的X值X = np.column_stack((X1, np.ones(shape=(X1.shape[0], 1))))# X = np.hstack((X1,np.ones(shape=(X1.shape[0], 1))))
else:# 不加入截距项X = X1
print(X)
# print(Y)# 二、为了求解比较方便,将numpy的'numpy.ndarray'的数据类型转换为矩阵的形式的。
X = np.mat(X)
Y = np.mat(Y)# 三、根据解析式的公式求解theta的值
theta = (X.T * X).I * X.T * Y
print(theta)# 四、 根据求解出来的theta求出预测值
predict_y = X * theta
# print(predict_y)
# 基于训练好的模型参数对一个未知的样本做一个预测
if flag:x = np.mat(np.array([[55.0, 2.0,1.0]]))
else:x = np.mat(np.array([[55.0, 2.0]]))
pred_y = x * theta
print("当面积为55平并且房间数目为2的时候,预测价格为:{}".format(pred_y))# 四、画图可视化(TODO: 自己更改为立体的图像)
from mpl_toolkits.mplot3d import Axes3Dx1 = X[:, 0]
print(x1)
x2 = X[:, 1]
print(x2)
fig = plt.figure(facecolor='w')
ax = Axes3D(fig)
ax.scatter(x1, x2, Y, s=40, c='r', depthshade=False) ###画点图x1 = np.arange(0, 100)
x2 = np.arange(0, 4)
x1, x2 = np.meshgrid(x1, x2)
# print(x1)
def predict(x1, x2, theta, base=False):if base:y_ = x1 * theta[0] + x2 * theta[1] + theta[2]else:y_ = x1 * theta[0] + x2 * theta[1]return y_
z = np.array(list(map(lambda t: predict(t[0], t[1], theta, base=flag), zip(x1.flatten(), x2.flatten()))))
z.shape = x1.shape
print(z.shape)
ax.plot_surface(x1, x2, z, rstride=1, cstride=1, cmap=plt.cm.jet) ##画超平面 cmap=plt.cm.jet彩图
ax.scatter(55,2, pred_y,c='b' )
ax.set_title(u'房屋租赁价格预测')
plt.show()
3d绘图要点:
"""
绘制3d图形
"""import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
# 定义figure
fig = plt.figure()
# 创建3d图形的两种方式
# 将figure变为3d
ax = Axes3D(fig)# 定义x, y
x = np.arange(-4, 4, 0.25)
y = np.arange(-4, 4, 0.25)# 生成网格数据
X, Y = np.meshgrid(x, y)# 计算每个点对的长度
R = np.sqrt(X ** 2 + Y ** 2)
# 计算Z轴的高度
Z = np.sin(R)# 绘制3D曲面
# rstride:行之间的跨度 cstride:列之间的跨度
# rcount:设置间隔个数,默认50个,ccount:列的间隔个数 不能与上面两个参数同时出现
# cmap是颜色映射表
# from matplotlib import cm
# ax.plot_surface(X, Y, Z, rstride = 1, cstride = 1, cmap = cm.coolwarm)
# cmap = "rainbow" 亦可
# 我的理解的 改变cmap参数可以控制三维曲面的颜色组合, 一般我们见到的三维曲面就是 rainbow 的
# 你也可以修改 rainbow 为 coolwarm, 验证我的结论
ax.plot_surface(X, Y, Z, rstride = 1, cstride = 1, cmap = plt.get_cmap('rainbow'))# 绘制从3D曲面到底部的投影,zdir 可选 'z'|'x'|'y'| 分别表示投影到z,x,y平面
# zdir = 'z', offset = -2 表示投影到z = -2上
ax.contour(X, Y, Z, zdir = 'z', offset = -2, cmap = plt.get_cmap('rainbow'))# 设置z轴的维度,x,y类似
ax.set_zlim(-2, 2)plt.show()
线性回归模型最优的时候是所有样本的预测值和实际值之间的差值最小化,由于预测值和实际值之间的差值存在正负性,所以要求平方后的值最小化。也就是可以得到如下的一个目标函数:
J ( θ ) = 1 2 ∑ i = 1 m ( ε ( i ) ) 2 = 1 2 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta )=\frac{1}{2}\sum\limits_{i=1}^{m}{{{({{\varepsilon }^{(i)}})}^{2}}}=\frac{1}{2}\sum\limits_{i=1}^{m}{{{({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}})}^{2}}} J(θ)=21i=1∑m(ε(i))2=21i=1∑m(hθ(x(i))−y(i))2
建立一个线性回归对象后 :regression = LinearRegression(),对已有数据进行拟合:model = regression.fit(features,target),查看拟合后的结果:
- 查看截距:
model.intercept_ - 显示特征权重:
model.coef_
1.3 目标函数(loss/cost function)
回归任务评估指标: R 2 {{R}^{2}} R2,MSE,MAE
分类任务评估指标:Acc,Recall,Precision,F1,AUC
0-1损失函数: J ( θ ) = { 1 Y ≠ f ( X ) 0 Y = f ( X ) J(\theta )\text{=}\left\{ \begin{matrix} 1\text{ }Y\ne f(X) \\ 0\text{ }Y=f(X) \\\end{matrix} \right. J(θ)={1 Y=f(X)0 Y=f(X)
感知器损失函数: J ( θ ) = { 1 ∣ Y − f ( X ) ∣ > t 0 ∣ Y − f ( X ) ∣ ≤ t J(\theta )\text{=}\left\{ \begin{matrix} 1\text{ }\left| Y-f(X) \right|>t \\ 0\text{ }\left| Y-f(X) \right|\le t \\\end{matrix} \right. J(θ)={1 ∣Y−f(X)∣>t0 ∣Y−f(X)∣≤t
平方和损失函数 : J ( θ ) = ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta )\text{=}\sum\limits_{i=1}^{m}{{{({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}})}^{2}}} J(θ)=i=1∑m(hθ(x(i))−y(i))2
绝对值损失函数 : J ( θ ) = ∑ i = 1 m ∣ h θ ( x ( i ) ) − y ( i ) ∣ J(\theta )\text{=}\sum\limits_{i=1}^{m}{\left| {{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}} \right|} J(θ)=i=1∑m∣ ∣hθ(x(i))−y(i)∣ ∣
对数损失函数: J ( θ ) = − ∑ i = 1 m ( y ( i ) log h θ ( x ( i ) ) ) J(\theta )\text{=}-\sum\limits_{i=1}^{m}{({{y}^{(i)}}\log {{h}_{\theta }}({{x}^{(i)}}))} J(θ)=−i=1∑m(y(i)loghθ(x(i)))(适用于分类任务)
1.4 模型

欠拟合:拟合效果很差,模型过于简单(简单模型容易发生欠拟合)
过拟合:训练集拟合效果很好,但模型过于复杂(复杂模型容易发生过拟合)
机器学习开发流程
1、数据加载
2、数据进行清洗
3、获取我们的数据的特征属性X和目标属性Y
4、数据分割【指的是把数据划分为训练集和测试集】
5、特征工程 正则化、标准化,文本的处理
6、构建模型
7、训练模型
8、模型效果的评估 (效果不好,返回第二步进行优化,达到要求)
9、模型保存/模型的持久化
也可以使用其他模型、模型融合、增加数据集等方式,处理模型的欠拟合。
1.4.1 多项式拓展——升维(欠拟合)
from sklearn.preprocessing import PolynomialFeatures
PolynomialFeatures 多项式扩展
degree=2,扩展的阶数(不能过大)
interaction_only=False,是否只保留交互项(影响不大)
include_bias=True,是否需要偏置项
对于欠拟合——使模型更加复杂
一阶: ( x 1 , x 2 ) : x 1 , x 2 ({{x}_{1}},{{x}_{2}}):{{x}_{1}},{{x}_{2}} (x1,x2):x1,x2
二阶: ( x 1 , x 2 ) : x 1 2 , x 2 2 , x 1 x 2 ({{x}_{1}},{{x}_{2}}):{{x}_{1}}^{2},{{x}_{2}}^{2},{{x}_{1}}{{x}_{2}} (x1,x2):x12,x22,x1x2
但阶数越高容易导致过拟合
多项式拓展后——其本质仍为线性回归
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 {{h}_{\theta }}(x)={{\theta }_{0}}+{{\theta }_{1}}{{x}_{1}}+{{\theta }_{2}}{{x}_{2}} hθ(x)=θ0+θ1x1+θ2x2
→ h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 1 2 + θ 4 x 1 x 2 + θ 5 x 2 2 \to {{h}_{\theta }}(x)={{\theta }_{0}}+{{\theta }_{1}}{{x}_{1}}+{{\theta }_{2}}{{x}_{2}}+{{\theta }_{3}}{{x}_{1}}^{2}+{{\theta }_{4}}{{x}_{1}}{{x}_{2}}+{{\theta }_{5}}{{x}_{2}}^{2} →hθ(x)=θ0+θ1x1+θ2x2+θ3x12+θ4x1x2+θ5x22
→ h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 + θ 4 x 4 + θ 5 x 5 \to {{h}_{\theta }}(x)={{\theta }_{0}}+{{\theta }_{1}}{{x}_{1}}+{{\theta }_{2}}{{x}_{2}}+{{\theta }_{3}}{{x}_{3}}+{{\theta }_{4}}{{x}_{4}}+{{\theta }_{5}}{{x}_{5}} →hθ(x)=θ0+θ1x1+θ2x2+θ3x3+θ4x4+θ5x5
1.4.2 线性回归的过拟合——提前停止
目标函数: J ( θ ) = 1 2 ∑ i = 1 m ( ε ( i ) ) 2 = 1 2 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta )=\frac{1}{2}\sum\limits_{i=1}^{m}{{{({{\varepsilon }^{(i)}})}^{2}}}=\frac{1}{2}\sum\limits_{i=1}^{m}{{{({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}})}^{2}}} J(θ)=21i=1∑m(ε(i))2=21i=1∑m(hθ(x(i))−y(i))2
为了防止数据过拟合,也就是的θ值在样本空间中不能过大,可以在目标函数之上增加一个平方和损失:
J ( θ ) = 1 2 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ i = 1 n θ j 2 J(\theta )=\frac{1}{2}\sum\limits_{i=1}^{m}{{{({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}})}^{2}}}+\lambda \sum\limits_{i=1}^{n}{{{\theta }_{j}}^{2}} J(θ)=21i=1∑m(hθ(x(i))−y(i))2+λi=1∑nθj2
正则项(norm)/惩罚项: λ ∑ i = 1 n θ j 2 \lambda \sum\limits_{i=1}^{n}{{{\theta }_{j}}^{2}} λi=1∑nθj2 这里这个正则项叫做L2-norm
L2-norm: J ( θ ) = 1 2 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ i = 1 n θ j 2 λ > 0 J(\theta )=\frac{1}{2}\sum\limits_{i=1}^{m}{{{({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}})}^{2}}}+\lambda \sum\limits_{i=1}^{n}{{{\theta }_{j}}^{2}}\text{ }\lambda >0 J(θ)=21i=1∑m(hθ(x(i))−y(i))2+λi=1∑nθj2 λ>0
L1-norm: J ( θ ) = 1 2 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ i = 1 n ∣ θ j ∣ λ > 0 J(\theta )=\frac{1}{2}\sum\limits_{i=1}^{m}{{{({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}})}^{2}}}+\lambda \sum\limits_{i=1}^{n}{\left| {{\theta }_{j}} \right|}\text{ }\lambda >0 J(θ)=21i=1∑m(hθ(x(i))−y(i))2+λi=1∑n∣θj∣ λ>0
正则化(regularization)是一种通过惩罚复杂模型来减小其方差的方法。准确的说,就是将一个罚项加在我们希望最小化的损失函数上,λ值取值越大,对越大的参数值(也就是更复杂的模型)的惩罚就越重。
1.4.3 Ridge回归
使用L2正则的线性回归模型就称为Ridge回归(岭回归):
J ( θ ) = 1 2 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ i = 1 n θ j 2 λ > 0 J(\theta )=\frac{1}{2}\sum\limits_{i=1}^{m}{{{({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}})}^{2}}}+\lambda \sum\limits_{i=1}^{n}{{{\theta }_{j}}^{2}}\text{ }\lambda >0 J(θ)=21i=1∑m(hθ(x(i))−y(i))2+λi=1∑nθj2 λ>0
此时,所求得的θ参数解析式为:
θ = ( X T X + λ I ) − 1 X T Y \theta ={{({{X}^{T}}X\text{+}\lambda I)}^{-1}}{{X}^{T}}Y θ=(XTX+λI)−1XTY
1.4.4 LASSO回归——特征选择
使用L1正则的线性回归模型就称为LASSO回归(Least Absolute Shrinkage and Selection Operator):
J ( θ ) = 1 2 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ i = 1 n ∣ θ j ∣ λ > 0 J(\theta )=\frac{1}{2}\sum\limits_{i=1}^{m}{{{({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}})}^{2}}}+\lambda \sum\limits_{i=1}^{n}{\left| {{\theta }_{j}} \right|}\text{ }\lambda >0 J(θ)=21i=1∑m(hθ(x(i))−y(i))2+λi=1∑n∣θj∣ λ>0
Ridge(L2-norm)和LASSO(L1-norm)比较:
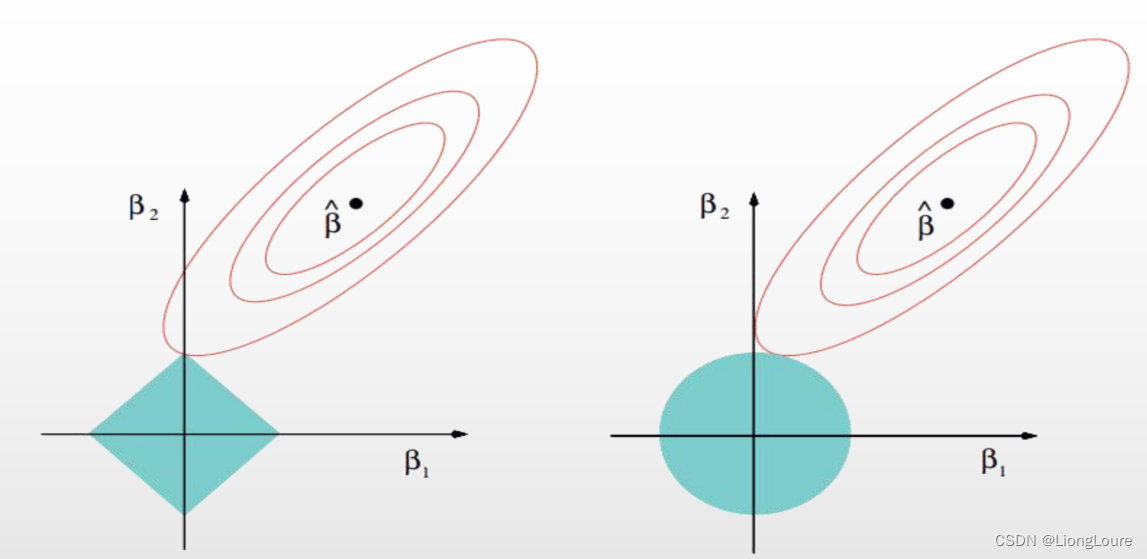
L2-norm中,由于对于各个维度的参数缩放是在一个圆内缩放的,不可能导致有维度参数变为0的情况,那么也就不会产生稀疏解;实际应用中,数据的维度中是存在噪音和冗余的,稀疏的解可以找到有用的维度并且减少冗余,提高后续算法预测的准确性和鲁棒性(减少了overfitting)(L1-norm可以达到最终解的稀疏性的要求)Ridge模型具有较高的准确性、鲁棒性以及稳定性(冗余特征已经被删除了);LASSO模型具有较高的求解速度——更容易在坐标轴上相切——相当于特征过滤,进行一次特征筛选。
上图中,β为参数空间,蓝色部分为约束区域 ∣ β 1 ∣ + ∣ β 2 ∣ ≤ t \left| {{\beta }_{1}} \right|+\left| {{\beta }_{2}} \right|\le t ∣β1∣+∣β2∣≤t(左——L1) ∣ β 1 ∣ 2 + ∣ β 2 ∣ 2 ≤ t 2 {{\left| {{\beta }_{1}} \right|}^{2}}+{{\left| {{\beta }_{2}} \right|}^{2}}\le {{t}^{2}} ∣β1∣2+∣β2∣2≤t2(右——L2),红色线条为最小二乘误差函数的等高投影线,t为约束范围(在拉格朗日乘子法中,将不等式约束问题转换为无约束条件问题——KKT,t并不重要)
如果既要考虑稳定性也考虑求解的速度,就使用Elasitc Net
1.4.5 Elasitc Net
同时使用L1正则和L2正则的线性回归模型就称为Elasitc Net算法(弹性网络算法)
J ( θ ) = 1 2 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ( p ∑ i = 1 n ∣ θ j ∣ +(1 − p ) ∑ i = 1 n θ j 2 ) J(\theta )=\frac{1}{2}\sum\limits_{i=1}^{m}{{{({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}})}^{2}}}+\lambda (p\sum\limits_{i=1}^{n}{\left| {{\theta }_{j}} \right|}\text{ +(1}-p\text{)}\sum\limits_{i=1}^{n}{{{\theta }_{j}}^{2}}) J(θ)=21i=1∑m(hθ(x(i))−y(i))2+λ(pi=1∑n∣θj∣ +(1−p)i=1∑nθj2)
1.5 模型效果判断
M S E = 1 m ∑ i = 1 m ( y i − y ^ i ) 2 MSE=\frac{1}{m}\sum\limits_{i=1}^{m}{{{({{y}_{i}}-{{{\hat{y}}}_{i}})}^{2}}} MSE=m1i=1∑m(yi−y^i)2
R M S E = M S E = 1 m ∑ i = 1 m ( y i − y ^ i ) 2 RMSE=\sqrt{MSE}=\sqrt{\frac{1}{m}\sum\limits_{i=1}^{m}{{{({{y}_{i}}-{{{\hat{y}}}_{i}})}^{2}}}} RMSE=MSE=m1i=1∑m(yi−y^i)2
R 2 = 1 − R S S T S S = 1 − ∑ i = 1 m ( y i − y ^ i ) 2 ∑ i = 1 m ( y i − y ˉ i ) 2 y ˉ i = 1 m ∑ i = 1 m y i {{R}^{2}}=1-\frac{RSS}{TSS}=1-\frac{\sum\limits_{i=1}^{m}{{{({{y}_{i}}-{{{\hat{y}}}_{i}})}^{2}}}}{\sum\limits_{i=1}^{m}{{{({{y}_{i}}-{{{\bar{y}}}_{i}})}^{2}}}}\text{ }{{{\bar{y}}}_{i}}=\frac{1}{m}\sum\limits_{i=1}^{m}{{{y}_{i}}} R2=1−TSSRSS=1−i=1∑m(yi−yˉi)2i=1∑m(yi−y^i)2 yˉi=m1i=1∑myi
R 2 ∈ ( − ∞ , 1 ) {{R}^{2}}\in (-\infty ,1) R2∈(−∞,1)
模型效果判断 :
MSE: 误差平方和,越趋近于0表示模型越拟合训练数据。
RMSE: MSE的平方根,作用同MSE
R2: 取值范围(负无穷,1],值越大表示模型越拟合训练数据;最优解是1;当模型预测为随机值的时候,有可能为负;若预测值恒为样本期望,R2为0
TSS: 总平方和TSS(Total Sum of Squares),表示样本之间的差异情况,是伪方差的m倍 T S S = ∑ i = 1 m ( y i − y ˉ i ) 2 TSS=\sum\limits_{i=1}^{m}{{{({{y}_{i}}-{{{\bar{y}}}_{i}})}^{2}}} TSS=i=1∑m(yi−yˉi)2
ESS: Explained Sum of Squares 回归平方和/解释平方和 ,被解释变量Y的估计值与其平均值的离差平方和(回归平方和) E S S = ∑ i = 1 m ( y ^ i − y ˉ i ) 2 ESS=\sum\limits_{i=1}^{m}{{{({{{\hat{y}}}_{i}}-{{{\bar{y}}}_{i}})}^{2}}} ESS=i=1∑m(y^i−yˉi)2
RSS: 残差平方和RSS(Residual Sum of Squares),表示预测值和样本值之间的差异情况,是MSE的m倍 T S S = ∑ i = 1 m ( y i − y ^ i ) 2 TSS=\sum\limits_{i=1}^{m}{{{({{y}_{i}}-{{{\hat{y}}}_{i}})}^{2}}} TSS=i=1∑m(yi−y^i)2
2. 代码实例
from sklearn.linear_model import LinearRegression
2.1 线性回归伪代码
import numpy as np
import joblibclass Linear:def __init__(self, b=True):self.b = b # 是否有截距; 判断依据: 是否过原点, 特征属性X全为0时, 目标值y是否也等于0self.theta0 = 0 # 截距θself.theta = None # θ参数矩阵def train(self, X, Y):# 如果有截距项, 那么需要插入全是1的X0列if self.b == True:X = np.column_stack((np.ones_like(X[:, 0]), X))# 二、为了求解比较方便,将numpy的'numpy.ndarray'的数据类型转换为矩阵的形式的。X = np.mat(X)Y = np.mat(Y)# 三、根据解析式的公式求解theta的值theta = (X.T * X).I * X.T * Yif self.b == True:self.theta0 = theta[0]self.theta = theta[1:]else:self.theta0 = 0self.theta = thetadef predict(self, X):# 首先判断模型是否存在if self.theta is None:print("Error: 模型不存在")returnX = np.mat(X)# y = x0 * 1 + x1 * w1 + x2 * w2predict_y = self.theta0 + X * self.thetareturn predict_ydef score(self, X, Y, type=1):"""type: 评估模型的类别, 0--MSE, 1--R^2, 2--MAE"""X = np.mat(X)Y = np.mat(Y)pred_y = self.predict(X) # 获取测试值# 输出不同的评估结果if type == 0:# MSEScoreNum = np.mean(np.sum(np.square(Y - pred_y)))elif type == 1:# R^2rss = np.sum(np.square(Y - pred_y))tss = np.sum(np.square(Y - np.mean(Y)))ScoreNum = 1 - rss / tsselif type == 2:# MAEScoreNum = np.mean(np.abs(Y - pred_y))else:print("Error: 请选择正确的评估模型!")returnreturn ScoreNumdef save(self, SavePath):# 首先判断模型是否存在if self.theta is None:print("Error: 模型不存在")return# 开始保存模型try:SaveTup = (self.theta0, self.theta) # 把两部分参数放进一个元组joblib.dump(SaveTup, SavePath)print("保存模型成功")except:print("Error: 保存模型错误!")def load(self, LoadPath):try:self.theta0, self.theta = joblib.load(LoadPath)print("加载模型成功")except:print("Error: 加载模型错误!")# 测试程序入口
if __name__ == "__main__":# X的训练数据in_x = np.array([[10, 1],[15, 1],[20, 1],[30, 1],[50, 2],[60, 1],[60, 2],[70, 2]])in_y = np.array([0.8, 1.0, 1.8, 2.0, 3.2, 3.0, 3.1, 3.5]).reshape(-1, 1)# 创建线性回归实例lg1 = Linear()# lg1.train(in_x, in_y)# # 显示得分# print(lg1.score(in_x,in_y))# 保存与加载path = r"D:\MyCourse\PythonFiles\MachineLearning\LinearRegression_my.m"# lg1.save(path) # 保存# 加载并测试lg1.load(path)print(lg1.score(in_x, in_y, 0))
2.2 波士顿房屋价格预测
2.2.1 原始数据——欠拟合
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import matplotlib as mpt# 加载数据
data = pd.read_csv('D:/datas/boston_housing.data', sep='\s+', header=None)# 数据预处理# 获取特征属性X和目标属性Y
X = data.iloc[:, :-1]
Y = data.iloc[:, -1]# 划分训练集和测试集
xTarin, xTest, yTarin, yTest = train_test_split(X, Y, test_size=0.3, random_state=10)# 构建模型
# fit_intercept是否需要截距项
linear = LinearRegression(fit_intercept=True) # 存在截距项# 模型训练
linear.fit(xTarin, yTarin)
print(linear.coef_) # 非截距项系数
print(linear.intercept_) # 截距项系数
yPredict = linear.predict(xTest)
print(linear.score(xTarin, yTarin)) # 默认为r^2
print(linear.score(xTest, yTest))
y_train_hat = linear.predict(xTarin)# 训练集
plt.plot(range(len(xTarin)), yTarin, 'r', label=u'true')
plt.plot(range(len(xTarin)), y_train_hat, 'g', label=u'predict')
plt.legend(loc='upper right')
plt.show()# 测试集
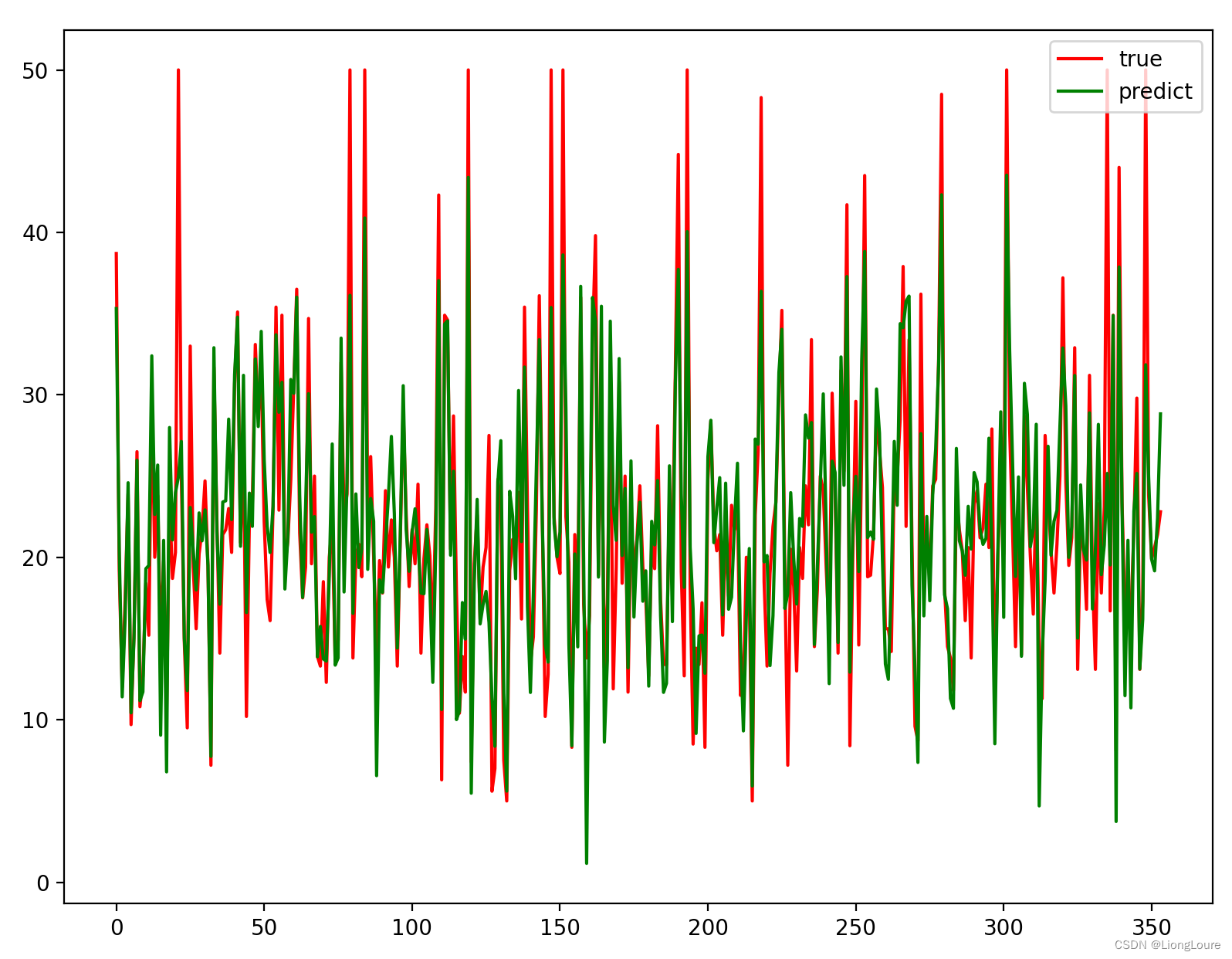
plt.plot(range(len(xTest)), yTest, 'r', label=u'true')
plt.plot(range(len(xTest)), yPredict, 'g', label=u'predict')
plt.legend(loc='upper right')
plt.show()
# todo:根据参数解析式写一个线性回归的伪代码,然后用波士顿房屋数据跟我们sklearn的库作比较

2.2.2 原始数据——多项式拓展(Linear)/ Ridge回归 / LASSO回归
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression, Lasso, Ridge, ElasticNet
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
import matplotlib.pyplot as plt
import matplotlib as mpt
import sys# 加载数据
data = pd.read_csv('d:/datas/boston_housing.data', sep='\s+', header=None)# 获取特征属性X和目标属性Y
X = data.iloc[:, :-1]
Y = data.iloc[:, -1]# 划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.3, random_state=10)# 特征工程
print(x_train.shape)
print(x_test.shape)
print(x_test.iloc[0,:])
poly = PolynomialFeatures(degree=2, interaction_only=True, include_bias=False)
'''
PolymomialFeatures # 多项式拓展
degree = 2 # 拓展的阶数
interaction_only=True # 是否只保留交互项(多项式拓展中的x1x2,x2x3,x1x3)
include_bias=False # 是否需要偏置项
''''''
fit 归一化,最大值/最小值等
fit_transform 针对训练数据使用
transform 特征转换
'''
x_train_poly = poly.fit_transform(x_train)
x_test_poly = poly.transform(x_test)
print(x_train_poly.shape)
print(x_test_poly.shape)
# print(x_test_poly[0])
# sys.exit()# 构建模型
linear = LinearRegression(fit_intercept=True)
# lasso = Lasso(alpha=1000, fit_intercept=True) # alpha越小,惩罚力度越小,更‘不容易’达到最优点。r2越大
# ridge = Ridge(alpha=1.0, fit_intercept=True)# 模型训练
linear.fit(x_train_poly, y_train)
# lasso.fit(x_train_poly, y_train)
# ridge.fit(x_train_poly, y_train)
print(linear.coef_)
print(linear.intercept_)
# print(lasso.coef_)
# print(lasso.intercept_)
# print(ridge.coef_)
# print(ridge.intercept_)# 预测测试机
y_test_hat = linear.predict(x_test_poly)
# y_test_hat = lasso.predict(x_test_poly)
# y_test_hat = ridge.predict(x_test_poly)
print("-" * 100)
print(linear.score(x_train_poly, y_train))
print(linear.score(x_test_poly, y_test))
# print(lasso.score(x_train_poly, y_train))
# print(lasso.score(x_test_poly, y_test))
# print(ridge.score(x_train_poly, y_train))
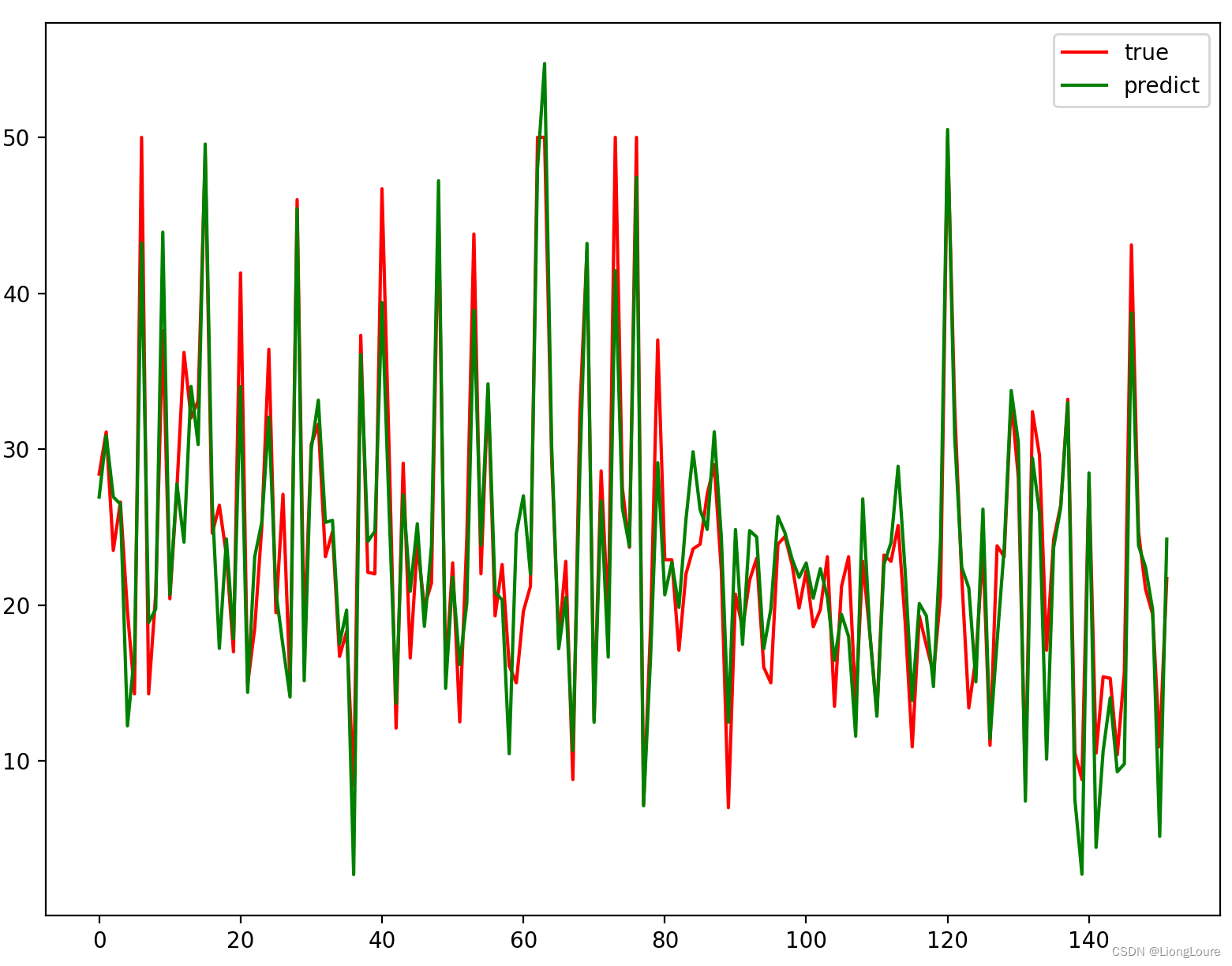
# print(ridge.score(x_test_poly, y_test))plt.plot(range(len(x_test)), y_test, 'r', label=u'true')
plt.plot(range(len(x_test)), y_test_hat, 'g', label=u'predict')
plt.legend(loc='upper right')
plt.show()# todo:根据参数解析式写一个线性回归的伪代码,然后用波士顿房屋数据跟我们sklearn的库作比较
2.2.3 忽略警告
import warnings
warnings.filterwarnings("ignore")
3. 机器学习调参
在实际工作中,对于各种算法模型(线性回归)来讲,我们需要获取θ、λ、p的值;
θ的求解其实就是算法模型的求解,一般不需要开发人员参与(算法已经实现),主要需要求解的是λ和p的值,这个过程就叫做调参(超参)
模型参数——实际上公式中求得的参数,不需要/不能手动调整,如线性回归中的θ。
超参数——需要人工调整设置的参数(调整):如KNN中的k值,多项式拓展中的degree
调参的目的——选择最优的参数——找到最优的函数映射关系:g——模型效果评估指标——交叉验证
交叉验证: 将训练数据分为多份,其中一份进行数据验证并获取最优的超参:λ和p;比如:十折交叉验证、五折交叉验证(scikit-learn中默认)等
五折交叉验证:
将数据分为5份,其中四份作为训练集,一份作为验证集,将所有情况下的验证集指标的平均值作为评估指标(每条数据都当做过验证集,更具有普适性,而单条数据的结果更具有随机性)——稳定性更强
4. 线性回归总结
算法模型: 线性回归(Linear)、岭回归(Ridge)、LASSO回归、Elastic Net
正则化: L1-norm、L2-norm ——过拟合
损失函数/目标函数: J ( θ ) = 1 2 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 → min θ J ( θ ) J(\theta )=\frac{1}{2}\sum\limits_{i=1}^{m}{{{({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}})}^{2}}}\to \underset{\theta }{\mathop{\min }}\,J(\theta ) J(θ)=21i=1∑m(hθ(x(i))−y(i))2→θminJ(θ)
θ求解方式: 最小二乘法(直接计算,目标函数是平方和损失函数)、梯度下降(BGD\SGD\MBGD)
这篇关于[深度学习]Part2(线性)回归算法Ch03——【DeepBlue学习笔记】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!