[异常检测]Memorizing Normality to Detect Anomaly: Memory-augmented Deep Autoencoder for Unsupervised

本文主要是介绍[异常检测]Memorizing Normality to Detect Anomaly: Memory-augmented Deep Autoencoder for Unsupervised，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

源码地址：https://github.com/donggong1/memae-anomaly-detection

问题提出

''It has been observed that sometimes the autoencoder “generalizes” so well that it can also reconstruct anomalies well, leading to the miss detection of anomalies ‘’

“The assumption that anomaly incurs higher reconstruction error might be somehow questionable since there are no training samples for anomalies and the reconstruction behavior for anomaly inputs should be unpredictable."

当前基于reconstruction error的方法，因为ae存在的泛化性能，导致anomaly data也可能具有较小的重构损失，检测效果较差。

问题解决

通过memory机制改善autoencoder

在训练过程中利用训练样本更新一个memory bank，该memory bank用来表示normal样本的prototype。测试过程中，memory bank固定，对某一个测试样本搜索一些prototypes并加权求和，代表该测试样本，并进行重构误差计算。（因为是利用normal prototype进行重构，因此对于异常样本，重构损失肯定会增加）

attention based memory addressing来寻找most relevant items in memory bank
hard shrinkage operator to induce sparsity of memory addressing weights

模型结构

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-80zIWhcX-1631793091790)(C:\Users\Administrator\AppData\Roaming\Typora\typora-user-images\image-20210916185940401.png)]$

encoder
$f_e : X \rightarrow Z \\ z = f_e(x;\theta_e)$
z既是x的表征，同时也作为query，在memory bank中搜索最相关的prototype
decoder
$\hat{x}=f_d(\hat{z};\theta_d)$
其中 $\hat{z}$ 是相关prototype经过加权求和所得的表征。
memory module

包含了memory bank用来存储prototype和一个attention-based addressing operator用来计算权重。

用 $\in R^{N \times C }$ 表示memory bank，也就是保留有N个prototypes，则
$\hat{z} = \sum_i^Nw_im_i$
其中权重由encode z经过attention获得：

利用memory item与query(z)的相似度求权重：
$w_i = \frac{exp(d(z,m_i))}{\sum_i^Nexp(d(z,m_j))}$
其中相似度度量是通过余弦相似度获得。

论文中提到这样的memory module带来的优势如下：

在训练阶段，模型限制retrieve的memory items尽可能少，以此来有效利用memory items，使得prototype最具有代表性

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xKo3RVCi-1631793091792)(C:\Users\Administrator\AppData\Roaming\Typora\typora-user-images\image-20210916192722800.png)]$

论文展示了模型中的prototype解码之后的图片，可以看到较能代表训练数据

在测试阶段，模型对normal样本可以正常reconstruct，但是对于异常样本，因为memory construct的表征 $\hat{z}$ 是正常数据的加权求和，因此重构得到的图片也会接近训练样本，导致重构误差较大。如下图，可以看到当输入一个异常样本，重构的图片在提出的模型下会很接近正常样本。

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RHUrIBB8-1631793091793)(C:\Users\Administrator\AppData\Roaming\Typora\typora-user-images\image-20210916193046517.png)]$
hard shrinkage for sparse addressing

文章中提到，如果对memory的权重没有限制的话，一个较复杂的加权和仍然可能使得异常样本重构误差较小，因此期望限制所利用的memory items，利用hard shrinkage operation来增加w的稀疏性。

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MyMTJH1v-1631793091794)(C:\Users\Administrator\AppData\Roaming\Typora\typora-user-images\image-20210916193938004.png)]$

这样的非连续操无法进行反向传播，因此考虑利用一个Relu激活函数：

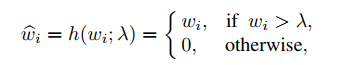
在这里插入图片描述

实际的操作将阈值设定为[1/N , 3/N]之间，再对操作后的权重进行归一化。

在训练过程中，除了这样一个hard shrinkage操作，论文还提出可以最小化 $\hat{w}_i$ 的熵，以此来提升其稀疏性。
$E(\hat{w}) = \sum_i^T-\hat{w_i}log(\hat{w_i})$
整体损失函数如下，前一部分为重构损失（L2范数）
$\frac{1}{T}\sum_t^T(R(x,\hat{x})+\alpha E(\hat{w}))$

实验部分

论文的实验对图像、视频以及文本类数据进行了大量的实验，实验结果如下：

图像

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7drcUZun-1631793091796)(C:\Users\Administrator\AppData\Roaming\Typora\typora-user-images\image-20210916194843613.png)]$
视频

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MTWJgi4y-1631793091796)(C:\Users\Administrator\AppData\Roaming\Typora\typora-user-images\image-20210916194922229.png)]$
文本(KDDCUP)

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JcscjCDT-1631793091797)(C:\Users\Administrator\AppData\Roaming\Typora\typora-user-images\image-20210916194957397.png)]$