协同过滤算法之连续评分通过皮尔逊相关系数计算相似度原理及代码实现

相关算法介绍

余弦相似度

• 度量的是两个向量之间的夹角, 用夹角的余弦值来度量相似的情况
• 两个向量的夹角为0是,余弦值为1, 当夹角为90度是余弦值为0,为180度是余弦值为-1
• 余弦相似度在度量文本相似度, 用户相似度 物品相似度的时候较为常用
• 余弦相似度的特点, 与向量长度无关,余弦相似度计算要对向量长度归一化, 两个向量只要方向一致,无论程度强弱, 都可以视为’相似’
  

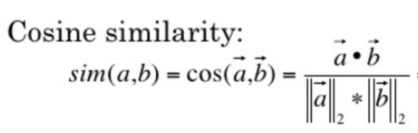
皮尔逊（Pearson）相关系数

• 实际上也是一种余弦相似度, 不过先对向量做了中心化, 向量a b 各自减去向量的均值后, 再计算余弦相似度
• 皮尔逊相似度计算结果在-1,1之间 -1表示负相关, 1表示正相关
• 度量两个变量是不是同增同减
• 皮尔逊相关系数度量的是两个变量的变化趋势是否一致, 不适合计算布尔值向量之间的相关度
  

使用协同过滤推荐算法对用户进行评分预测

协同过滤推荐算法数据集

• 在上次通过Jaccard相似度计算，我们只是创建了用户对物品的一个购买记录，也可以是浏览点击记录、收听记录等等。这样数据我们预测的结果主要是预测用户是否对某物品感兴趣，对于这件物品的喜好程度却不能很好的预测。

• 因此在协同过滤推荐算法中其实会更多的利用用户对某种物品的“评分”数据来进行预测，通过评分数据集，我们可以预测用户对于他没有评分过的物品进行评分。实现原理和思想和都是一样的，只是使用的数据集是用户-物品的评分数据。

关于用户-物品评分矩阵

• 用户-物品的评分矩阵，根据评分矩阵的稀疏程度会有不同的解决方案，一般有两种情形：

1. 稠密评分矩阵
   

2. 稀疏评分矩阵
   

代码及实现

• 构建数据集

import pandas as pd
import numpy as npusers = ["Thomas", "Cauchy", "Alice", "Bob", "Alex"]
items = ["iPad", "MacBook", "iPhone", "iWatch", "AirPods"]
#用户购买记录数据集
#构建评分数据时，对于缺失的部分我们需要保留为None，如果设置为0那么会被当作评分值为0去对待
datasets = [[5,3,4,4,None],[3,1,2,3,3],[4,3,4,3,5],[3,3,1,5,4],[1,5,5,2,1],
]

• 计算相似度

#对于评分数据这里我们采用皮尔逊相关系数[-1,1]来计算，-1表示强负相关，+1表示强正相关。 pandas中corr方法可直接用于计算皮尔逊相关系数
df = pd.DataFrame(datasets,columns=items,index=users)print("用户之间的两两相似度：")# 默认是按列进行计算，因此如果计算用户间的相似度，当前需要进行转置
user_similar = df.T.corr()
print(user_similar.round(4))print("物品之间的两两相似度：")
item_similar = df.corr()
print(item_similar.round(4))

Tips：我们在做预测评分时，往往是通过与其有正相关的用户或物品进行预测，如果不存在正相关的情况，那么将无法做出预测。在稀疏矩阵中尤为常见，因为稀疏评分矩阵中很难得出正相关系数。

如何计算评分预测？

1. User-Based CF 评分预测：使用用户间的相似度进行预测
   用户本身的评分评分以及近邻用户的加权平均相似度打分来进行预测
   
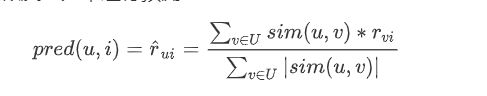
   我们要预测Thomas对AirPods的评分，那么可以根据与Thomas最近邻的Cauchy和Alice进行预测，计算如下：
   
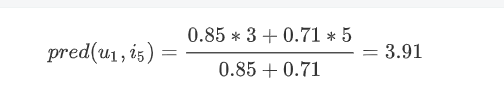
2. Item-Based CF 评分预测：使用物品间的相似度进行预测
   结合预测物品与相似物品的加权平均相似度打分进行来进行预测
   
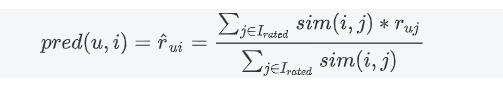
   我们要预测Thomas对AirPods的评分，那么可以根据与AirPods最近邻的iPad和iWatch进行预测，计算如下：
   

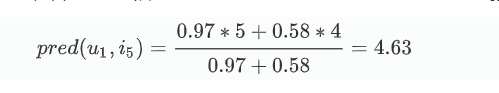
总结

User-Based CF预测评分和Item-Based CF的评分结果会存在差异，主要原因是他们其实是属于两种不同的推荐算法，各自在不同的领域与不同场景下，都会比另一种的效果更佳。如果是哪种是最佳评分，必须进行合理的效果评估，因此在实现推荐系统时这两种算法往往都是需要去实现的，然后对产生的推荐效果进行评估分析选出更优方案。