本文主要是介绍DOA估计算法——迭代自适应算法(IAA),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1 简介
迭代自适应法 (Iterative Adaptive Approach,IAA)估计算法最早由美国的电气工程师和数学家Robert Schmidt和Roy A. Kuc在1986年的一篇论文"Multiple Emitter Location and Signal Parameter Estimation"中首次提出了这一算法, IAA DOA 估计算法是一种用于无线通信和雷达系统中估计信号到达方向的方法,对于信号处理和通信领域具有重要意义。
对于实际的雷达DOA估计来说,传统的延时相加方法(Delay-And-Sum, DAS)分辨率低,旁瓣干扰大。而ESPRIT2I和MUSIC等方法只有在传感器数大于源信号数,并且需要大量的快拍数,和高信噪比的情况下来获得高分辨率,但是在实际的工程应用中,收集大量的快拍是不切实际的,尤其是在快速的时变环境很难做到这一点,使得定位性能恶化。此外,由于对子空间正交性比较敏感,基于子空间的方法也不能处理相干源问题。
IAA是一种依赖数据,基于加权最小二乘方法(WLS)的非参数的迭代自适应算法,它可以在少量快拍(甚至是一个)、相干或非相千源、任意阵列的情况下得到很好的参数估计,相比于其他依赖于数据的方法,IAA可以大大地增加分辨率并且减小旁瓣,所以它的性能要比现有的空间稀疏信号重构算法好。
阵列信号经常遇到的问题是少量的快拍数和低信噪比。针对这个问题应用IAA算法就可以很好地减小这些不利因素对信号估计的影响。由于实际信号往往要比观测信号少得多,所以,将阵列信号处理问题转换到稀疏信号表示领域。因为稀疏信号表示方法可以处理少量快拍数的情况,甚至是一个。而这种基于稀疏表示的方法也被用在频谱估计、图像处理、阵列设计和其他很多领域。
2 IAA算法原理
假设远场有K个窄带信号入射到有M个天线阵元的均匀阵列上,第k个信号的入射角度为![]() 。n时刻阵列接受的数据矢量可以表示为
。n时刻阵列接受的数据矢量可以表示为
![]()
式中N是快拍数量。![]() 是M×K的阵列流行矩阵,
是M×K的阵列流行矩阵,![]() ,n=1,2,…,N,是信号矩阵,e(n)表示加性噪声矩阵。A(θ)对于不同的阵列结构略有不同,对于均匀阵列第k个源一致的方向矢量可以表示为:
,n=1,2,…,N,是信号矩阵,e(n)表示加性噪声矩阵。A(θ)对于不同的阵列结构略有不同,对于均匀阵列第k个源一致的方向矢量可以表示为:
![]()
式中![]() 表示阵元间距,λ表示传播信号的波长。均匀线阵的结构如图1所示
表示阵元间距,λ表示传播信号的波长。均匀线阵的结构如图1所示

设P是一个K×K的对角矩阵,对角元素是扫描网格上每一个角度的信号能量,干扰和噪声的协方差矩阵为
![]()
其中![]() ,左式表示信号的协方差矩阵,右式表示协方差矩阵的特征分解形式。因此式(3)可以理解为出去有用信号剩余的量即为干扰和噪声。对于信号的协方差估计,通常可通过下式进行估计
,左式表示信号的协方差矩阵,右式表示协方差矩阵的特征分解形式。因此式(3)可以理解为出去有用信号剩余的量即为干扰和噪声。对于信号的协方差估计,通常可通过下式进行估计
![]()
IAA算法通过求解如下加权最小二乘代价函数:
![]()
式中![]() 表示第n次快拍θk处信号的复幅值。要精确得到估计结果,既要使得:
表示第n次快拍θk处信号的复幅值。要精确得到估计结果,既要使得:
![]()
达到最小,此时的![]() 成为最小二乘加权量,W即为加权矩阵。当W=I时,为非加权最小二乘估计。将式(6)对
成为最小二乘加权量,W即为加权矩阵。当W=I时,为非加权最小二乘估计。将式(6)对![]() 求偏导数,并令偏导数等于零,则得最小二乘的估计量
求偏导数,并令偏导数等于零,则得最小二乘的估计量
![]()
则估计的均方误差为:
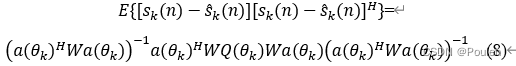
其中![]() 和
和![]() 是已知的,当
是已知的,当![]() 时,可以证明加权最小二乘法估计的均方误差是所有加权矩阵下最小的。这时可获得最佳加权最小二乘估计量为:
时,可以证明加权最小二乘法估计的均方误差是所有加权矩阵下最小的。这时可获得最佳加权最小二乘估计量为:
![]()
最终根据矩阵求逆定理可得:
![]()
最终,综上所述,IAA算法总结为:
Step1:初始化
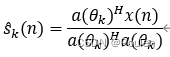
Step2:划分包含K个目标的离散网格
Step3:迭代
(1)计算![]()
(2)计算协方差矩阵![]()
(3) 更新![]() 。
。
(4)判断收敛,不收敛则回到(2),否则结束迭代。
3 IAA仿真
仿真环境:Matalb2021b,Windows11
阵元数量:M=16
目标来波方向:40°,10°,20°的非相干信号源
信号的中心频率为:f = 77GHz,信号能量幅度默认为1。
信噪比:SNR=5dB、16dB、30dB
收敛误差:小于![]()
快拍数:N = 1
仿真结果:
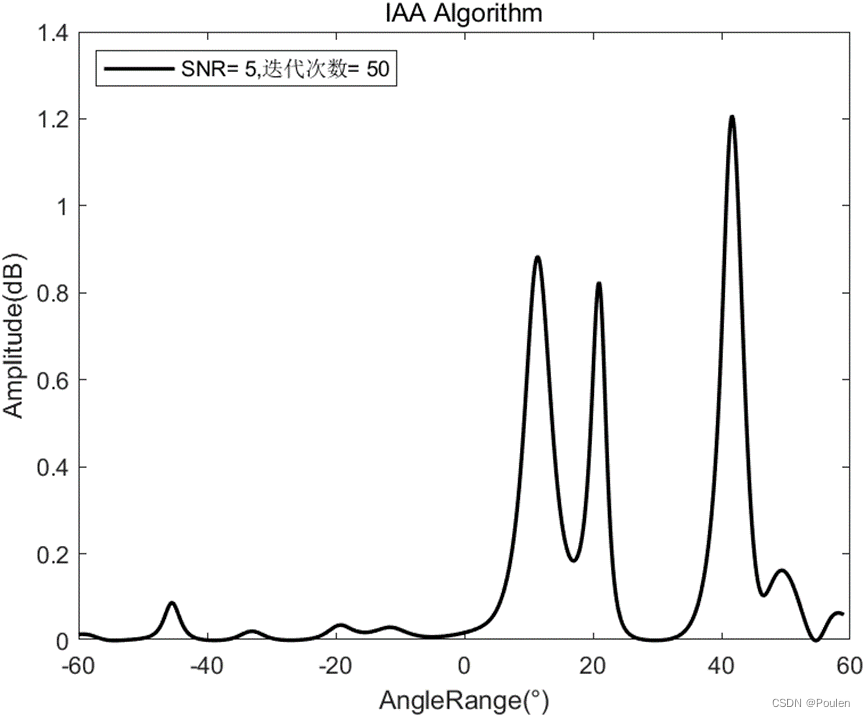
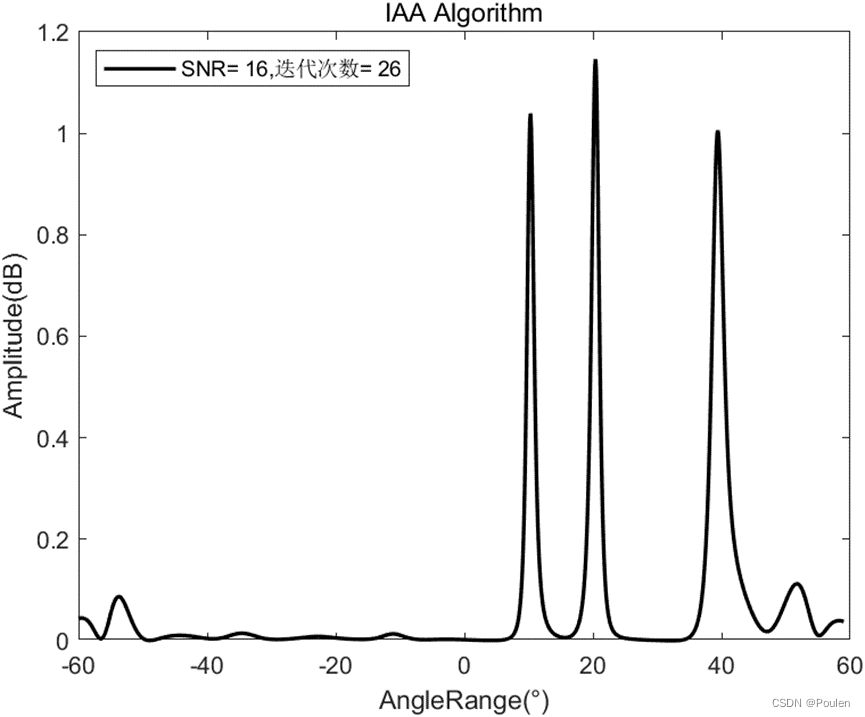
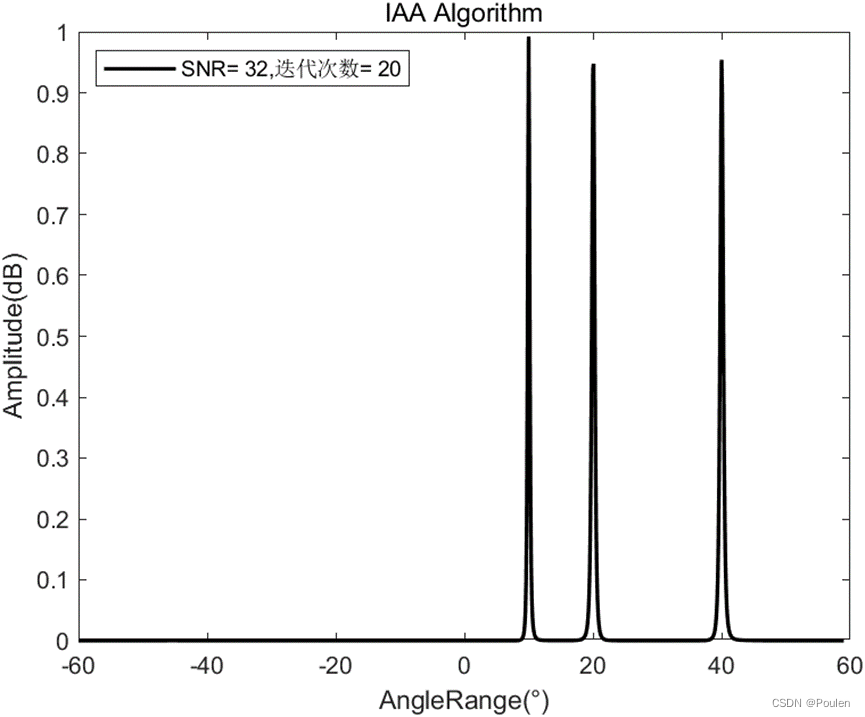
根据上述仿真结果,我们可以得出,随着信噪比的增大,要到达![]() 量级的误差,迭代次数显著减少,同时估计的精度也显著提高,目标旁瓣也显著降低。
量级的误差,迭代次数显著减少,同时估计的精度也显著提高,目标旁瓣也显著降低。
4 结束语
本期内容分析仿真了一种基于最小加权二乘法的IAA算法,通过选取合理的加权系数,更新协方差矩阵进行迭代计算,在低信噪比、单个快拍密集谱的情况下得到了非常精确的DOA和信号能量估计。阵列信号经常遇到的问题是少量的快拍数和低信噪比。针对这个问题应用IAA算法就可以很好地减小这些不利因素对信号估计的影响。此外希望本期内容对你有所帮助,另外创作不易,感谢支持。
5 参考资料
(eWiley) Optimum Array Processing. Harry L. Van Trees
基于迭代自适应方法的空间信号估计.
这篇关于DOA估计算法——迭代自适应算法(IAA)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








