本文主要是介绍信号系统之卷积性质,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1 常见的脉冲响应
最简单的脉冲响应是一个δ函数,如图7-1所示。也就是说,输入上的脉冲在输出上产生相同的脉冲。这意味着所有信号都毫无变化地通过系统。将任何信号与 δ函数进行卷积都会产生完全相同的信号。从数学上来说,可以这样写:

这个属性使得 δ函数成为卷积的恒等式。这类似于 0 是加法的恒等式 (a + 0 = a),1 是乘法的恒等式 (a×1 = a)。此类系统是数据存储、通信和测量的理想选择。 DSP 的大部分内容都涉及在系统中传递信息而不发生改变或降级。
图 7-1b 显示了对 δ函数脉冲响应的轻微修改。如果δ函数的幅度变大或变小,则所得系统分别是放大器或衰减器。以方程形式表示,如果 k 大于 1,则产生放大;如果 k 小于 1,则产生衰减:

图 7-1c 中的脉冲响应是带有偏移的 δ函数。这导致系统在输入和输出信号之间引入相同的偏移。这可以描述为信号延迟或信号提前,具体取决于移位的方向。让偏移由参数 s 表示,可以写成等式:
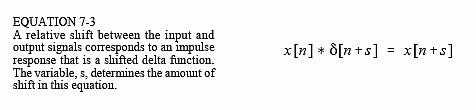
图 7-1d 显示了由 δ函数加上移位和缩放组成的脉冲响应。通过叠加,该系统的输出是输入信号加上输入信号的延迟版本,即回声。添加回声是使录音听起来自然悦耳的关键部分。雷达和声纳分析回波以检测飞机和潜艇。地球物理学家利用回波来寻找石油。

2 类似微积分的运算
卷积可以以类似于积分和微分的方式改变离散信号。由于术语 “导数”和“积分” 专门指对连续信号的运算,因此为它们的离散对应物赋予了其他名称。模拟一阶导数的离散运算称为一阶差分。同样,积分的离散形式称为运行和。
图 7-2 显示了实现一阶差分和运行总和的脉冲响应。

图 7-3 显示了使用这些操作的示例。在 7-3a 中,原始信号由具有不同斜率的多个部分组成,将该信号与一阶差分脉冲响应进行卷积,产生图 7-3b 中的信号。正如一阶导数一样,一阶差分信号中每个点的幅度等于原始信号中相应位置的斜率。运行和是一阶差分的逆运算。也就是说,将 (b) 中的信号与运行和的脉冲响应进行卷积,产生 (a) 中的信号。

这些脉冲响应非常简单,通常不需要完整的卷积程序来实现它们。相反,以另一种模式来考虑它们:输出信号中的每个样本都是来自输入的加权样本的总和。例如,可以计算第一个差值:

也就是说,输出信号中的每个样本等于输入信号中两个相邻样本之间的差,例如 y[40] = x[40] - x[39]。应该提到的是,这不是定义离散导数的唯一方法。另一种常见的方法是围绕所检查的点对称地定义斜率,例如:y[n] = (x[n+1] - x[n-1])/2。
使用相同的方法,可以通过对原始信号中样本位置左侧的所有点求和来计算运行总和中的每个样本。例如,如果 y[n] 是 x[n] 的运行和,则通过将样本 x[0] 到 x[40] 相加来找到样本 y[40]。同样,样本 y[41] 是通过将样本 x[0] 到 x[41] 相加得出的。当然,以这种方式计算运行总和是非常低效的。例如,如果 y[40] 已经计算出来,则只需一次加法即可计算 y[41]:y[41] = x[41] + y[40]。以方程形式表示:

这种类型的关系称为递归方程或差分方程。这些关系与使用图 7-2 的脉冲响应进行卷积相同。表 7-1 提供了实现这些类似微积分运算的计算机程序。

3 低通和高通滤波器
图 7-4 显示了几种常见的低通滤波器内核。一般来说,低通滤波器核由一组相邻的正点组成。这导致输出信号中的每个样本都是输入信号中许多相邻点的加权平均值。这种平均可以平滑信号,从而消除高频分量。如 © 中的 sinc 函数所示,一些低通滤波器内核在尾部包含一些负值样本。

通过使滤波器内核变宽或变窄来改变滤波器的截止频率。如果低通滤波器在 DC(零频率)时的增益为 1,则脉冲响应中所有点的总和必须等于 1,如 (a) 和 © 所示,一些滤波器内核理论上会扩展到无穷大,而不会降至零值。在实际应用中,尾部会在一定数量的样本后被截断,从而可以用有限数量的点来表示。不然如何将其存储在计算机中呢?
图 7-5 显示了三种常见的高通滤波器内核,它们源自图 7-4 中相应的低通滤波器内核。这是滤波器设计中的常见策略:首先设计一个低通滤波器,然后将其转换为需要的高通、带通、带阻等。了解低通到高通的转换,请记住,δ 函数脉冲响应会传递整个信号,而低通脉冲响应仅会传递低频分量。通过叠加,由 δ 函数减去低通滤波器内核组成的滤波器内核将使减去低频分量的整个信号通过。高通滤波器诞生了!如图7-5所示,δ函数通常添加在对称中心,或者如果滤波器核不对称则采样零。高通滤波器在直流(零频率)下具有零增益,这是通过使滤波器内核中所有点的总和等于零来实现的。

4 因果信号和非因果信号
模仿现实世界的系统,它必须遵循与现实世界相同的因果关系原则。例如,输入信号中样本号为 8 的值只能影响输出信号中样本号为 8 或更大的值,以这种方式运行的系统被称为因果系统。当然,数字处理不一定必须以这种方式运行。由于输入和输出信号都是存储在计算机中的数字数组,因此任何输入信号值都可以影响任何输出信号值。
如图 7-6 中的示例所示,对于所有负编号样本,因果系统的脉冲响应必须具有零值。从卷积的输入侧来看这一点。为了成为因果关系,样本编号为 n 的输入信号中的脉冲必须仅影响输出信号中样本编号为 n 或更大的那些点。在常见用法中,术语“因果”适用于所有负编号样本的值为零的任何信号,无论它是否是脉冲响应。

5 零相位、线性相位和非线性相位
如图 7-7 所示,如果信号围绕样本号 0 具有左右对称性,则称该信号为零相位。如果信号具有左右对称性,但在非零点附近,则称该信号为线性相位。这意味着任何线性相位信号只需通过左移或右移就可以变成零相位信号。最后,如果信号不具有左右对称性,则该信号被称为非线性相位。

相位与对称性有什么关系? 答案就在于频谱。简而言之,任何信号的频谱都由两部分组成:幅度和相位。围绕零对称的信号的频谱具有零相位。同样,围绕某个非零点对称的信号的频谱具有直线相位,即线性相位。最后,不对称的信号的频谱具有不是直线的相位,即具有非线性相位。
6 交换律
卷积的交换律用数学形式表示:

换句话说,两个信号的卷积顺序没有区别;结果是相同的。如图7-8所示,这对于系统论来说有着奇怪的意义。在任何线性系统中,输入信号和系统的脉冲响应都可以交换,而不改变输出信号。

7 关联属性
是否可以对三个或更多信号进行卷积? 答案是肯定的,关联属性描述了如何:将两个信号进行卷积以产生中间信号,然后将中间信号与第三个信号进行卷积。关联属性规定卷积的顺序并不重要。作为一个等式:
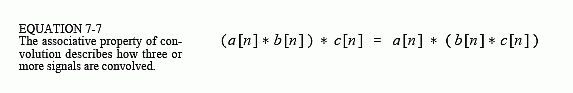
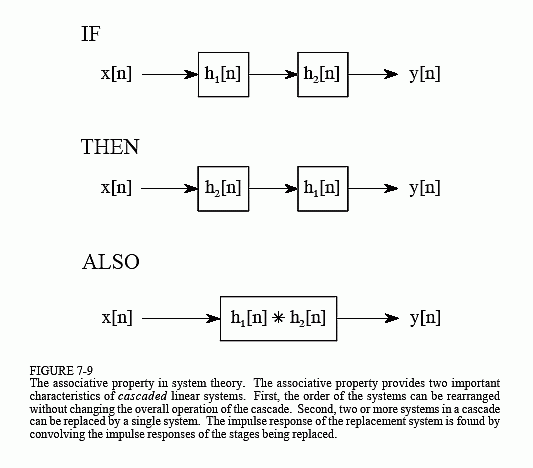
关联属性在系统理论中用于描述级联系统的行为方式。如图 7-9 所示,如果一个系统的输出用作下一个系统的输入,则称两个或多个系统处于级联状态。根据关联属性,可以重新排列系统的顺序,而不改变级联的整体响应。此外,任何数量的级联系统都可以用单个系统代替。通过对所有原始系统的脉冲响应进行卷积来找到替换系统的脉冲响应。
8 分配属性
分配律以方程形式写为:

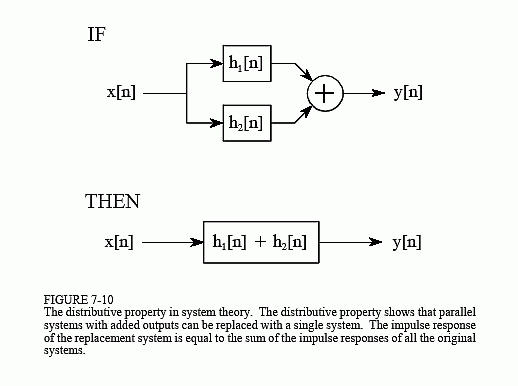
分布式属性描述了具有附加输出的并行系统的运行。如图 7-10 所示,两个或多个系统可以共享相同的输入 x[n],并将其输出相加以生成 y[n]。分布式特性允许用单个系统代替这种系统组合,该系统的脉冲响应等于原始系统的脉冲响应之和。
9 输入和输出之间的传输
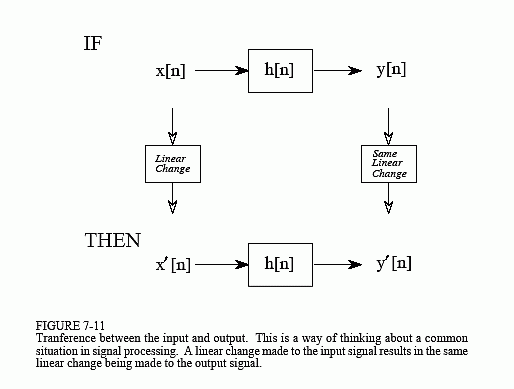
这不是一个正式的数学属性,而是一种思考信号处理中常见情况的方式。如图 7-11 所示,输出信号以与输入信号变化完全相同的线性方式变化。例如,如果输入信号被放大两倍,则输出信号也将被放大两倍。如果对输入信号求导,则也将对输出信号求导。如果以某种方式对输入进行过滤,则输出也将以相同的方式进行过滤。这可以通过使用关联属性轻松证明。
10 中心极限定理
中心极限定理是概率论中的一个重要工具,因为它从数学上解释了为什么在自然界中如此普遍地观察到高斯概率分布。其以最简单的形式指出,当观察到的变量是许多随机过程的总和时,就会产生高斯分布,即使组件过程不具有高斯分布,它们的总和也会具有高斯分布。
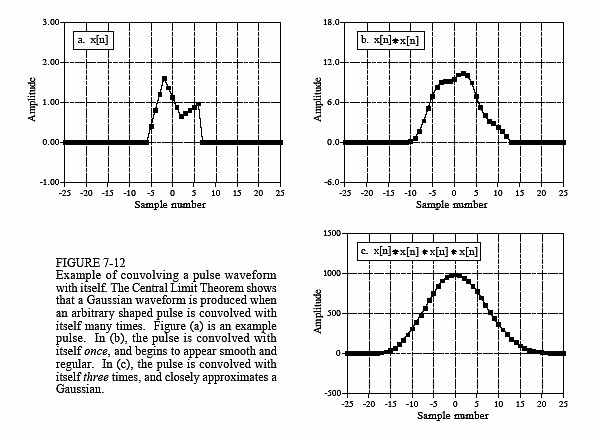
中心极限定理对于卷积有一个有趣的含义。如果脉冲状信号与其自身卷积多次,就会产生高斯信号。图 7-12 显示了一个示例。
- (a) 中的信号是不规则脉冲,故意选择与高斯脉冲非常不同的脉冲。
- 图 (b) 显示了该信号与其自身卷积一次的结果。
- 图 ( c ) (c) (c) 显示了该信号 与其自身卷积3次 的结果。即使只有三个卷积,波形看起来也非常像高斯分布。用数学术语来说,该过程很快就会收敛到高斯分布。所得高斯的宽度(即方程 2-7 或 2-8 中的 σ)等于原始脉冲的宽度(在方程 2-7 中表示为 σ)乘以卷积脉冲数的平方根。
11 相关性
相关性的概念最好用一个例子来说明。图 7-13 显示了雷达系统的关键元件。专门设计的天线在选定的方向上发射短脉冲无线电波能量。如果传播的波击中物体(例如图中的直升机),一小部分能量会反射回发射器附近的无线电接收器。发射的脉冲是我们选择的特定形状,例如本例中所示的三角形。
接收到的信号将由两部分组成:(1) 传输脉冲的移位和缩放版本,以及 (2) 由干扰无线电波、电子设备中的热噪声等产生的随机噪声。由于无线电信号以已知的速度传播,速率、光速、发射脉冲和接收脉冲之间的偏移是到被检测物体距离的直接测量。
这就是问题所在:给定某种已知形状的信号,确定该信号在另一个信号中的位置(或是否)出现的最佳方法是什么? 相关性就是答案。

相关性是一种与卷积非常相似的数学运算。正如卷积一样,相关使用两个信号来产生第三个信号。第三个信号称为两个输入信号的互相关。如果信号与其自身相关,则所得信号称为自相关。
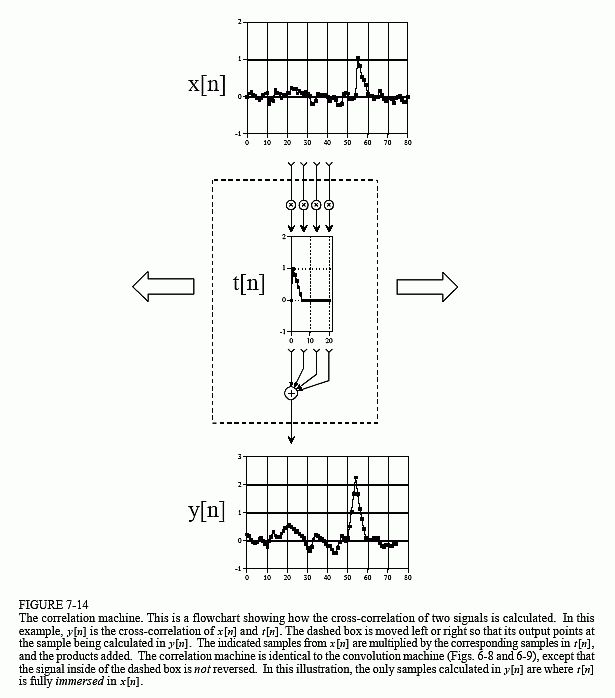
图7-14是类似的相关机的插图。接收到的信号 x[n] 和互相关信号 y[n] 固定在页面上。我们正在寻找的波形 t[n],通常称为目标信号,包含在相关机内。 y[n] 中的每个样本都是通过向左或向右移动相关机直到它指向正在处理的样本来计算的。接下来,来自接收信号的指示样本落入相关机,并与目标信号中的对应点相乘。然后,这些乘积的总和转移到互相关信号中的适当样本中。
互相关信号中每个样本的幅度是对在该位置处接收到的信号与目标信号的相似程度的度量。这意味着对于接收信号中存在的每个目标信号,互相关信号中将出现峰值。换句话说,当目标信号与接收信号中的相同特征对齐时,互相关值最大化。
如果目标信号包含负值样本怎么办? 没有什么变化。想象一下,相关机的位置使得目标信号与接收信号中的匹配波形完美对齐。当接收信号的样本落入相关机时,它们会与目标信号中的匹配样本相乘。忽略噪声,正样本将与其自身相乘,得到正数。同样,负样本将与其自身相乘,也会得到正数。即使目标信号完全为负,互相关的峰值仍将为正。
如果接收信号上存在噪声,则互相关信号上也会存在噪声。不可避免的事实是,随机噪声看起来在一定程度上类似于您可以选择的任何目标信号。互相关信号上的噪声只是测量这种相似性。除了该噪声之外,互相关信号中生成的峰值在其左右之间是对称的。即使目标信号不对称也是如此。此外,峰的宽度是目标信号宽度的两倍。请记住,互相关试图检测目标信号,而不是重新创建它。没有理由期望峰值看起来会像目标信号。
相关性是检测随机噪声中已知波形的最佳技术。也就是说,与任何其他线性系统相比,使用相关性产生的峰值高于噪声。 (为了完全正确,它仅适用于随机白噪声)。使用相关性来检测已知波形通常称为匹配滤波。
除了一点点差异之外,相关机和卷积机是相同的。卷积机内部的信号被左右翻转。这意味着采样数字:1、2、3…从右到左。在相关机中,不会发生这种翻转,并且样本沿正常方向运行。
由于信号反转是两个运算之间的唯一区别,因此可以使用与卷积相同的数学来表示相关性。这需要预翻转两个相关信号之一,从而取消卷积中固有的从左到右的翻转。例如,当 a[n] 和 b[n] 卷积生成 c[n] 时,方程为:a[n]✖️b[n] = c[n]。相比之下,a[n]和b[n]的互相关可以写成:a[n] * b[-n] = c[n]。也就是说,从左向右翻转 b[n] 是通过反转索引的符号(即 b[-n])来完成的。
不要让卷积和相关之间的数学相似性欺骗了你;它们代表非常不同的 DSP 程序。卷积是系统的输入信号、输出信号和脉冲响应之间的关系。相关性是在噪声背景中检测已知波形的一种方法。类似的数学只是一个方便的巧合。
这篇关于信号系统之卷积性质的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








