求解数独-舞蹈链求解

2024-02-17 06:50
文章标签 求解 数独 舞蹈

本文主要是介绍求解数独-舞蹈链求解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录
  • 前言
  • 我的代码
    • 代码讲解
    • 运行结果
  • 舞蹈链求解数独
  • 总结

前言

数独这个游戏很适合锻炼大脑思考，由于规则很简单，因此很适合我写代码拿来破解。所以就有了这篇随笔了。
首先我想通过自己的思考完成数独的求解，然后再到网上抄答案。提供一个【在线玩数独】的网站。

我的代码

代码讲解

    我想通过自己的思路来求解，虽然网上肯定有非常巧妙高效的解法。因此我安装了HoDoKu这个软件，这个软件会分析当前数独每个待填格子可能存在的值，目前我发现Naked Or Hiden Single这2中是最容易找出来的，找出来了该位置就必填那个数。下图是一个例子，表示裸露的单个数字，该位置只有一种可能值。经过仔细研究,我得出了2个原则：

  1. 当前位置只有一种可能值，则优先填入。
  2. 当前位置的可能值在当前行列宫格唯一，那么这个值是隐藏的单个，也是必填的。

    有了上述2个原则，那么我必须有一种算法计算每一个待填单元格可能填入的数据。其实很简单，只需要遍历这些代填的位置，然后遍历当前行列所在宫格，去掉已经确定的值，剩下的就是待填值。
    经过上面的计算也只能将待填位置确认值填好，但是剩下有可能存在多个值且无法确定。因此我首先想到的就是暴力破解法，假设代填位置为其中一个可能值，由此继续填数字，每次填入数字后再进行一次上面找已确定单个数，如果无法继续，或者得到某个位置没有可能填入数据则说明假设出错，恢复上一次保存的状态，继续假设下一个可能值。
    下面就贴上我的代码，其中保存状态用了栈结构，每次缓存则压栈，恢复则弹栈：

package mainimport ("container/list""flag""fmt""log""os""syscall""time"
)const Length = 9 /* 数独长宽都是9 *//*MySudokuData
* 下面这个结构有点复杂
* num:  当前位置数据,包括初始值,已经填写的值
* cnt:  标识该位置可能数的个数
* flag: 初始时和num相同,只是在结果打印时区别初始值和计算得到值颜色
* may:  该数组记录当前位置可能值,总是从数组头开始
**/
type MySudokuData struct {num, cnt, flag int         /* 点位具体值,可能值的个数,该位置需要填值 */may            [Length]int /* 记录点位可能的值 */
}/*MyMayPos
* 下面结构保存存在多个可能值的位置
* pos:  记录可能值的坐标(其中i表示多少行,j表示多少列)
* cnt:  记录这些坐标个数
**/
type MyMayPos struct {pos [Length * Length]struct {i, j int /* 缓存待定位置i,j值 */}cnt int /* 待定位置个数 */
}/*MyCacheData
* 总体的数据结构
* data:  记录9*9的81个点位数据
* pos:   表示可能值的数据
* dot:   在计算时表示当前假设到哪个可能点
* may:   在计算时表示dot的点找到哪个可能值
**/
type MyCacheData struct {data     [Length][Length]MySudokuData /* 缓存整个数独 */pos      MyMayPos                     /* 缓存当前可能位置 */dot, may int                          /* 缓存第几个可能点,和该点第几个可能值 */
}var SudokuData MyCacheData /* 得到数独数据,和每个空位可能值,用于计算 */func init() {fr := flag.String("f", "Sudoku.txt", "input data file!")flag.Parse()byt, err := os.ReadFile(*fr)if err != nil {log.Fatal(err.Error())}var i, j, cnt, tmp intfor _, v := range byt {if tmp = int(v - '0'); tmp >= 0 && tmp <= 9 { /* 只处理文件中数字0~9 */SudokuData.data[i][j].num = tmpSudokuData.data[i][j].flag = tmpif cnt++; j < 8 {j++} else {i++j = 0}}}if cnt != 81 { /* 无论如何必须要有81个输入 */log.Fatal("输入文件不正确!")}
}/**
* 主程序入口
* http://aperiodic.net/phil/scala/s-99/
**/
func main() {var (pos, may, x, y, cnt intCacheData           = list.New()  /* 缓存数据栈 */TmpElement          *list.Element /* 缓存链表元素 */tStart              = time.Now()  /* 开始时间 */)FlushMayNum()                 /* 初始刷新一下可能值 */for false == GameComplete() { /* 如果没有完成则一直继续计算 */for ; pos < SudokuData.pos.cnt; pos++ { /* 遍历可能点 */x, y = SudokuData.pos.pos[pos].i, SudokuData.pos.pos[pos].jfor ; may < SudokuData.data[x][y].cnt; may++ { /* 遍历可能点中可能填写的值 */SudokuData.dot, SudokuData.may = pos, mayCacheData.PushFront(SudokuData) /* 保存当前状态到栈中 */SudokuData.data[x][y].num = SudokuData.data[x][y].may[may] /* 数据中填写可能值 */cnt++if FlushMayNum() { /* 进行一次寻找,返回true表示还能继续找 */pos, may = 0, 0goto NextGameLoop /* 数据已经重排,所以要重新遍历 */} /* 下面是else部分 *//* 如果找到了一个没有可能值的位置,从栈顶取数据,从下一个值开始遍历 */if TmpElement = CacheData.Front(); TmpElement == nil { /* 取栈顶元素,计算下一个可能值 */return /* 栈中没有数据,无解 */}SudokuData = TmpElement.Value.(MyCacheData) /* 恢复上次状态 */CacheData.Remove(TmpElement)                /* 移除栈顶状态 */}}/* 下面表示通过上面的计算,把所有可能点的可能值遍历,还是无法得到结果 */if TmpElement = CacheData.Front(); TmpElement == nil { /* 取栈顶元素,计算下一个可能值 */return /* 栈中没有数据,无解 */}SudokuData = TmpElement.Value.(MyCacheData) /* 恢复上次状态 */CacheData.Remove(TmpElement)                /* 移除栈顶状态 */pos, may = SudokuData.dot, SudokuData.may+1 /* may从下一个开始 */NextGameLoop: /* 重排的数据继续计算 */}fmt.Println("计算耗时 :", time.Since(tStart))PrintSudoku()       /* 完成后打印数独 */_, _ = fmt.Scanln() /* 避免一闪而逝 */
}/*FlushMayNum
* x横坐标,向下递增
* y纵坐标,向右递增
* 如果运行过程中有空位只有唯一值,那么填好值,再刷新一次
* 该方法结束后,空位一定存在多个可能值
* 返回false表示有位置无解,返回true表示所有位置都有多个解
**/
func FlushMayNum() bool {var i, j, k, t, x, y, tmpMay, flagBreak, xS, xE, yS, yE intStartLoop: /* 如果结果中有唯一值的位置,则重新计算 */SudokuData.pos.cnt = 0 /* 待定位置从0计数 */for i = 0; i < Length; i++ {for j = 0; j < Length; j++ {if 0 == SudokuData.data[i][j].num { /* 空位才需要刷新可能值 */for k = 0; k < Length; k++ {SudokuData.data[i][j].may[k] = k + 1 /* 为可能值赋初值 */} /* 初始i,j位置默认可能存在的数值 */for k = 0; k < Length; k++ {if t = SudokuData.data[i][k].num; t > 0 { /* 遍历行 */SudokuData.data[i][j].may[t-1] = 0 /* 从可能中剔除该数字 */}if t = SudokuData.data[k][j].num; t > 0 { /* 遍历列 */SudokuData.data[i][j].may[t-1] = 0 /* 从可能中剔除该数字 */}} /* 上面循环剔除行列的值 */xS = i / 3 * 3 /* 所在宫格x起始 */xE = xS + 3    /* 所在宫格x结束 */yS = j / 3 * 3 /* 所在宫格y起始 */yE = yS + 3    /* 所在宫格y结束 */for ; xS < xE; xS++ {for k = yS; k < yE; k++ {if t = SudokuData.data[xS][k].num; t > 0 {SudokuData.data[i][j].may[t-1] = 0 /* 从可能中剔除该数字 */}}} /* 上面双层循环遍历所在宫格 *//* 下面将可用值左移,保证有效值从数组头开始 */for k, SudokuData.data[i][j].cnt = 0, 0; k < Length; k++ {if t = SudokuData.data[i][j].may[k]; t > 0 {SudokuData.data[i][j].may[SudokuData.data[i][j].cnt] = tSudokuData.data[i][j].cnt++ /* 将可能的值移动到前面 */}}if 0 == SudokuData.data[i][j].cnt {return false /* 该位置没有解 */}if 1 == SudokuData.data[i][j].cnt { /* 如果当前位置只有一种可能值 */SudokuData.data[i][j].num = SudokuData.data[i][j].may[0] /* 将该值填入数组中 */goto StartLoop                                           /* 重新刷新可能值数据 */}/* 下面用插入排序发将每个点可能的个数从小到大添加到MayPos中 */// for k = 0; k < SudokuData.pos.cnt; k++ {//	if SudokuData.data[i][j].cnt < SudokuData.data[SudokuData.pos.pos[k].i][SudokuData.pos.pos[k].j].cnt {//		break /* 找到位置,由小到达的排序,可以让循环次数减少 *///	}// }// for t = SudokuData.pos.cnt; t > k; t-- { /* 上面找到位置,该位置右边数据集体右移一位 *///	SudokuData.pos.pos[t].i, SudokuData.pos.pos[t].j = SudokuData.pos.pos[t-1].i, SudokuData.pos.pos[t-1].j// }// SudokuData.pos.pos[k].i, SudokuData.pos.pos[k].j = i, j// SudokuData.pos.cnt++ /* 可能点个数加1 */SudokuData.pos.pos[SudokuData.pos.cnt].i, SudokuData.pos.pos[SudokuData.pos.cnt].j = i, jSudokuData.pos.cnt++ /* 可能点个数加1 */} /* end if 0 == SudokuData[i][j].num { */} /* end j */} /* end i */flagBreak = 0/* 上面得到一个局面,及可能点一定有多个值,下面找隐藏的只有一个解的位置 */for i = 0; i < SudokuData.pos.cnt; i++ { /* 遍历每个可能点位置 */x, y = SudokuData.pos.pos[i].i, SudokuData.pos.pos[i].j /* 得到该点位置 */for j = 0; j < SudokuData.data[x][y].cnt; /* 不会执行到这里 j++ */ {tmpMay = SudokuData.data[x][y].may[j] /* 找这个可能值,看看是否为隐藏单个 */for k = 0; k < Length; k++ {if t = SudokuData.data[x][k].num; t == 0 { /* 遍历行中不确定格子 */for ; t < SudokuData.data[x][k].cnt; t++ {if tmpMay == SudokuData.data[x][k].may[t] {goto NextFlagX /* 这个可能值和在当前行不唯一 */}}}} /* 在行上找相同可能值 */SudokuData.data[x][y].num = tmpMay /* 这个值在行上可能值中是唯一,填值并重新填值 */flagBreak = 1breakNextFlagX:for k = 0; k < Length; k++ {if t = SudokuData.data[k][y].num; t == 0 { /* 遍历列中不确定格子 */for ; t < SudokuData.data[k][y].cnt; t++ {if tmpMay == SudokuData.data[k][y].may[t] {goto NextFlagY /* 这个可能值和在当前列不唯一 */}}}} /* 在列上找相同可能值 */SudokuData.data[x][y].num = tmpMay /* 这个值在行上可能值中是唯一,填值并重新填值 */flagBreak = 1breakNextFlagY:xS = x / 3 * 3 /* 所在宫格x起始 */xE = xS + 3    /* 所在宫格x结束 */yS = y / 3 * 3 /* 所在宫格y起始 */yE = yS + 3    /* 所在宫格y结束 */for ; xS < xE; xS++ {for k = yS; k < yE; k++ {if t = SudokuData.data[xS][k].num; t == 0 {for ; t < SudokuData.data[xS][k].cnt; t++ {if tmpMay == SudokuData.data[xS][k].may[t] {goto NextFlagZ /* 这个可能值和在当前列不唯一 */}}}}}SudokuData.data[x][y].num = tmpMay /* 这个值在行上可能值中是唯一,填值并重新填值 */flagBreak = 1breakNextFlagZ:}}if 1 == flagBreak {goto StartLoop}for i = 1; i < SudokuData.pos.cnt; i++ {x, y = SudokuData.pos.pos[i].i, SudokuData.pos.pos[i].jtmpMay = SudokuData.data[x][y].cntfor j = i - 1; j >= 0 && SudokuData.data[SudokuData.pos.pos[j].i][SudokuData.pos.pos[j].j].cnt > tmpMay; j-- {SudokuData.pos.pos[j+1].i = SudokuData.pos.pos[j].iSudokuData.pos.pos[j+1].j = SudokuData.pos.pos[j].j}SudokuData.pos.pos[j+1].i = xSudokuData.pos.pos[j+1].j = y}/* 下面打印可能点个数由少到多的排序 */// for i = 0; i < SudokuData.pos.cnt; i++ {//	fmt.Println(SudokuData.pos.pos[i], SudokuData.data[SudokuData.pos.pos[i].i][SudokuData.pos.pos[i].j])// }// fmt.Print("\n\n\n")// os.Exit(0)return true
}/*PrintSudoku
* 打印数独
* 这里需要win32api
* 将计算得到的数据上不同颜色
**/
func PrintSudoku() {var (i, j, tmp int)fmt.Println(" ---------+---------+---------")for i = 0; i < Length; i++ {fmt.Print("|")for j = 0; j < Length; j++ {if tmp = SudokuData.data[i][j].num; tmp > 0 {if 0 == SudokuData.data[i][j].flag { /* 该位置是计算得到的,标红色 */mSetConsoleTextAttribute(syscall.Stdout, 0x04|0x08)}fmt.Printf(" %d ", tmp) /* 下面把前景色重置为白色 */mSetConsoleTextAttribute(syscall.Stdout, 0x04|0x02|0x01)} else {fmt.Print(" . ")}if j == 2 || j == 5 {fmt.Print("|")}}switch i {case 2, 5:fmt.Print("|\n|---------+---------+---------|\n")case 0, 1, 3, 4, 6, 7:fmt.Println("|\n|         |         |         |")}}fmt.Println("|\n ---------+---------+---------")
}/*GameComplete
* 判断当前成功没
* 如果游戏完成则返回true
* 否则没有完成则返回false
**/
func GameComplete() bool {var i, j intfor i = 0; i < Length; i++ {for j = 0; j < Length; j++ {if 0 == SudokuData.data[i][j].num {return false /* 数独中存在没有完成的位置,则游戏还要继续 */}}}return true /* 所有位置都完成 */
}var setConsoleTextAttribute = syscall.NewLazyDLL("kernel32.dll").NewProc("SetConsoleTextAttribute")func mSetConsoleTextAttribute(hConsoleOutput syscall.Handle, wAttributes uint16) bool {ret, _, _ := syscall.SyscallN(setConsoleTextAttribute.Addr(),uintptr(hConsoleOutput),uintptr(wAttributes))return ret != 0
}/**
* http://cn.sudokupuzzle.org/
* https://www.newdoku.com/zh/sudoku.php
* 上面是2个在线数独网站
* 技巧：http://www.conceptispuzzles.com/zh/index.aspx?uri=puzzle/sudoku/techniques
* 规则：http://www.conceptispuzzles.com/zh/index.aspx?uri=puzzle/sudoku/rules
**/

运行结果

可通过执行Sudoku.exe -f Sudoku.txt来求解文件中的数独数据。下面就是一道数独题，复制后保存到Sudoku.txt中。

0,0,0,0,7,0,0,0,8
0,2,0,8,0,0,0,0,0
8,0,0,0,0,9,5,0,4
0,0,4,0,0,5,0,0,1
0,0,1,0,0,0,0,0,7
0,0,0,6,0,0,0,8,0
1,9,0,0,0,0,4,0,0
0,0,6,0,5,0,0,0,0
5,7,0,0,0,0,3,0,0

下面是结果，白色是题目数字，红色部分是答案：

数独结果

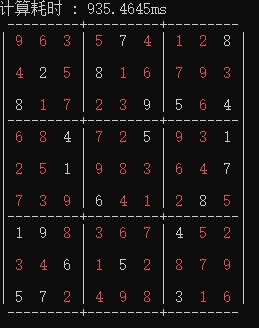
上面的方案效率在应对简单级别的也是很快的，基本毫秒级别。但是比较蛋疼的就是暴力求解存在把所有解遍历一遍的情况，那将遍历非常大，虽然我已经保证每次把确定的值填入，但仍然无可避免穷举的事实。测试过一个骨灰级的例子，用时44分钟。好了上面就把我自己的想法写成代码，并能正确得到结果，只是某些情况计算效率比较低，而且没有处理存在多个值的情况。

舞蹈链求解数独

求解数独最佳方案当然是舞蹈链了，优点就是不会占用多于空间，缓存和恢复状态非常快。跳跃的舞者，舞蹈链（Dancing Links）算法——求解精确覆盖问题 - 万仓一黍 - 博客园 讲解舞蹈链算法实践——舞蹈链（Dancing Links）算法求解数独 - 万仓一黍 - 博客园 讲解如何用舞蹈链解数独
代码灵感主要来源于上面的博客，并且舞蹈链求解比较快，因此我也做了多解数组至少算2种结果
    舞蹈链求解的具体流程就参照上面博客吧，下面把我的代码贴上：

package mainimport ("flag""fmt""log""os""syscall""time"
)const (LenGrid    = 9                 /* 数独都有9行9列格子 */Length     = LenGrid * LenGrid /* 数独有81个元素 */NineDance  = 9 * Length        /* 81*9 创建出9个舞蹈链,分别代表填入的数字 */FourDance  = 4 * Length        /* 81*4 约束条件 */MinInitial = 1000000000        /* 最小min的初值 */
)type Node struct {r, c  int /* 标识第r行,第c列 */up    *Nodedown  *Nodeleft  *Noderight *Node
}var (SudokuData [Length + 1]int                /* 保存数独数据 */Mem1       [Length + 1]int                /* 保存数独结果1 */Mem2       [Length + 1]int                /* 保存数独结果2 */Mem        = &Mem1                        /* 用mem操作2个结果内的值 */Cnt        [FourDance + 1]int             /* 0-324  用于记录0-324列,这一列有多少个结点 */SCnt       = 0                            /* 记录数独结果个数,本程序最多找到2个就退出 */Head       Node                           /* 头结点 */All        [NineDance*FourDance + 99]Node /* 0-236294  构建729*324+99列的舞蹈链 */AllCnt     int                            /* 舞蹈链的游标 */Row        [NineDance]Node                /* 0-728  构建729列的舞蹈链，用于1-9的填入，每个数字用81列来表示 */Col        [FourDance]Node                /* 0-323  构建324列的舞蹈链，用于满足4个约束条件 */
)func init() {fr := flag.String("f", "Sudoku.txt", "input data file!")flag.Parse()byt, err := os.ReadFile(*fr)if err != nil {log.Fatal(err.Error())}var cnt = 0for _, v := range byt {if v >= '0' && v <= '9' {if cnt < Length { /* 数独只有81个元素 */SudokuData[cnt] = int(v - '0')}cnt++}}if cnt != Length { /* 无论如何只有81个数字输入 */log.Fatal("输入文件只能有81个数字!")}SudokuData[cnt] = MinInitial /* 标识结束符 */AllCnt = 1                   /* 舞蹈链从位置1开始 */Head.left = &Head  /* 头结点的左边是头结点 */Head.right = &Head /* 头结点的右边是头结点 */Head.up = &Head    /* 头结点的上面是头结点 */Head.down = &Head  /* 头结点的下面是头结点 */Head.r = NineDance /* 行数等于729 */Head.c = FourDance /* 列数等于324 */for cnt = 0; cnt < FourDance; cnt++ {Col[cnt].c = cnt          /* 324列舞蹈链 用0-323赋值给c */Col[cnt].r = NineDance    /* 把 729 赋给 r */Col[cnt].up = &Col[cnt]   /* 它的上面等于自己 */Col[cnt].down = &Col[cnt] /* 它的下面等于自己 */Col[cnt].left = &Head           /* 它的左边等于头结点 */Col[cnt].right = Head.right     /* 它的右边等于头结点的右边 */Col[cnt].left.right = &Col[cnt] /* 它的左边的右边等于自己 */Col[cnt].right.left = &Col[cnt] /* 它的右边的左边等于自己 */}for cnt = 0; cnt < NineDance; cnt++ {Row[cnt].r = cnt       /* 729行舞蹈链，行数等于i */Row[cnt].c = FourDance /* 列数等于324 */Row[cnt].left = &Row[cnt]  /* 它的左边等于自己 */Row[cnt].right = &Row[cnt] /* 它的右边等于自己 *//* 头结点下边行的编号从上到下是728到0 */Row[cnt].up = &Head          /* 它的上边等于头结点 */Row[cnt].down = Head.down    /* 它的下边等于头结点的下边 */Row[cnt].up.down = &Row[cnt] /* 它的上边的下边等于自己 */Row[cnt].down.up = &Row[cnt] /* 它的下边的上边等于自己 */}/* 访问所有行,数独舞蹈链中的第i行 表示 数独中的第r行第c列中填入数字val */for cnt = 0; cnt < NineDance; cnt++ {var (r   = cnt / 9 / 9 % 9 /* 0-80  r为0   81-161 r为1 …… 648-728 r为8    表示数独中的行    映射：舞蹈链行->数独行 */c   = cnt / 9 % 9     /* 0-8  c为0   9-17 c为1   18-26  c为2   ……   72-80为8  循环直至720-728为8  81个为一个周期   表示数独中的列  映射：舞蹈链行->数独列 */val = cnt%9 + 1       /* 0为1  1为2  2为3  ……  8为9   9个为一个周期   表示数字1-9   映射：舞蹈链行->1-9数字 */)if SudokuData[r*9+c] == 0 || SudokuData[r*9+c] == val { /* r表示第r行,c表示第c列，如果数独的第r行第c列是0-9 *//* 如果数独的第r行第c列是0号则它的所有行都建立舞蹈链结点 *//* 如果数独的第r行第c列是数字则它的指定行都建立舞蹈链结点 */Link(cnt, r*9+val-1)        /* 处理约束条件1：每个格子只能填一个数字    0-80列 */Link(cnt, Length+c*9+val-1) /* 处理约束条件2：每行1-9这9个数字只能填一个   81-161列 */tr := r / 3tc := c / 3Link(cnt, Length*2+(tr*3+tc)*9+val-1) /* 处理约束条件3：每列1-9的这9个数字都得填一遍 */Link(cnt, Length*3+r*9+c)             /* 处理约束条件4：每宫1-9的这9个数字都得填一遍 */}}/* 把728个行结点全部删除 */for cnt = 0; cnt < NineDance; cnt++ {Row[cnt].left.right = Row[cnt].right /* 每一行左边的右边等于行数的右边 */Row[cnt].right.left = Row[cnt].left  /* 每一行右边的左边等于行数的左边 */}
}/**
* 主程序入口
* http://aperiodic.net/phil/scala/s-99/
* https://www.newdoku.com/zh/sudoku.php
* http://www.cnblogs.com/grenet/p/3145800.html 讲解舞蹈链
* http://www.cnblogs.com/grenet/p/3163550.html 讲解如何用舞蹈链解数独
**/
func main() {var tStart = time.Now() /* 开始时间 */Solve(1)var useTime = time.Since(tStart) /* 计算用时 *//* 下面打印数独,初始化数据和打印都不计入运算时间 */switch SCnt {case 2:PrintSudoku(1)PrintSudoku(2)fmt.Print("  2个或者多个解的数独")case 1:PrintSudoku(1)fmt.Print("  1个解的数独")default:fmt.Print("  此数独无解")}fmt.Println(",计算耗时:", useTime)_, _ = fmt.Scanln() /* 避免一闪而逝 */
}/*Link用链表解释就是一直插在第一个结点，以前的结点右推。第r行,第c列
*/
func Link(r, c int) {Cnt[c]++          /* 第c列的结点增加了一个 */t := &All[AllCnt] /* 将指针指向下一个，就像线性表添加元素一样 */AllCnt++t.r = r /* t的行数等于r */t.c = c /* t的列数等于c */t.left = &Row[r]       /* t的左边等于第r行结点 */t.right = Row[r].right /* t的右边等于第r行结点的右边 */t.left.right = t       /* t的左边的右边等于t */t.right.left = t       /* t的右边的左边等于t */t.up = &Col[c]       /* t的上边等于第c列结点 */t.down = Col[c].down /* t的下边等于第c列下边 */t.up.down = t        /* t的上边的下边等于t */t.down.up = t        /* t的下边的上边等于t */
}/*Remove
* 删除这列的结点和结点所在行的结点
**/
func Remove(c int) {var t, tt *Node/* 删除列结点 */Col[c].right.left = Col[c].left  /* 该列结点的右边的左边等于该列结点的左边 */Col[c].left.right = Col[c].right /* 该列结点的左边的右边等于该列结点的右边 */for t = Col[c].down; t != &Col[c]; t = t.down { /* 访问该列的所有结点 直到回到列结点 */for tt = t.right; tt != t; tt = tt.right { /* 访问该列所有结点所在的每一行 */Cnt[tt.c]-- /* 该列的结点减少一个 *//* 删除该结点所在行中的一个结点 */tt.up.down = tt.down /* 该结点的上边的下边等于该结点的下边 */tt.down.up = tt.up   /* 该结点的下边的上边等于该结点的上边 */}/* 删除该结点 */t.left.right = t.right /* t的左边的右边等于t的右边 */t.right.left = t.left  /* t的右边的左边等于t的左边 */}
}/*Resume
* 恢复一个节点
**/
func Resume(c int) {var t, tt *Node/* 遍历该列结点 */for t = Col[c].down; t != &Col[c]; t = t.down {t.right.left = t /* 恢复t结点 */t.left.right = t /* 恢复t结点 */for tt = t.left; tt != t; tt = tt.left { /* 一直访问左边，直到回到t */Cnt[tt.c]++tt.down.up = tttt.up.down = tt}}Col[c].left.right = &Col[c]Col[c].right.left = &Col[c]
}/*Solve
* 计算数独
**/
func Solve(k int) {var (t, tt *Nodemin   = MinInitialtc    int)if Head.right == &Head { /* 得到一个数独结果 */if SCnt == 0 { /* 首次得到结果 */for tc = 0; tc <= Length; tc++ {Mem2[tc] = Mem1[tc]}Mem = &Mem2 /* 将下一次计算的结果写到Mem2中 */}SCnt++ /* 这里第一种解决方案得到后，返回继续 选行 来看有没有第二种解决方案 */return}// fmt.Println(k) /* 打印每次查找的行 *//* 从头结点开始一直向右 直到回到头结点挑选结点数量最小的那一行，如果数量小于等于1直接用这行 */for t = Head.right; t != &Head; t = t.right {if Cnt[t.c] < min {min = Cnt[t.c]tc = t.cif min <= 1 {break}}}/* min==0的时候会把列删除然后再把列恢复然后返回，说明之前选错了行导致出现了结点为0的列，重新往下选择一行。 */Remove(tc) /* 移除这一列 *//* 扫描这一列 直到 回到列结点 */for t = Col[tc].down; t != &Col[tc]; t = t.down {Mem[k] = t.r /* mem[k]存储t的行数，最后可以通过行数来推断数独的几行几列填入了哪个数字 *//* 如果没有这一步的话，在下面for循环的过程中会陷入死循环 */t.left.right = t /* 经检查这两个指针所指向的地址不同 *//* 开始访问t的右边 直到回到t。但是由于t在remove(tc)的过程中左右被跳过，所以tt!=t可能会一直成立，所以需要上一步来保证能回到t */for tt = t.right; tt != t; tt = tt.right {Remove(tt.c) /* 移除该行中所有带结点的列 */}/* 等到该行的所有结点都删除以后，把t结点彻底地删除 */t.left.right = t.rightSolve(k + 1)   /* 给下一个找行 */if SCnt >= 2 { /* 这里找到2个解就退出 */return}/* 同上，避免死循环 */t.right.left = t/* 恢复所有被删除的列 */for tt = t.left; tt != t; tt = tt.left {Resume(tt.c)}t.right.left = t.left /* 恢复t结点 */}Resume(tc) /* 恢复tc列,一旦跑出来了说明之前选错了行，且如果一直回溯到一开始然后没有更多的行可以选择且sCnt为0就说明没有解决方案 */
}/*PrintSudoku
* 打印数独
* 这里需要win32api
* 将计算得到的数据上不同颜色
**/
func PrintSudoku(res int) {var (i, tmp intans    [Length]intmem    = &Mem1)if res == 2 { /* 确定打印那个结果 */mem = &Mem2}for i = 1; i <= Length; i++ {ans[mem[i]/9%Length] = mem[i]%9 + 1}fmt.Println(" ---------+---------+---------")for i = 1; i <= Length; i++ {if i%3 == 1 {fmt.Print("|")}if tmp = ans[i-1]; tmp > 0 {if SudokuData[i-1] == 0 { /* 该位置是计算得到的,标红色 */mSetConsoleTextAttribute(syscall.Stdout, 0x04|0x08)}fmt.Printf(" %d ", tmp) /* 下面把前景色重置为白色 */mSetConsoleTextAttribute(syscall.Stdout, 0x04|0x02|0x01)} else {fmt.Print(" . ")}if i < Length {if i%27 == 0 {fmt.Println("|\n|---------+---------+---------|")} else if i%9 == 0 {fmt.Println("|\n|         |         |         |")}}}fmt.Println("|\n ---------+---------+---------")
}var setConsoleTextAttribute = syscall.NewLazyDLL("kernel32.dll").NewProc("SetConsoleTextAttribute")func mSetConsoleTextAttribute(hConsoleOutput syscall.Handle, wAttributes uint16) bool {ret, _, _ := syscall.SyscallN(setConsoleTextAttribute.Addr(),uintptr(hConsoleOutput),uintptr(wAttributes))return ret != 0
}

用该方法求解【世界最难数独】,速度也是嗖嗖的：

并且使用舞蹈链解法是可以解多个答案的数独，不过有多解的数独严格来讲不能称之为数独。

递归求解

参考网上别人的方案，编写如下通过递归方式求解数独。

package mainimport ("errors""flag""fmt""os""syscall""time"
)func main() {input := flag.String("f", "input.txt", "")flag.Parse()s, err := NewSudoku(*input)if err != nil {panic(err)}tStart := time.Now()s.Solve()useTime := time.Since(tStart)s.Print()fmt.Printf("计算耗时: %s,尝试次数: %d\n", useTime, s.cnt)
}const SudokuLineLen = 9 /* 数独长宽都是9 */type sudoku struct {data, org [SudokuLineLen][SudokuLineLen]intcnt       intsetConsoleTextAttribute uintptr
}func NewSudoku(f string) (*sudoku, error) {data, err := os.ReadFile(f)if err != nil {return nil, err}var (s = &sudoku{setConsoleTextAttribute: syscall.NewLazyDLL("kernel32.dll").NewProc("SetConsoleTextAttribute").Addr(),}cnt, i, j int)const sudokuMaxNumber = SudokuLineLen * SudokuLineLenfor _, v := range data {if v >= '0' && v <= '9' {s.data[i][j] = int(v - '0')s.org[i][j] = s.data[i][j]if cnt++; cnt == sudokuMaxNumber {break}if j < 8 {j++} else {i++j = 0}}}if cnt < sudokuMaxNumber {return nil, errors.New("必须读入81个数字")}return s, nil
}func (s *sudoku) Solve() bool {for i := 0; i < SudokuLineLen; i++ {for j := 0; j < SudokuLineLen; j++ {if s.data[i][j] != 0 {continue // 跳过原始输入数字}for k := 1; k <= 9; k++ {// 尝试为这个位置放置1-9这些数字,放一次就判断一次是否合法if s.IsValidSudoku(i, j, k) {s.cnt++ // 尝试放置k的次数s.data[i][j] = k // i,j位置放k目前合法if s.Solve() {return true // 递归下一个可填写位置}s.data[i][j] = 0 // i,j位置放k不合法,回溯其他解}}// 9个数字都尝试还不行则无解,返回失败避免无限递归return false}}// 遍历完没有返回false,则说明找到合适位置的数值return true
}func (s *sudoku) IsValidSudoku(row, col, val int) bool {for i := 0; i < 9; i++ {if s.data[row][i] == val {return false // 同行有重复值}if s.data[i][col] == val {return false // 同列有重复值}}sr, sc := (row/3)*3, (col/3)*3for i := sr; i < sr+3; i++ {for j := sc; j < sc+3; j++ {if s.data[i][j] == val {return false // 同一个九宫格有重复值}}}return true
}func (s *sudoku) Print() {fmt.Println(" ---------+---------+---------")for i := 0; i < SudokuLineLen; i++ {for j := 0; j < SudokuLineLen; j++ {if j%3 == 0 {fmt.Print("|")}if tmp := s.data[i][j]; tmp > 0 {if s.org[i][j] == 0 {s.SetConsoleTextAttribute(0x04 | 0x08)fmt.Printf(" %d ", tmp)s.SetConsoleTextAttribute(0x04 | 0x02 | 0x01)} else {fmt.Printf(" %d ", tmp)}} else {fmt.Print(" . ")}}if i == SudokuLineLen-1 {fmt.Println("|\n ---------+---------+---------")} else if (i+1)%3 == 0 {fmt.Println("|\n|---------+---------+---------|")} else {fmt.Println("|\n|         |         |         |")}}
}func (s *sudoku) SetConsoleTextAttribute(wAttributes uint16) {_, _, _ = syscall.SyscallN(s.setConsoleTextAttribute,uintptr(syscall.Stdout), uintptr(wAttributes))
}/**
* http://cn.sudokupuzzle.org/
* https://www.newdoku.com/zh/sudoku.php
* 上面是2个在线数独网站
* 技巧：http://www.conceptispuzzles.com/zh/index.aspx?uri=puzzle/sudoku/techniques
* 规则：http://www.conceptispuzzles.com/zh/index.aspx?uri=puzzle/sudoku/rules
**/

总结

    算法真是奇妙的东西，出了可以解决生活和工作中的各种问题，提高效率，还能破解游戏。虽然玩数独很有趣，破解数独似乎对于我们这些程序员来说更刺激吧。

这篇关于求解数独-舞蹈链求解的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/716993。

相关文章

2024 年高教社杯全国大学生数学建模竞赛题目——2024 年高教社杯全国大学生数学建模竞赛题目的求解

2024 年高教社杯全国大学生数学建模竞赛题目——2024 年高教社杯全国大学生数学建模竞赛题目的求解

2024 年高教社杯全国大学生数学建模竞赛题目 （请先阅读“ 全国大学生数学建模竞赛论文格式规范 ”） 2024 年高教社杯全国大学生数学建模竞赛题目 随着城市化进程的加快、机动车的快速普及， 以及人们活动范围的不断扩大，城市道 路交通拥堵问题日渐严重，即使在一些非中心城市，道路交通拥堵问题也成为影响地方经 济发展和百姓幸福感的一个“痛点”，是相关部门的棘手难题之一。 考虑一个拥有知名景区
阅读更多...
基于SA模拟退火算法的多车辆TSP问题求解matlab仿真

基于SA模拟退火算法的多车辆TSP问题求解matlab仿真

目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.本算法原理 5.完整程序 1.程序功能描述        基于SA模拟退火算法的多车辆TSP问题求解matlab仿真，三个车辆分别搜索其对应的最短路径，仿真后得到路线规划图和SA收敛曲线。 2.测试软件版本以及运行结果展示 MATLAB2022A版本运行 （完整程序运行后无水印）
阅读更多...
OpenGL/GLUT实践：流体模拟——数值解法求解Navier-Stokes方程模拟二维流体（电子科技大学信软图形与动画Ⅱ实验）

OpenGL/GLUT实践：流体模拟——数值解法求解Navier-Stokes方程模拟二维流体（电子科技大学信软图形与动画Ⅱ实验）

源码见GitHub：A-UESTCer-s-Code 文章目录 1 实现效果2 实现过程2.1 流体模拟实现2.1.1 网格结构2.1.2 数据结构2.1.3 程序结构1) 更新速度场2) 更新密度值 2.1.4 实现效果 2.2 颜色设置2.2.1 颜色绘制2.2.2 颜色交互2.2.3 实现效果 2.3 障碍设置2.3.1 障碍定义2.3.2 障碍边界条件判定2.3.3 障碍实现2.3.
阅读更多...
JD 1147：Jugs（一种用最少步骤求解的方法）

JD 1147：Jugs（一种用最少步骤求解的方法）

OJ题目：click here~~ 题目分析：九度上这道没有要求最少步数，只要得到最后结果即可AC ， bfs ， dfs都行。最少步骤的方法肯定也能AC啦，分析如下。 输入的三个数：a,b,n;> 由题不定方程ax+by=n必定有解> 如果b=n，则fill B即可，否则用试探法求出这样的两组解（a1，b1）及（a2，b2），其中a1 >0，b1<0；a1是满足方程的最小正整数；a2
阅读更多...
【2024全国大学生数学建模竞赛】B题 模型建立与求解（含代码与论文）

【2024全国大学生数学建模竞赛】B题 模型建立与求解（含代码与论文）

目录 1问题重述1.1问题背景1.2研究意义1.3具体问题 2总体分析3模型假设4符号说明（等四问全部更新完再写）5模型的建立与求解5.1问题一模型的建立与求解5.1.1问题的具体分析5.1.2模型的准备 目前B题第一问的详细求解过程以及对应论文部分已经完成！ - 晚上7-8点之前第二问完成 - 明天中文之前全部写完 按照提交论文的格式进行撰写！完整版请看文章最后！
阅读更多...
Java 快速求解x的x次幂结果为10

Java 快速求解x的x次幂结果为10

1.问题描述 如果x的x次幂结果为10（如图所示），你能计算出x的近似值吗？ 显然，这个值是介于2和3之间的一个数字。 可以使用牛顿迭代公式进行求解，因为是逼近算法可以大大减少运算次数 public static void main(String[] args) {int i = 0;double x1 = 2.5;while (true) {i++;//x^x - 10 = 0//这一步
阅读更多...
最值求解 | 管理类联考数学专项

最值求解 | 管理类联考数学专项

日期内容2024.9.5新建2024.9.6曦曦求最值完结 实数求最值至少至多抽屉原理工程问题线性规划一次性绝对值求最值 参考： b站跟着曦曦老师玩转【最值】
阅读更多...
2024数学建模国赛A题详细思路：基于空间几何运动学和优化模型matlab求解

2024数学建模国赛A题详细思路：基于空间几何运动学和优化模型matlab求解

2024数学建模国赛A题“板凳龙”闹元宵 2024高教社杯数学建模竞赛A题B题C题D题E题完整成品文章和全部问题的解题代码完整版本更新如下：https://www.yuque.com/u42168770/qv6z0d/rytbc1nelty1mu4o % 定义常量L_head = 3.41; % 龙头长度（米）L_body = 2.20; % 龙身长度（米）spiral_pitch =
阅读更多...
清华MEM作业-利用管理运筹学的分析工具slover求解最优解的实现 及 通过使用文件或者套节字来识别进程的fuser命令

清华MEM作业-利用管理运筹学的分析工具slover求解最优解的实现 及 通过使用文件或者套节字来识别进程的fuser命令

一、清华MEM作业-利用管理运筹学的分析工具slover求解最优解的实现         最近又接触了一些线性求解的问题，以前主要都是在高中数学里接触到，都是使用笔算，最后通过一些函数式得出最小或者最大值，最近的研究生学业上接触到了一个Excel solver分析工具，对这种线性求最优解的问题感觉使用起来真是得心应手。在使用这个工具前，EXCEL里需要先装上solver工具，装起来很也简单，网上
阅读更多...
【教学类-52-08】20240905动物数独（6宫格）一页2张任务卡，一页一个动物贴图卡，有答案

【教学类-52-08】20240905动物数独（6宫格）一页2张任务卡，一页一个动物贴图卡，有答案

背景需求： 前文提到6宫格数独的图片6*6=36图，如果将6张任务卡放在一个A4上，看上去6种动物很小，所以我换了一个word模板，变成了2张任务卡放在一个A4上。 【教学类-52-07】20240903动物数独（6宫格）一页2张任务卡，无答案-CSDN博客文章浏览阅读846次，点赞25次，收藏6次。【教学类-52-07】20240903动物数独（6宫格）一页2张任务卡，无答案https:
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2