AI - 碰撞避免算法分析(ORCA)

本文主要是介绍AI - 碰撞避免算法分析(ORCA)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

对比VO/RVO

ORCA算法检测碰撞的原理和VO/RVO基本一样的，只是碰撞区域的计算去掉了一定时间以外才可能发生的碰撞，因此碰撞区域的扇形去掉了前面的部分，由圆锥头变成了个圆

另一个最主要的区别是，求新的速度，是根据相对多个不同物体生成的半平面计算获得。
半平面：

上图里，u即之前VO和RVO求出的相对速度避免碰撞需要偏移的最短速度向量VO/RVO分析。VO/RVO里由于只考虑避障双方的两个物体，所以期望速度Vaopt加上了u之后，便获得了结果。在ORCA里，会考虑多个碰撞物体，因此会过Vaopt加上u/2之后的点，做u向量的垂直线，而获得一条直线。这条直线一侧所有的点(即ORCA半平面)表示的速度，都会让a不与b相撞。
对于多个碰撞物体，可以求出多个半平面，通过这些半平面的交集，来确定物体的新速度

论文理论的分析

具体的分析网上有挺多的，理论本身还是比较好理解的，这里直接转载别人的了ORCA(RVO2)算法优化整理版

源码分析

ORCA源码地址

RVOSimulator

RVOSimulator相当于整个碰撞避免逻辑的管理模拟器。
一些参数
timeStep_：管理器每次模拟的时间间隔，传入的基本就是游戏运行的每帧时间
kdTree_：一个数组结构的KD树，用来管理每个机器人的相邻目标
agents_：管理器控制的机器人
obstacles_：管理器控制的静态障碍物
主要函数：
addAgent：向管理器添加需要进行碰撞避免处理的机器人
doStep：模拟一次所有机器人碰撞避免处理：先构建kd树，计算每个机器人的相邻目标，在计算新的速度，然后更新位置

void RVOSimulator::doStep() {kdTree_->buildAgentTree();
#ifdef _OPENMP
#pragma omp parallel for
#endif /* _OPENMP */for (int i = 0; i < static_cast<int>(agents_.size()); ++i) {agents_[i]->computeNeighbors(kdTree_);agents_[i]->computeNewVelocity(timeStep_);}#ifdef _OPENMP
#pragma omp parallel for
#endif /* _OPENMP */for (int i = 0; i < static_cast<int>(agents_.size()); ++i) {agents_[i]->update(timeStep_);}globalTime_ += timeStep_;
}

KdTree

kd树的原理之前文章有分析过，这里先跳过了
KDTree

Agent

实际碰撞物的代理目标，可以每帧中把游戏实际物体的参数传入，通过RVOSimulator计算后，再取出对应代理目标的位置信息更新游戏实际物体
类似这样：

m_sim->setTimeStep(dt);
for(auto aiNode: _aiNodes) {int idx = aiNode->getId();Vec2 velocity = aiNode->getVelocity();m_sim->setAgentMaxSpeed(idx, 1/dt);m_sim->setAgentPrefVelocity(idx, Vector2(velocity.x * 1 / dt, velocity.y * 1 / dt));
}
m_sim->doStep();
for (auto aiNode : _aiNodes) {int idx = aiNode->getId();Vector2 velocity = m_sim->getAgentVelocity(idx);Vector2 v = m_sim->getAgentPosition(idx);aiNode->setVelocity(Vec2(velocity.x() * dt, velocity.y() * dt));aiNode->setPosition(Vec2(v.x(), v.y()));
}

Agent参数

agentNeighbors_：相邻的动态目标
obstacleNeighbors_：相邻的静态障碍物
orcaLines_：储存的半平面信息
newVelocity_：新的避障速度
*position_*位置
prefVelocity_：最佳目标速度
velocity_：当前速度
id_：唯一id
maxNeighbors_：最大避障邻居数(太遥远的过多邻居没有避障意义)
maxSpeed_：最大速度
neighborDist_：查找避障领据的判定位置(太遥远的目标没有避障意义)
radius_：物体半径
timeHorizon_：提前避障的时间，即只判定在一定时间范围内可能的碰撞
timeHorizonObst_：静态物体提前避障的时间

避障核心代码入口

void Agent::computeNewVelocity()

创建静态障碍物的ORCA半平面

其中障碍物的类：当前point_和下一个障碍物nextObstacle_的point_会构成一条直线，unitDir_是当前point_指向下一个point_的单位方向向量，isConvex_表示是否凹角

bool isConvex_;
Obstacle *nextObstacle_;
Vector2 point_;
Obstacle *prevObstacle_;
Vector2 unitDir_;

判断当前静态障碍直线在已处理半平面的右侧，且两个端点到半平面的距离大于物体的半径。因为新速度只能取半平面左侧，即下图中的情况，则新速度永远不会与当前处理的静态障碍直线相交。可以直接忽略

const Vector2 relativePosition1 = obstacle1->point_ - position_;
const Vector2 relativePosition2 = obstacle2->point_ - position_;
bool alreadyCovered = false;for (size_t j = 0; j < orcaLines_.size(); ++j) {if (det(invTimeHorizonObst * relativePosition1 - orcaLines_[j].point, orcaLines_[j].direction) - invTimeHorizonObst * radius_ >= -RVO_EPSILON && det(invTimeHorizonObst * relativePosition2 - orcaLines_[j].point, orcaLines_[j].direction) - invTimeHorizonObst * radius_ >=  -RVO_EPSILON) {alreadyCovered = true;break;}}

半平面的坐标计算都是以自身位置为坐标系计算。因此障碍物直线的坐标也要转换一下。即relativePosition1
代码里invTimeHorizonObst根据不同的判定时间，向量长度会有不同的缩放，但相对比例是不变的，分析的时候可以都当成1来处理，来忽略掉。
det(invTimeHorizonObst * relativePosition1 - orcaLines_[j].point, orcaLines_[j].direction)
这行代码是半平面的点到障碍物直线一个端点的向量，与半平面单位方向向量取叉积，因为叉积的模等于两矢量各自的模的积再乘以两矢量夹角的正弦，其中一个向量为单位矢量，则结果就是另一个向量到单位向量直线上的垂直距离。
>= -RVO_EPSILON 叉积大于0表示在向量逆时针方向,即新的障碍物直线端点在已处理的半平面右边

判定物体的坐标相对于障碍物直线在哪个方向

描述起来比较拗口，可以看上图，结合代码

const Vector2 obstacleVector = obstacle2->point_ - obstacle1->point_;
const float s = (-relativePosition1 * obstacleVector) / absSq(obstacleVector);
const float distSqLine = absSq(-relativePosition1 - s * obstacleVector);

(-relativePosition1 * obstacleVector) 求点积，两矢量模相乘，再乘夹角的余弦。
即 s = |-relativePosition1|*|obstacleVector| * cosθ / |obstacleVector|
s为物体坐标在障碍物直线上的投影点到障碍物直线起始点的长度，即上图中红色线段长度。s的大小可以表示此时物体在障碍物直线的左边，右边，还是两个端点之间
distSqLine 为物体坐标到障碍物直线的垂直记录，即上图中灰色线段长度

已经碰撞，对于物体相对于障碍物直线的不同碰撞点，做不同处理

if (s < 0.0f && distSq1 <= radiusSq) {

物体与障碍物直线起始点1，即左端点相撞，如果起始点1对应的是凸角的话，就将当前线放入要处理的半平面。至于凹角为什么不处理，我的理解是，如果是凹角的话，物体对于凹角的另一条线的s一定是在0-1之间，即在障碍物直线两个端点之一，处理的权重更大。

line.point = Vector2(0.0f, 0.0f);
line.direction = normalize(Vector2(-relativePosition1.y(), relativePosition1.x()));

因为静态障碍物是不会动的，因此半平面直接以物体自身为目标点，方向以垂直偏离碰撞点为目的，即上图中白色箭头。

if (s > 1.0f && distSq2 <= radiusSq)

物体与障碍物直线起始点2，即右端点相撞。和左端点类似，只是加了一个判断，就是下图中，obstacle2-unitDir在红线右侧的方向的话，就忽略这条障碍线的碰撞处理，以相邻边的障碍线处理为准

if (obstacle2->isConvex_ && det(relativePosition2, obstacle2->unitDir_) >= 0.0f)

if (s >= 0.0f && s < 1.0f && distSqLine <= radiusSq)

物体在障碍物两个端点间碰撞，比较简单，直接远离就行，下图红色区域即为新速度可选择区域

未碰撞，同样根据物体相对障碍物直线的不同位置，做不同处理

if (s < 0.0f && distSqLine <= radiusSq)

物体在障碍物左端点左边，如下图，并且不能是凹角，因为distSqLine <= radiusSq在这个情况下，如果是凹角的话，前一条障碍物直线一定会和物体已经碰撞，则先处理逃离碰撞直线的情况

接下来这段代码很关键，直接看很难理解，因为代码是直接写了拆解了多个步骤之后的数学公式

const float leg1 = std::sqrt(distSq1 - radiusSq);
leftLegDirection = Vector2(relativePosition1.x() * leg1 - relativePosition1.y() * radius_, relativePosition1.x() * radius_ + relativePosition1.y() * leg1) / distSq1;
rightLegDirection = Vector2(relativePosition1.x() * leg1 + relativePosition1.y() * radius_, -relativePosition1.x() * radius_ + relativePosition1.y() * leg1) / distSq1;

先说结论，leftLegDirection和rightLegDirection就是上图中绿色箭头所指的方向，两根线都是障碍物直线端点到圆的切线。


上图中红色箭头为向量，即障碍物直线左端点指向物体中心的
（-relativePosition1.x,-relativePosition1.y）
将该向量，逆时针旋转θ


将cosθ和sinθ代入，提取出分母 1/distSq1
最后将向量取反，解出来的结果就是
Vector2(relativePosition1.x() * leg1 - relativePosition1.y() * radius_, relativePosition1.x() * radius_ + relativePosition1.y() * leg1) / distSq1
获得了leftLegDirection，即上图中绿色箭头。
leftLegDirection同理，只不过是顺时针旋转

if (s > 1.0f && distSqLine <= radiusSq)

物体在障碍物右端点右边，与左边同理，略过
物体在障碍物直线之间
如果端点的角是凸角的情况下，就是leftLegDirection，rightLegDirection如下图所示

如果端点是凹角，则直接取平行于障碍物直线的方向

分析两根leg线是否会和障碍物直线的相邻边碰撞

if (obstacle1->isConvex_ && det(leftLegDirection, -leftNeighbor->unitDir_) >= 0.0f)

这行判断为true的情况是左端点相邻边的反方向在左leg的左边，如下图所示

因此速度域的边界不能以左leg为准，否则会和相邻边产生碰撞。直接更新左leg的方向为相邻边的反向。
右边同理

根据当前速度在速度障碍域的不同位置做不同处理

const float t = (obstacle1 == obstacle2 ? 0.5f : ((velocity_ - leftCutoff) * cutoffVec) / absSq(cutoffVec));
const float tLeft = ((velocity_ - leftCutoff) * leftLegDirection);
const float tRight = ((velocity_ - rightCutoff) * rightLegDirection);

上述t的含义表示了当前速度更靠近左右两边哪个端点。0-0.5更靠近左，0.5-1更靠近右，0.5正好居中。
tleft和tright就是判断当前速度投影到leg直线上，依次判断在leg射线上的哪个部分。小于0，则在leg射线的外部
判断物体是否以远离速度障碍域两个端点为目标

if ((t < 0.0f && tLeft < 0.0f) || (obstacle1 == obstacle2 && tLeft < 0.0f && tRight < 0.0f))
if (t > 1.0f && tRight < 0.0f)

如上图，速度点velocity_在rightCutoff-leftCutoff的投影不在向量内部，在leftLegDirection方向的投影也不在leftLegDirection内部(上图浅灰色直线)，则条件判断为true。
因此以远离端点为目标。
即灰色箭头为leftCutoff指向velocity_，长度为物体半径radius_，方向顺时针旋转90度即为红色箭头方向，由此够成的绿色区域为速度半平面

const float distSqCutoff = ((t < 0.0f || t > 1.0f || obstacle1 == obstacle2) ? std::numeric_limits<float>::infinity() : absSq(velocity_ - (leftCutoff + t * cutoffVec)));
const float distSqLeft = ((tLeft < 0.0f) ? std::numeric_limits<float>::infinity() : absSq(velocity_ - (leftCutoff + tLeft * leftLegDirection)));
const float distSqRight = ((tRight < 0.0f) ? std::numeric_limits<float>::infinity() : absSq(velocity_ - (rightCutoff + tRight * rightLegDirection)));

这三个变量是分别获取物体速度velocity_到两个leg以及障碍物直线的垂直距离，如果投影不在向量内部，则视作无穷大
判断物体是以远离速度障碍域哪个向量为目标即velocity_离cutoffVec和leftLegDirection和rightLegDirection哪个向量方向的直线最近，则远离哪个
根据*velocity_*的位置分别是下图三种情况

创建动态物体间的ORCA半平面

首先定义了几个相对参数
relativePosition：相对位置
relativeVelocity：相对速度
combinedRadius：自身半径视作0后，对方的相对半径

处理双方未碰撞的情况
即distSq > combinedRadiusSq
判断是否往小圆上计算u

if (dotProduct < 0.0F && dotProduct * dotProduct > combinedRadiusSq * wLengthSq)

先看下面这张图

图中红色箭头为代码里的向量w，绿线为combineRadiu，黄色线为relaticePosition
dotProduct = w * relativePosition求点积，如果小于0，说明w于relativePosition反向，可能需要往cutoff-circle处调整相对速度。
接下来只要确定证明红色箭头在绿线和黄色线之间,
即 ∠a < ∠b
==>> cosa > cosb
(cosa = dotProduct / |w| / |relativePosition|)
(cosb = combineRadius / |relativePosition|)
==>> dotProduct / |w| / |relativePosition| > combineRadius / |relativePosition|
==>> dotProduct > combineRadius * |w|
两边各平方
==>> dotProduct * dotProduct > combinedRadiusSq * wLengthSq

line.direction = Vector2(unitW.y(), -unitW.x());
u = (combinedRadius * invTimeHorizon - wLength) * unitW;

这段求得向量u的大小为下图中紫色线段长度，方向与w同向，半平面的方向为w顺时针旋转90°

判断往哪个leg方向计算u

if (det(relativePosition, w) > 0.0F)

求向量w和relativePosition的叉积，可以判断出w在relativePosition的左边还是右边，以此确定离哪个leg更近
求解半平面的方向，原理和前面静态障碍物求leftLegDirection、rightLegDirection方向是一样的，最终推导的公式也是类似的，这里不再重复了，根据不同leg求得的不同方向都在下图黑色箭头中标出来了

u = (relativeVelocity * line.direction) * line.direction - relativeVelocity;

求u的代码含义也在上图中标出来了

处理双方已碰撞的情况
本质也是往在圆的里面远离圆心，和未碰撞往小圆上计算u的原理一样

计算半平面的位置

line.point = velocity_ + 0.5F * u;

u计算出来后半平面的位置也就确定了

半平面交集求解

std::size_t linearProgram2(const std::vector<Line> &lines, float radius, const Vector2 &optVelocity, bool directionOpt, Vector2 &result) 

lines：所有半平面
radius：求解时的限定圆形半径(即物体最大速度)
optVelocity：当前物体的期望速度
directionOpt：默认false，执行linearProgram3(交集没有可行解)为true
result：当前步骤求出的最新速度

初始一下默认优化速度

if (directionOpt) {result = optVelocity * radius;
} else if (absSq(optVelocity) > radius * radius) {result = normalize(optVelocity) * radius;
} else {result = optVelocity;
}

遍历所有半平面，对每个半平面进行线性处理

if (det(lines[i].direction, lines[i].point - result) > 0.0F) 

只处理在当前半平面右侧的速度，左侧的速度本身就属于当前半平面的可行解。(注意叉积大于0虽然是逆时针方向。但是这里的是result指向lines[i].point，不是lines[i].point指向result)

线性规划求解

计算当前半平面的可行解，返回有无可行解

bool linearProgram1(const std::vector<Line> &lines, std::size_t lineNo,float radius, const Vector2 &optVelocity, bool directionOpt, Vector2 &result)

与linearProgram2参数一样，多了个 lineNo：当前处理的半平面索引id
这个行数是求可行解的核心代码，也是线性规划的过程

const float dotProduct = lines[lineNo].point * lines[lineNo].direction;

dotProduct就是向量lines[lineNo].point在lines[lineNo].direction上的投影长度。即上图中两个黑色线段的长度
圆的半径，即物体最大速度，必须在半平面的左边才能有解。即上图中粉色线必须大于紫色线。
紫色线标为len，即物体原点到半平面的垂直距离。
需要 radius > len
==>>radius * radius > len * len
(灰线长度为 |lines[lineNo].point|，根据勾股定理)
==>> sqr(radius) > absSq(lines[lineNo].point - sqr(dotProduct)
==>> sqr(radius) + sqr(dotProduct) - absSq(lines[lineNo].point > 0
==>> discriminant > 0
因此，下面代码表示无解退出

if (discriminant < 0.0f) {return false;
}

同时sqrtDiscriminant还表示上图黄色线段的长度
根据勾股定理
discriminant = sqr(radius) - sqr(len)
(sqr(len) = absSq(lines[lineNo].point - sqr(dotProduct))
==>> discriminant = sqr(radius) - absSq(lines[lineNo].point + sqr(dotProduct)

const float sqrtDiscriminant = std::sqrt(discriminant);
float tLeft = -dotProduct - sqrtDiscriminant;
float tRight = -dotProduct + sqrtDiscriminant;

tLeft和tRight即为上图中橙色和蓝色线段的长度。分别表示圆的两个交点到lines[lineNo].point的距离

比较已处理过的半平面

for (size_t i = 0; i < lineNo; ++i)

在当前 lineNo 半平面线性规划求解时，需要和之前处理过的半平面对比来缩小解的范围。最初的解范围是速度圆和半平面直线的两个交点范围。

if (std::fabs(denominator) <= RVO_EPSILON) {if (numerator < 0.0f) {return false;}else {continue;}
}

如果 lineNo 半平面 和 i 半平面平行即*det(lines[lineNo].direction, lines[i].direction)*约等于0，没有交点与当前范围对比，所以进行特殊处理
优因为当前 result 是在 lineNo 半平面右边， 所以如果 i 半平面在 lineNo 半平面左边
(det(lines[i].direction, lines[lineNo].point - lines[i].point) > 0)
一定是和 lineNo 反向，不会对当前求解范围有影响，因此 continue
但是 i 在 lineNo 右边的话这里的处理我有些没看懂， 如果 i 和 lineNo 反向的话，就没有可行解 return false 。但是 i 和 lineNo 如果同向的话，应该也是 continue。有大佬看懂的话方便留个评论解释一下吗。

const float t = numerator / denominator;

t 的含义是上图中两个半平面交点 o 到 当前半平面 lines[lineNo].point 的距离
因为
图中红色箭头为向量 lines[lineNo].point - lines[i].point
半平面的方向向量，长度都为1， 即 |lines[i].direction| = 1
叉积为两向量模乘正弦，因此 numerator 为上图中紫色线段长度，即 lines[lineNo].point 到 i 半平面的垂直距离
此时以两个半平面交点 o 为起点，画一个向量 lines[lineNo].direction ，可以得出 denominator 为上图中棕色线段的长度
又因为 |lines[lineNo].direction| = 1
并且 t / |lines[lineNo].direction| = numerator / denominator
即上图黄色线段

if (denominator >= 0.0F) {tRight = std::min(tRight, t);
} else {tLeft = std::max(tLeft, t);
}if (tLeft > tRight) {return false;
}

可行解最初的范围是大于 tLeft 小于 tRight
上图中，当 i 半平面的方向在 lineNo 半平面的右边。此时的可行解一定是大于交点 o 的区域
因此 denominator < 0 时， 需要 t 和 tLeft 对比谁更大。反之同理

const float t = lines[lineNo].direction * (optVelocity - lines[lineNo].point);
if (t < tLeft) {result = lines[lineNo].point + tLeft * lines[lineNo].direction;
} else if (t > tRight) {result = lines[lineNo].point + tRight * lines[lineNo].direction;
} else {result = lines[lineNo].point + t * lines[lineNo].direction;
}

如上图所示 t 代表了期望速度投射到半平面的阴影长度。根据 t 的不同位置求的不得解

if (directionOpt)

directionOpt 为 true 时，不会有可行解，直接根据期望速度与半平面方向是否同向来取交点

无可行解

void linearProgram3(const std::vector<Line> &lines, std::size_t numObstLines,std::size_t beginLine, float radius,Vector2 &result)

numObstLines：静态障碍物半平面的数量
beginLine：索引id，表示从哪条半平面开始无法求出可行解
另外三个参数和之前一样

if (det(lines[i].direction, lines[i].point - result) > distance) 

这行代码是求当前解到之后的每条无解半平面的垂直距离，以处理距离最远的半平面为准。我的理解是，离的最远的半平面，是碰撞机率最大的，因为他需要最大的调整速度，才能够调整回不碰撞的速度可行域

这个函数里的遍历都是去掉了静态障碍物的半平面的，因为静态障碍物自身是无法进行碰撞避免处理的

float determinant = det(lines[i].direction, lines[j].direction);
if (std::fabs(determinant) <= RVO_EPSILON) {if (lines[i].direction * lines[j].direction > 0.0f) {continue;}else {line.point = 0.5f * (lines[i].point + lines[j].point);}
}
else {line.point = lines[i].point + (det(lines[j].direction, lines[i].point - lines[j].point) / determinant) * lines[i].direction;
}

这段代码是，将当前处理的 j 半平面与已处理过的 i 半平面做对比。
如果两者平行并同向即重合了，则略过
如果平行但反向，获取两个半平面起始点的连线中点坐标
如果不平行，则获取两个半平面交点的坐标(推导原理和前面一样)

line.direction = normalize(lines[j].direction - lines[i].direction);

这行代码，是让已处理的半平面往 此当前处理的半平面，旋转一半的角度再取反
形成新的半平面交集，再进行求解

如上图，最初的三个半平面可行域是绿色阴影部分，没有公共交集。
i 半平面和 i+1 半平面都往 j 半平面方向旋转了一半夹角的长度，再取反，形成新的蓝色阴影区域，有公共交集。再进行线性规划求解

旋转的角度是根据 normalize(lines[j].direction - lines[i].direction) 设置的
我试着改变了 lines[i].direction 的长度，使旋转的角度不同

float len = 1;
line.direction = normalize(lines[j].direction - lines[i].direction * len);

len为1是旋转1/2的夹角，len越解决0，旋转后的半平面越接近 j 半平面，len越大，旋转后的半平面越近 i 半平面的反向。

演示效果

静态图

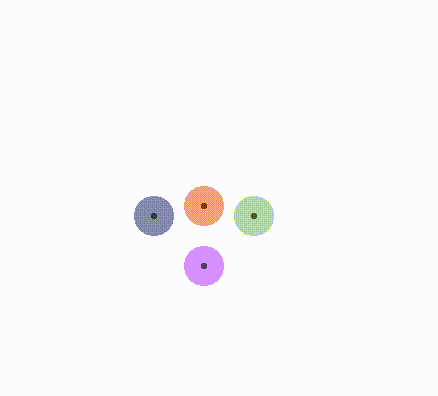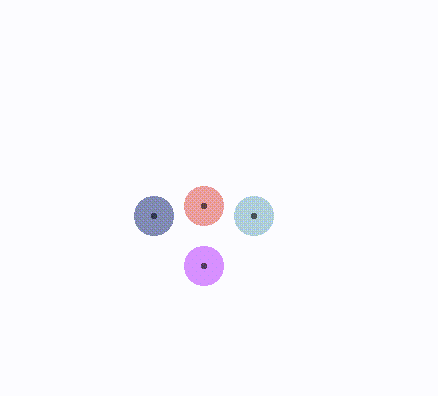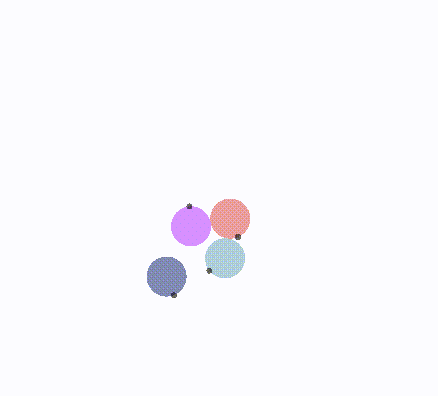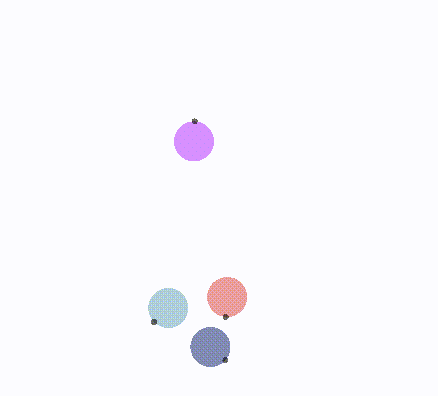
以下是几种设置不同旋转角度后，求得的速度，以四个球最下方的那个球为分析目标，
三根不同的射线就是三条半平面，此时的三个半平面是没有可行解的。球的黑点位置就是新的速度朝向。

设置不同len时的，物体的新速度朝向：
len = 1，旋转1/2角度

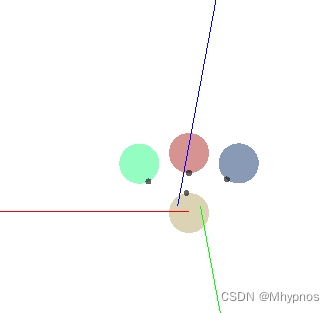
len = 0.5

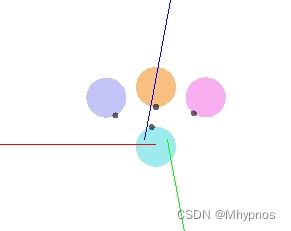
len = 0.1

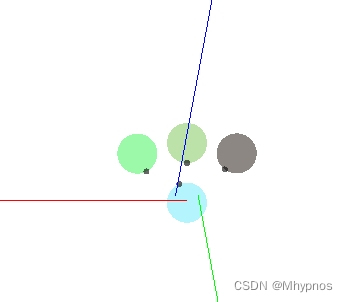
len = 5

len = 10

i半平面直接无转向

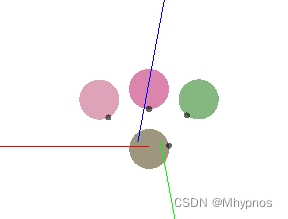
可以看到，不同的参数，物体的避障趋势是不一样的，但是最终都是可以成功避障的

动态效果

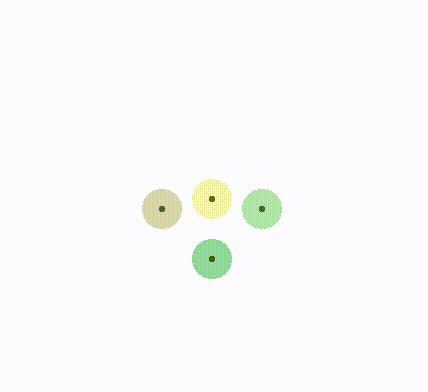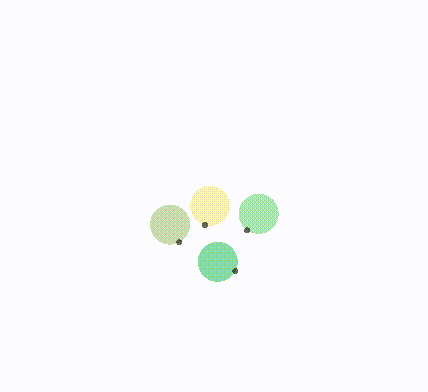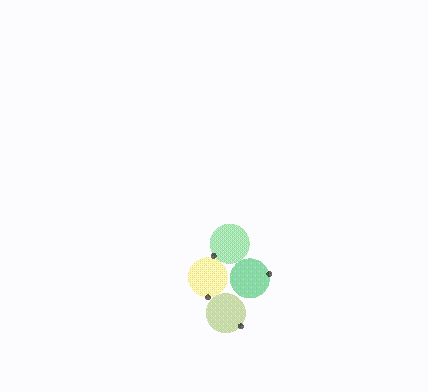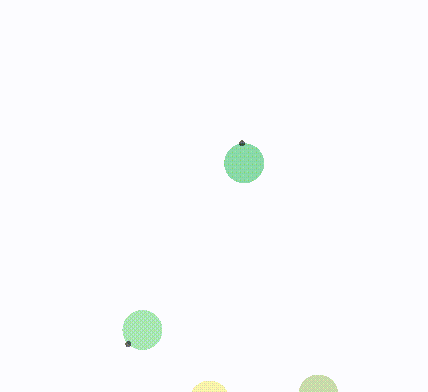
len = 1，旋转1/2夹角

len < 1/2,更趋近于0，i半平面旋转更多

len > 1，更趋近于无穷大，i半平面旋转更少

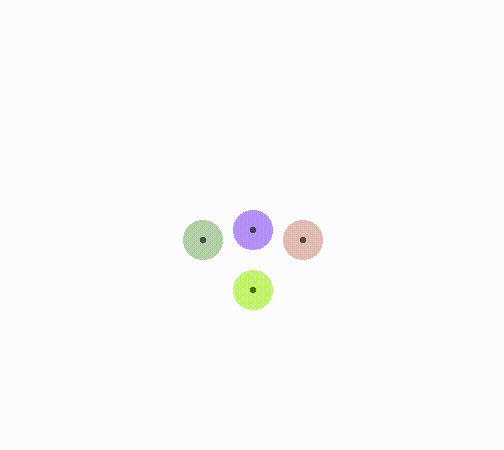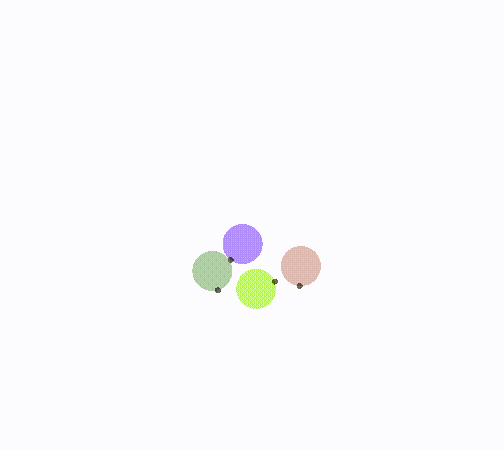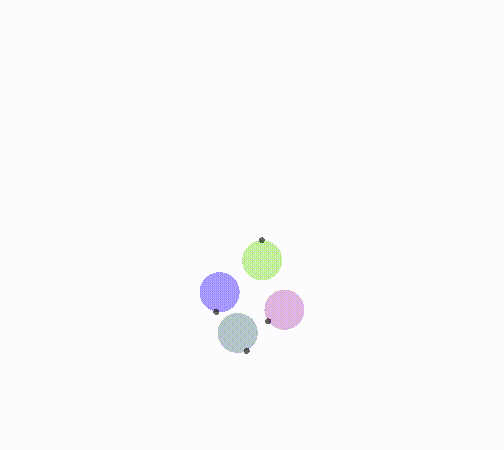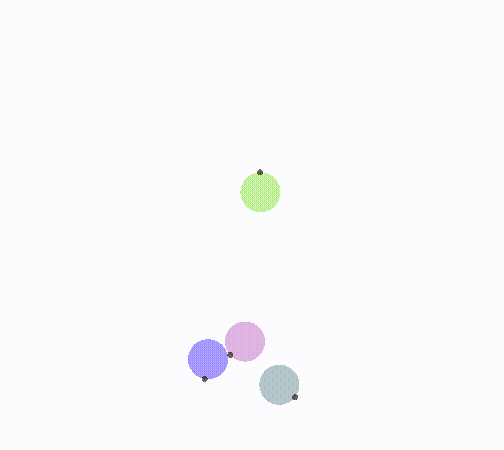
i半平面不转向

大量物体

len = 1，旋转1/2夹角

len < 1/2,更趋近于0，i半平面旋转更多

len > 1，更趋近于无穷大，i半平面旋转更少

i半平面不转向

一些问题

某些情况下，可能会出现物体都静止不动的情况

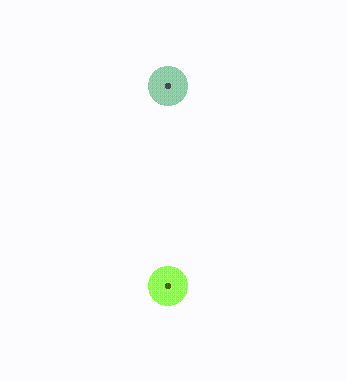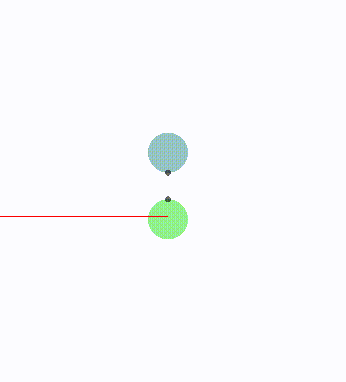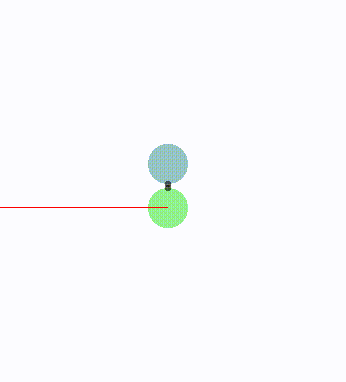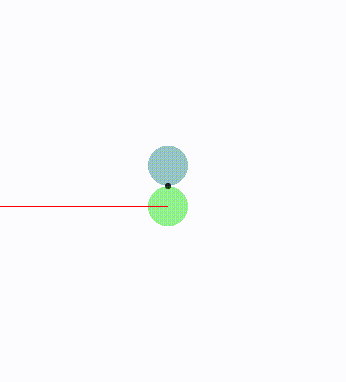
有的时候出现双方，避障权重一样，速度一样，方向相对，位置也是相对。
最后都静止不动了。以上述例子来看，下面的球速度始终是垂直向上，上面的球速度始终是垂直向下。双打的速度始终在碰撞半平面的可行域里，但是为了避免碰撞，双方的速度越来越小

再加上，时间的间隔也非常小

最终由于浮点数计算，导致物体的位置每帧不变

位置，速度都不变，ORCA求的新速度也不变，就导致最终的效果是双方最终都停在原地了

但实际项目中，一般不会有这种情况，因为此时只要一个外来的变化量，或者双方目标速度，权重，啥的有一点点变化。就随便一个微量情况，打破了这种平衡，物体就会继续移动下去。只是可能会出现物体在原地磨蹭了很久之后，才相互错开。因此。具体项目在使用源代码的时候，还需要根据不同需求做不同的调整

这篇关于AI - 碰撞避免算法分析(ORCA)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---