本文主要是介绍[GIS原理] 4.4 镶嵌空间数据结构 - Voronoi图/Thienssen多边形 | Delaunay三角网 | TIN,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 镶嵌式空间数据结构
- DEM
- Voronoi图/Thienssen多边形/Delaunay三角网
- TIN数据结构
镶嵌式空间数据结构
【镶嵌数据模型】用规则或不规则的小面块集合来逼近自然界不规则的地理单元
- 规则镶嵌数据模型:DEM(适合于观测样点均匀分布)
- 不规则镶嵌数据模型:TIN、Voronoi图(适合于不规则有限离散杨店分布)
DEM
Voronoi图/Thienssen多边形/Delaunay三角网
链接
TIN数据结构
【TIN】采用不规则三角网形成对地理空间的完整覆盖
- 在TIN模型中,样点的位置控制着三角形的顶点,这些三角形尽可能接近等边
- TIN能较好地表达地理现象的空间变化,如地形表面就可用三角网拟合,此时三角形看作是空间的三角面片
【优点】
- 充分利用地貌的特征点、线、面,能较好的表示复杂地形
可利用悬崖、断层、海岸线、山谷山脊线等作为约束条件,构造出约束TIN,可以拟合复杂地形 - 根据不同地形,选取合适的采样点数
三角形大小随着点密度的变化而变化,而点密度由地形决定。例如平原地带,地势缓慢,点密度较小,导致三角面片较大 - 进行地形分析和绘制立体图也很方便
【缺点】
- 数据结构复杂,不方便规范化与管理
- 难以与矢量和栅格数据联合分析
【文件组织方式】
-
以三角形为基本对象:点文件(点ID、XY坐标、其他属性列)、三角形拓扑文件(三角形ID、三角形顶点、邻接三角形)

-
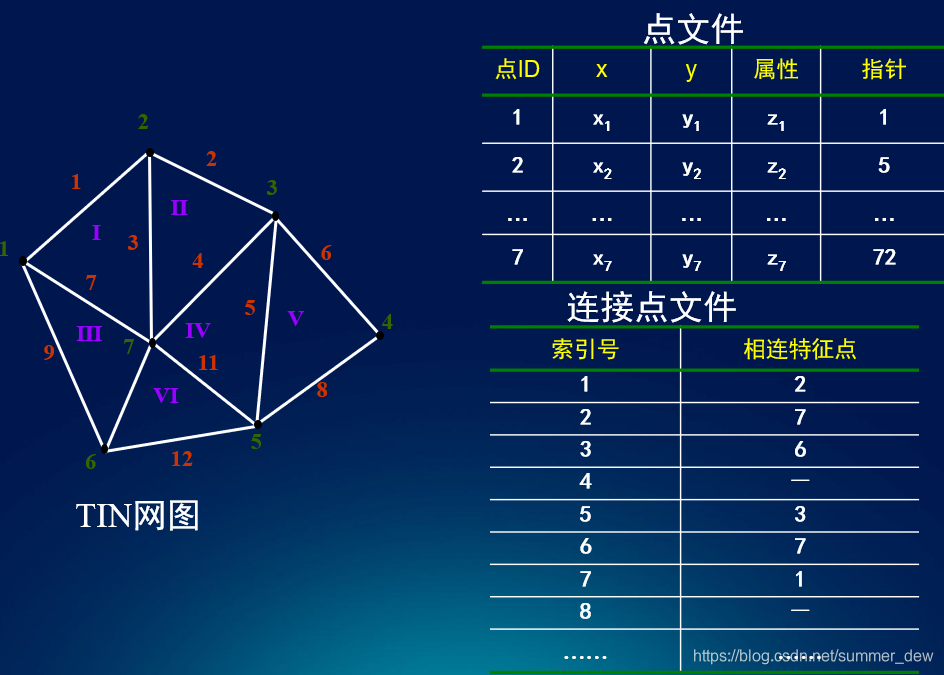
以结点为基本对象
- 点文件:点ID、坐标XY、属性栏、指针(与该点连接的第一个顶点)
- 连接点文件:索引号num、相连特征点next。表示索引号num的下一个结点是next
这篇关于[GIS原理] 4.4 镶嵌空间数据结构 - Voronoi图/Thienssen多边形 | Delaunay三角网 | TIN的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







