voronoi专题

Voronoi 图的增量式构造与归并构造原理

完整内容见 https://dezeming.top/?page_id=973

路径规划算法：Voronoi Planner讲解

路径规划算法：Voronoi Planner讲解附赠自动驾驶学习资料和量产经验：链接 Voronoi Diagram(也称作Dirichlet tessellation)是由俄国数学家Georgy Voronoy提出的一种空间分割算法。它通过一系列的种子节点(Seed Points)将空间切分为许多子区域，每个子区域被称为一个Cell，每个Cell中的所有点到当前Cell中的种子节点(S

shapely 笔记 voronoi图

Voronoi 图是一种将平面分割成区域的方法，每个区域包含一个输入点，任何在该区域内的点都比其他输入点更接近该区域的输入点 1 基本使用方法 shapely.ops.voronoi_diagram(geom, envelope=None, tolerance=0.0, edges=False) 2 参数说明 geom任何几何类型。几何体的所有顶点将被用作 Voronoi 图的输入点edg

[GIS原理] 4.4 镶嵌空间数据结构 - Voronoi图/Thienssen多边形 | Delaunay三角网 | TIN

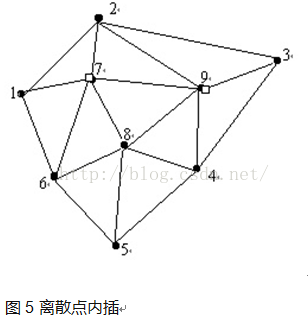
文章目录镶嵌式空间数据结构DEMVoronoi图/Thienssen多边形/Delaunay三角网TIN数据结构镶嵌式空间数据结构【镶嵌数据模型】用规则或不规则的小面块集合来逼近自然界不规则的地理单元规则镶嵌数据模型：DEM（适合于观测样点均匀分布）不规则镶嵌数据模型：TIN、Voronoi图（适合于不规则有限离散杨店分布） DEM Voronoi图/Thiens

沃罗诺伊图（Voronoi Diagram，也称作Dirichlet tessellation，狄利克雷镶嵌）

沃罗诺伊图（Voronoi Diagram，也称作Dirichlet tessellation，狄利克雷镶嵌）是由俄国数学家格奥尔吉·沃罗诺伊建立的空间分割算法。灵感来源于笛卡尔用凸域分割空间的思想。在几何，晶体学建筑学，地理学，气象学，信息系统等许多领域有广泛的应用。泰森多边形法，荷兰气候学家A·H·Thiessen提出了一种根据离散分布的气象站的降雨量，来计算平均降雨量的方法，即将所有相邻

沃罗诺伊图——Voronoi Partition 可汗学院

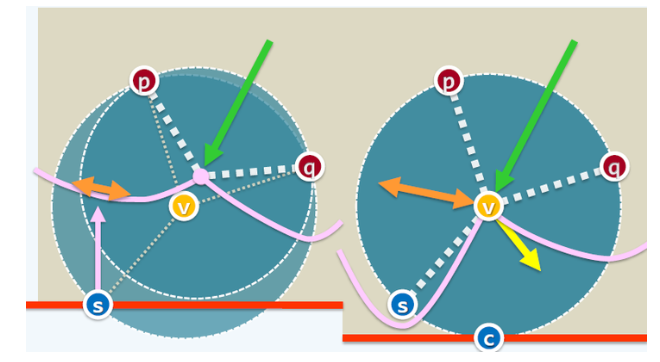
看到一个非常棒的解释 Voronoi Diagram 的视频，给大家搬运过来！先说说两个圆的情况：不停放大半径，直至相交，出现边。再说说多个圆的情况：放大相交得：然后一起了解一下术语：再说说性质： 1. 每一条边到最近的两个site的距离相等： 2. 每条边相交的点到最近的三个site距离相等：

Delaunay三角网与Voronoi图

原文地址：Delaunay三角网与Voronoi图作者：jenny (实线多边形就是Delaunay三角网；虚线多边形式Voronoi图) 　　Voronoi图，又叫泰森多边形或Dirichlet图，它是由一组由连接两邻点直线的垂直平分线组成的连续多边形组成。N个在平面上有区别的点，按照最邻近原则划分平面；每个点与它的最近邻区域相关联。Delaunay三角形是由与相邻Voro

voronoi图的和Delaunay三角剖分

看了几个关于voronoi图的和Delaunay三角剖分的介绍，按照自己的理解综合大家的想法。总结一下这两个的知识。 Voronoi图定义： Voronoi图:计算几何里的一种基于距离的平面划分方法。在平面上有n个不重合种子点（节点），把平面分为n个区域，使得每个区域内的点到它所在区域的种子点（节点）的距离比到其它区域种子点（节点）的距离近。每个区域称为该种子点（节点）的Voronoi区域。V

delaunay和voronoi图人脸三角剖分

先获取人脸68个特征点坐标，其中使用了官方的预训练模型shape_predictor_68_face_landmarks.dat： import dlibimport cv2predictor_path = "shape_predictor_68_face_landmarks.dat"png_path = "face.jpg"txt_path = "points.txt"f = open(

delaunay和voronoi图人脸三角剖分

先获取人脸68个特征点坐标，其中使用了官方的预训练模型shape_predictor_68_face_landmarks.dat： import dlibimport cv2predictor_path = "shape_predictor_68_face_landmarks.dat"png_path = "face.jpg"txt_path = "points.txt"f = open(

matlab中绘制维诺图（Voronoi Diagram）

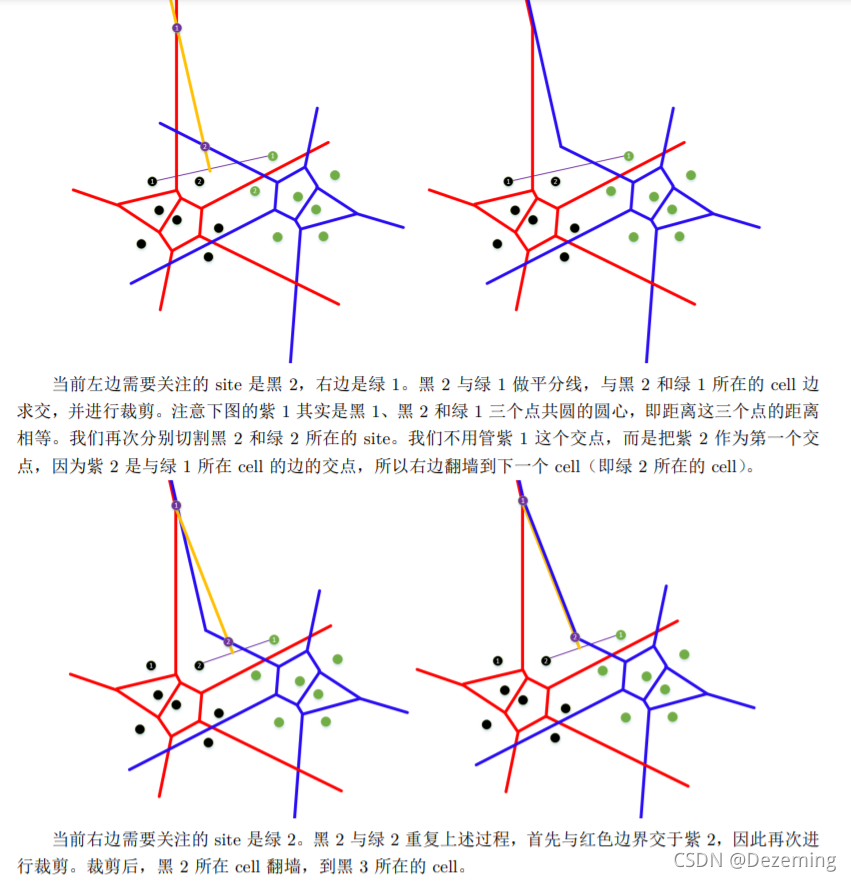
1.专业术语（相关概念）：基点Site：具有一些几何意义的点细胞Cell：这个Cell中的任何一个点到Cell中基点中的距离都是最近的，离其他Site比离内部Site的距离都要远。 Cell的划分：基点Site与其它的n-1个点所对应的那个平分线所确定的那个离它更近的那个半平面。把所有这些半平面公共的交集求出来就是这个cell. 因此每个Cell都是凸的，图中一定会有一些Cell是无界的

沃罗诺伊图（Voronoi）：迷人的世界【1/2】

一、说明 Voronoi图（也称为狄利克雷镶嵌或泰森多边形）在自然界中无处不在。你已经遇到过他们数千次了，但也许没有这样称呼它。Voronoi图很简单，但它们具有令人难以置信的特性，在制图，生物学，计算机科学，统计学，考古学，一直到建筑和艺术等领域都有应用。二、什么是沃罗诺伊图？假设您有 n 个点分散在一个平面上，这些点的 Voron

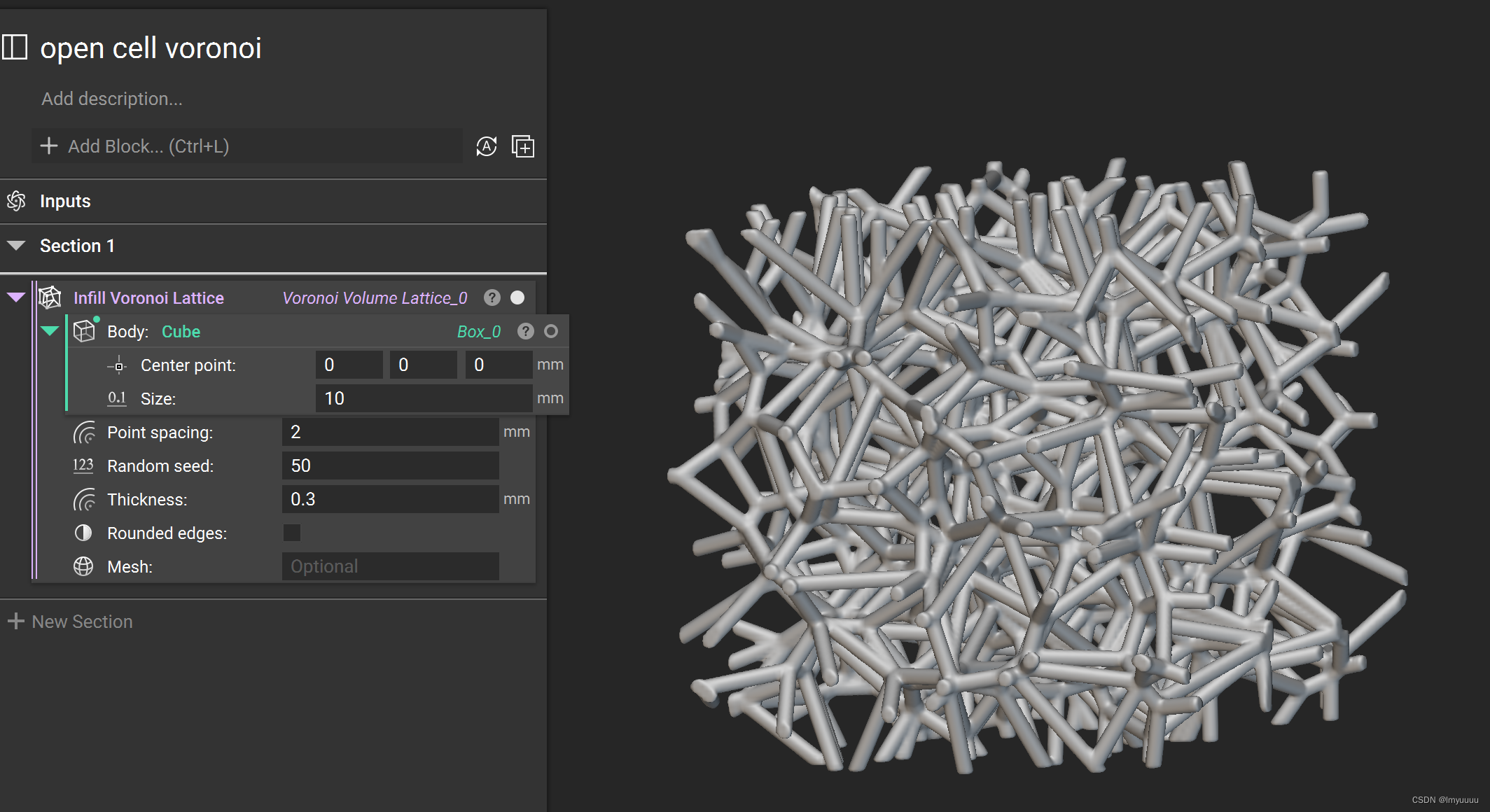
【开源】开孔泡沫结构建模/voronoi泡沫/voronoi晶体/多胞材料/维诺结构/泰森多边形

注：开源分享，任何人不得将其打包对外出售等，遵从GPL协议，若在此基础上做了修改，那么修改后的代码/文章也必须开源。目录注：开源分享，任何人不得将其打包对外出售等，遵从GPL协议，若在此基础上做了修改，那么修改后的代码/文章也必须开源。一、概念二、建模 2.1 voronoi晶体 2.2 二维voronoi泡沫 2.3 三维开孔泡沫三、其他一、概念