Delaunay三角网与Voronoi图

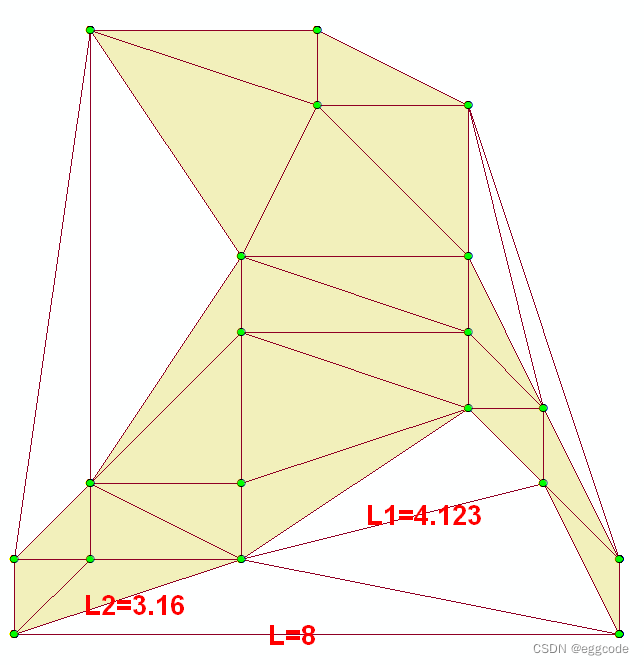
(实线多边形就是Delaunay三角网；虚线多边形式Voronoi图)

　　Voronoi图，又叫泰森多边形或Dirichlet图，它是由一组由连接两邻点直线的垂直平分线组成的连续多边形组成。N个在平面上有区别的点，按照最邻近原则划分平面；每个点与它的最近邻区域相关联。Delaunay三角形是由与相邻Voronoi多边形共享一条边的相关点连接而成的三角形。Delaunay三角形的外接圆圆心是与三角形相关的Voronoi多边形的一个顶点。Voronoi三角形是Delaunay图的偶图；

　　对于给定的初始点集P，有多种三角网剖分方式，其中Delaunay三角网具有以下特征：

　　1、Delaunay三角网是唯一的；

　　2、三角网的外边界构成了点集P的凸多边形“外壳”；

　　3、没有任何点在三角形的外接圆内部，反之，如果一个三角网满足此条件，那么它就是Delaunay三角网。

　　4、如果将三角网中的每个三角形的最小角进行升序排列，则Delaunay三角网的排列得到的数值最大，从这个意义上讲，Delaunay三角网是“最接近于规则化的“的三角网。

　　Delaunay三角形网的特征又可以表达为以下特性：

　　1、在Delaunay三角形网中任一三角形的外接圆范围内不会有其它点存在并与其通视，即空圆特性；

　　2、在构网时，总是选择最邻近的点形成三角形并且不与约束线段相交；

　　3、形成的三角形网总是具有最优的形状特征，任意两个相邻三角形形成的凸四边形的对角线如果可以互换的话，那么两个三角形6个内角中最小的角度不会变大；

　　4、不论从区域何处开始构网，最终都将得到一致的结果，即构网具有唯一性。

　　Delaunay三角形产生的基本准则：任何一个Delaunay三角形的外接圆的内部不能包含其他任何点[Delaunay 1934]。Lawson[1972]提出了最大化最小角原则，每两个相邻的三角形构成凸四边形的对角线，在相互交换后，六个内角的最小角不再增大。Lawson[1977提出了一个局部优化过程（LOP, local Optimization Procedure）方法。