三角网专题

MATLAB 地面点构建三角网（83）

MATLAB 地面点构建三角网（83）一、算法介绍二、算法实现1.代码一、算法介绍使用少量的抽稀后的地面点。构建了一层2.5维的三角网，用于表示地形的起伏变化，随着点数量增多，构建和耗时都会相应增加，这里只是输出和研究三角网构建效果，并不做实际工程使用，具体的构建结果和代码如下，直接复制粘贴使用即可二、算法实现 1.代码代码如下（示例）： % 从 PLY 文

Civil 3d中三角网曲面求取二维和三维面积

直接来点源码： public void CreateTinSurfaceArea() { try { string strErr = ""; ObjectId sId = PromptOptionsHelper.GetPromptEntOptions("请选择曲面",

【NetTopologySuite类库】C#生成Delaunay三角网、生成凹包ConcaveHull

介绍三角网生成三角网的API地址：https://nettopologysuite.github.io/NetTopologySuite/api/NetTopologySuite.Triangulate.ConformingDelaunayTriangulationBuilder.html#methods 凹包生成凹包的API地址： https://nettopologysuite.

【NetTopologySuite类库】C#生成带约束（线、面）的Delaunay三角网

介绍 API地址：https://nettopologysuite.github.io/NetTopologySuite/api/NetTopologySuite.Triangulate.ConformingDelaunayTriangulationBuilder.html#NetTopologySuite_Triangulate_ConformingDelaunayTriangulationB

threejs 根据离散点生成不规则三角网（三角剖分），检测点是否在该三角网内（区域搜索）

我们知道threejs中的模型都是一个个三角网组成的，三角网数量越多，模型就越精细。在 Three.js 中，你可以通过创建一个三角网格对象来表示三维模型，这个对象通常由一个顶点数组和一个索引数组构成。顶点数组包含了模型的各个顶点的坐标信息，而索引数组则定义了如何将这些顶点连接起来形成三角形。通过修改这些顶点的坐标信息，你可以改变模型的形状，从而实现各种各样的动

利用C#生成一个简单的TIN三角网

###输入TXT数据 private void inputbutton_Click(object sender, EventArgs e){OpenFileDialog opg = new OpenFileDialog();opg.Title = "选择文本数据";opg.Filter = "Txt数据(*.txt)|*.txt";opg.ShowDialog();strName = opg.F

【读论文】2019-基于三角网滤波和支持向量机的点云分类算法

摘要提出一种基于渐进加密三角网和双层支持向量机的点云分类算法采用渐进加密三角网滤波提取地面，在地物点的基础上对地物点进行归一化处理。对点云特征进行评估，选取特征向量并用最近邻支持向量机（NN-SVM）对地物点进行分类。创新点基于NN-SVM提出一种将分类分为粗细双层的分类策略。其中粗分类过程为：提取特征，对特征进行选择（使用libsvm的F-score模块)，选择有效性高的特征，

[GIS原理] 9 数字地形分析DTA、数字地形模型DTM、数字高程模型DEM、数字地表模型DSM、不规则三角网TIN

在知识传播途中，向涉及到的相关著作权人谨致谢意！文章目录 1 数字地形分析（DTA）1.1 数字地形模型（DTM）1.1.1 DSM与DEM对比 1.2 数字地形分析研究与应用进展1.2.1 DEM模型的拓展1.2.1.1 高保真数字高程模型1.2.1.2 平原河网区P-DEM构建 1.2.2 DEM表达方式的拓展1.2.3 DEM地形分析方法的进展1.2.3.1 基于DEM的地形

[GIS原理] 4.4 镶嵌空间数据结构 - Voronoi图/Thienssen多边形 | Delaunay三角网 | TIN

文章目录镶嵌式空间数据结构DEMVoronoi图/Thienssen多边形/Delaunay三角网TIN数据结构镶嵌式空间数据结构【镶嵌数据模型】用规则或不规则的小面块集合来逼近自然界不规则的地理单元规则镶嵌数据模型：DEM（适合于观测样点均匀分布）不规则镶嵌数据模型：TIN、Voronoi图（适合于不规则有限离散杨店分布） DEM Voronoi图/Thiens

CGAL 获取一个面的所有边（三角网）

文章目录一、简介二、实现代码三、实现效果参考资料一、简介由于CGAL中的三角网是基于顶点+面片为基础进行构建的，因此每个面片的边都是隐式表示的，即顶点和面片的相对关系。二、实现代码一个小实验，获取一条边： #include <iostream>#include <vector>#

CGAL 过滤三角网算法求取凹包面积

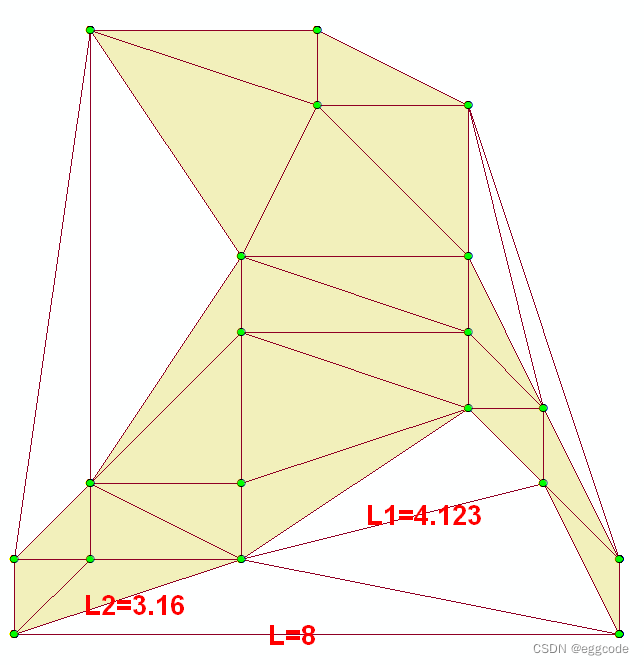
文章目录一、简介二、实现代码三、实现效果参考资料一、简介该方法是复现了论文中的方法，主要思想是：（1）首先需要构建二维点云的三角网，在此基础上我们来剔除点云边界可能存在的空隙，这里我们需要指定一个边长阈值。（2）根据阈值剔除掉外部间隙。若要剔除点云数据边界的外部间隙，需设定最外层三角形过滤阈值。当外部三角形边长超过阈值时，则认为此三角形是外部空隙进而剔除。当外部三

Delaunay三角网与Voronoi图

原文地址：Delaunay三角网与Voronoi图作者：jenny (实线多边形就是Delaunay三角网；虚线多边形式Voronoi图) 　　Voronoi图，又叫泰森多边形或Dirichlet图，它是由一组由连接两邻点直线的垂直平分线组成的连续多边形组成。N个在平面上有区别的点，按照最邻近原则划分平面；每个点与它的最近邻区域相关联。Delaunay三角形是由与相邻Voro

使用等高线和特征点创建TIN（不规则三角网）的方法

这里演示一下如何通过等高线和特征点来创建TIN（不规则三角网）这里使用的是不规则采样点建立DEM的点数据还差等高线，通过新建线要素-添加Height字段并赋给它高程值来得到找到工具，3D Analyst工具-数据管理-创建TIN，双击按下图所示设置参数其中，高度字段都是带有高程值的height字段，散点数据的SF Type为Mass_Points，等高线数据的SF Type为S

CGAL 三角网删除面片

文章目录一、简介二、实现代码三、实现效果参考资料一、简介在CGAL中，删除一个面片要比删除一个顶点容易很多，它的时间复杂度是O(1)，所以删除的效率也很快，不过在删除的过程中其附属的边结构会遭到破坏，因此这个操作可能对某些具有顺序的算法有所用处。具体的效果如下所示。二、实现代码 #include <iostream>#include <vector>#<

matlab中构建三角网,MATLAB绘制三角网及三维网线

今天博主给大家介绍一些比较常见的可视化操作，绘制三角网及三维网线。三角网是由一系列连续三角形构成的网状的平面控制图形，是三角测量中布设连续三角形的两种主要扩展形式，同时向各方向扩展而构成网状，优点为点位分布均匀、各点之间互相牵制、图形强度较高，缺点是扩展较缓慢。三角网是实现地形三维可视化，数字地面模型(Digital Terrain Model，简称DTM)是一种很有效的途径。DTM主要是由

matlab中构建三角网,MATLAB绘制三角网及三维网线

今天博主给大家介绍一些比较常见的可视化操作，绘制三角网及三维网线。三角网是由一系列连续三角形构成的网状的平面控制图形，是三角测量中布设连续三角形的两种主要扩展形式，同时向各方向扩展而构成网状，优点为点位分布均匀、各点之间互相牵制、图形强度较高，缺点是扩展较缓慢。三角网是实现地形三维可视化，数字地面模型(Digital Terrain Model，简称DTM)是一种很有效的途径。DTM主要是由

matlab 不规则三角网,[转载]不规则三角网(TIN)生成等高线的算法

根据离散点的三维坐标生成等高线的方法主要有网格法和三角网法。三角网方法相比与网格法，能够用较少的空间和时间更精确的拟合复杂地表面，因而得到了广泛的应用。本文主要介绍三角网法生成等高线的算法。下一篇文章用代码实现。 1. 构造狄洛尼三角在狄洛尼法中将离散分布的地形点称为“参考点”。构成狄洛尼三角网时规定：“每个参考点组成的三角形的外接圆都不包含其他参考点”。其计算方法如下： 1)任取一个参考点作

matlab 不规则三角网,[转载]不规则三角网(TIN)生成等高线的算法

根据离散点的三维坐标生成等高线的方法主要有网格法和三角网法。三角网方法相比与网格法，能够用较少的空间和时间更精确的拟合复杂地表面，因而得到了广泛的应用。本文主要介绍三角网法生成等高线的算法。下一篇文章用代码实现。 1. 构造狄洛尼三角在狄洛尼法中将离散分布的地形点称为“参考点”。构成狄洛尼三角网时规定：“每个参考点组成的三角形的外接圆都不包含其他参考点”。其计算方法如下： 1)任取一个参考点作