【开源】开孔泡沫结构建模/voronoi泡沫/voronoi晶体/多胞材料/维诺结构/泰森多边形

注：开源分享，任何人不得将其打包对外出售等，遵从GPL协议，若在此基础上做了修改，那么修改后的代码/文章也必须开源。

目录

注：开源分享，任何人不得将其打包对外出售等，遵从GPL协议，若在此基础上做了修改，那么修改后的代码/文章也必须开源。

一、概念

二、建模

2.1 voronoi晶体

2.2 二维voronoi泡沫

2.3 三维开孔泡沫

三、其他

一、概念

开孔泡沫是一种具有许多开放孔隙的材料结构，通常由连续的固态结构和分散的气泡组成。这种结构使得开孔泡沫具有轻质、吸音、隔热和吸能等特性。

多胞材料(Cellular materials)是指用固体棱边或者固体壁面所构成的孔穴组合体，其内部含有大量空穴又具有一定胞结构，相对密度一般小于0.3， 即孔隙率大于0.7。

Voronoi图，也称为狄利克雷镶嵌或泰森多边形，在自然界中无处不在，Voronoi 图是一种细分模式，其中分散在平面上的许多点细分为正好 n 个单元格，包围着最接近每个点的平面部分。（ref：沃罗诺伊图的迷人世界 |内置 (builtin.com)）

关于Voronoi图的生成原理，想象你在一个沙漠里，而有两口井可以取水。如果你想去最近的井，应该去哪口井？显然，这取决于你站立的位置。可以画一条划分沙漠的线：在线路的“左边”，去“左边”的井上更近，在线的“右边”，去“右边”的井更近。 这条线实际上就是两口井之间的中垂线，那么现在有第三口井、第四口井..那么你可以继续进行划分，于是可以得到距离每个井更近的空间。（ref：沃罗诺伊镶嵌 (datagenetics.com)  强烈推荐初学者仔细看看这篇BLOG，非常生动形象通俗易懂）：

Voronoi 图是一种将空间划分为不重叠的区域的方法，其中每个区域都由一个中心点和与该中心点最近的其他点组成。在开孔泡沫建模中，Voronoi 算法可以用于生成具有随机或规则分布的泡沫结构。  Laguerre tessellation（待补全）

二、建模

生成泰森多边形结构的方式有很多种，这里主要讨论voronoi算法生成。

目前主流的建模方法分为MATLAB/PYTHON两种，但我在此分享的仅仅为其他更简单的构建方法，相对于刚开始接触此领域但没有传承的同学来说更容易上手。

2.1 voronoi晶体

已经有了非常成熟的开源，但没有那么好上手：

①NEPER

请参照Neper: Polycrystal Generation and Meshing — Neper 4.6.1 documentation

Neper是一个需要在linux环境下利用python生成晶体模型的开源软件包，因此为了成功使用，需要学习linux常见调用命令、熟练安装各种依赖/组件、认真学习neper帮助文档。以及查阅 Pavel Ferkl. Mathematical Modelling of Properties and Evolution of Polymer Foams. PhD thesis, University of Chemistry and Technology Prague, 2018.

如果你是完全不懂这些的新手，我更建议考虑在linux下安装conda，再用conda安装neper，在github上可以找到快捷指令。

ps：安装linux系统，Win10 (1809 以上) 的用户可以通过终端直接使用 Linux ubuntu 子系统 (WSL)，但没有可视化界面也就意味着对命令使用要求更高，建议按照自己的情况分别处理，win11界面进入linux系统如下：

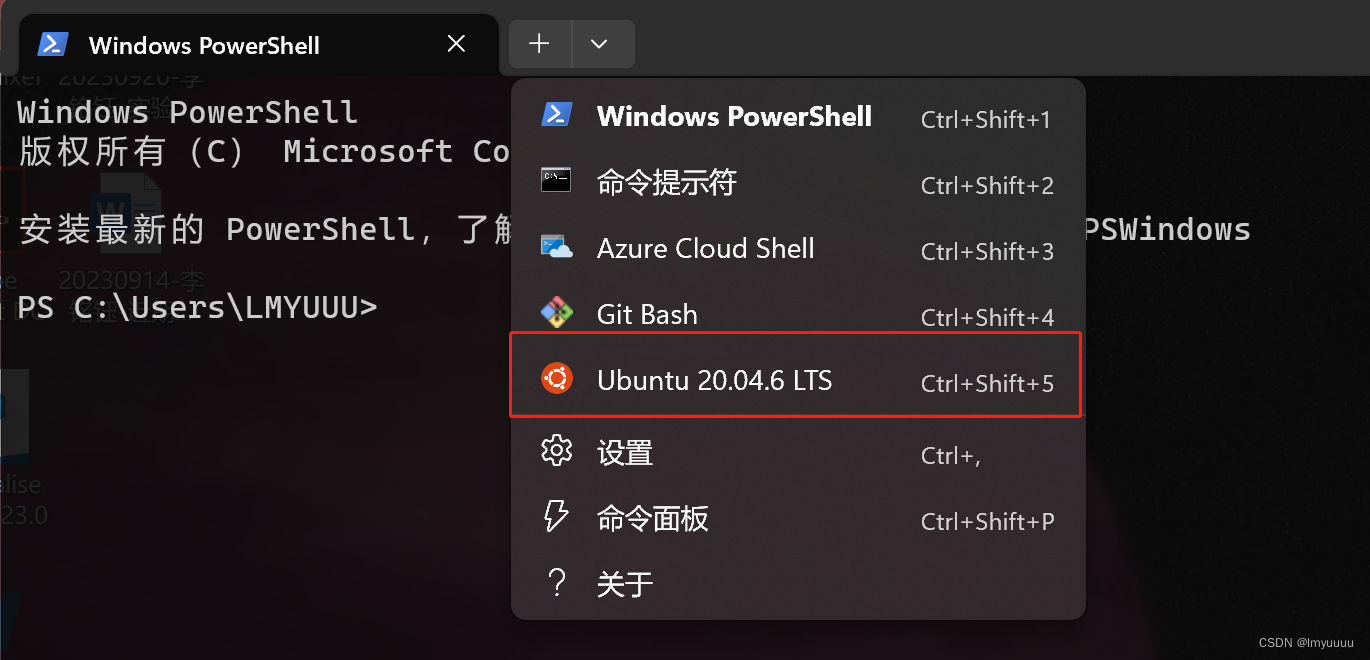
对于命令调用，我常用的基本命令只有下面几个：

1. ls：列出当前目录下的文件和子目录。

2. pwd：显示当前工作目录的路径。

3. cd：切换目录。例如，cd /path/to/directory 可以进入指定目录。

4. mkdir：创建新目录。使用方式如下：mkdir new_directory。

5. rmdir：删除空目录。例如，rmdir empty_directory。

6. cp：复制文件或目录。例如，cp file1 file2 会将file1复制到file2。

7. mv：移动文件或重命名文件。可以用它来移动文件或目录，也可以将文件重命名。例如，mv file1 file2 会将file1重命名为file2。

8. rm：删除文件或目录。请小心使用，因为删除后无法恢复。rm filename 或 rm -r directory（递归删除目录及其内容）。

其他基础学习参照 
Neper 学习文档 | Wiidu
   其他我有空再续写...github上有非常多相关内容，搜一搜可以学会的!

成功运行生成模型如下：

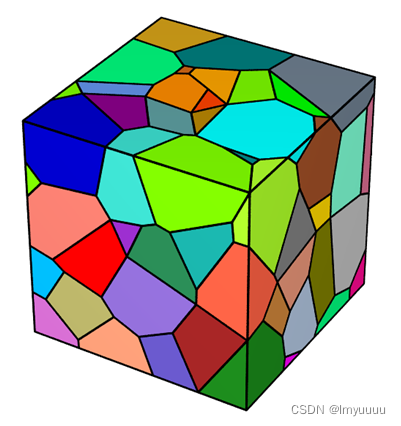
②PYTHON

Abaqus三维多晶体脚本建模-Voronoi多面体建模 (qq.com)

2.2 二维voronoi泡沫

HOMTOOLS - Homogeneization toolbox for Abaqus (cnrs-mrs.fr)

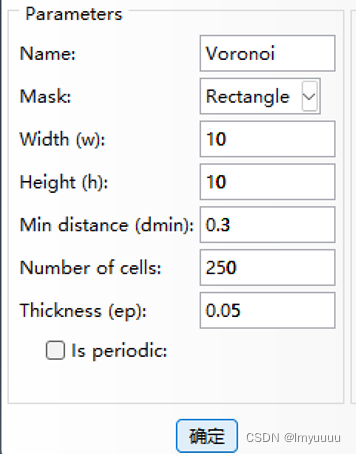
2.3 三维开孔泡沫

其实有很多方式，python或者matlab都可以，但是没有时间慢慢写了，这里我介绍最简单的一种：用软件直接生成。

下载：https://www.huajclub.com/9650.html

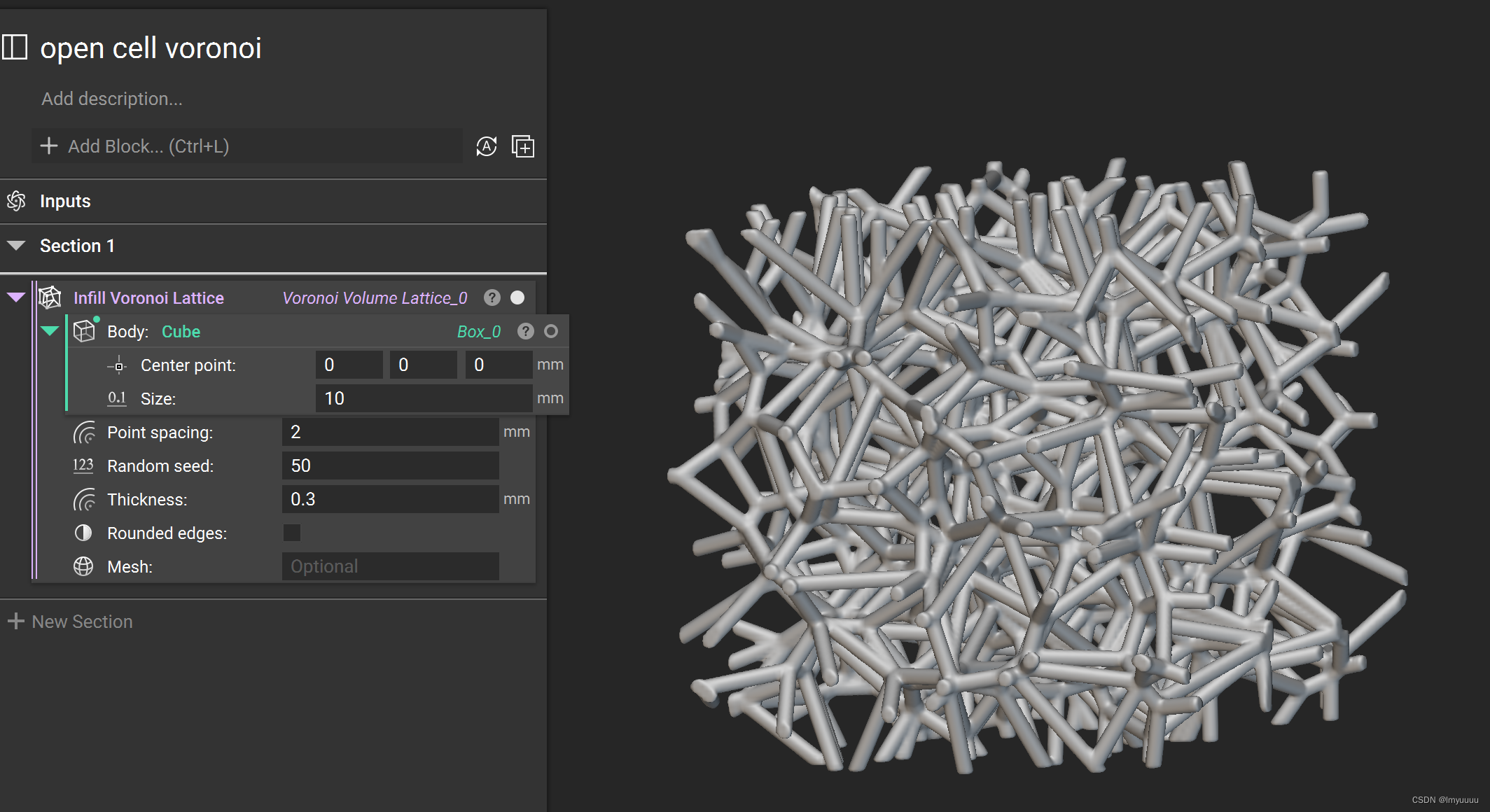
软件逻辑非常简单，就是把内置代码可视化，相当于一键参数化建模，具体可以在他们官网找到很多案例，除了泡沫还有其他模型生成也非常简单，但是需要科学上网。Voronoi lattice ramping thickness and spacing | nTop | nTop

此源文件放在我的资源中。

三、其他

科研不易，希望大家秉承开放、自由的心态交流。

实在太忙，很多地方来不及细写，等我论文完成再来详细写完。

不许拿去别的地方收费!!!!!!!!!