文心一言 VS 讯飞星火 VS chatgpt （193）-- 算法导论14.3 1题

2024-02-04 06:28
文章标签 chatgpt 算法 ai vs 14.3 193 文心一言 讯飞星火 导论

本文主要是介绍文心一言 VS 讯飞星火 VS chatgpt （193）-- 算法导论14.3 1题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、用go语言，写出作用于区间树的结点且在 〇(1) 时间内更新 max 属性的过程 LEFT-ROTATE 的伪代码。

文心一言：

以下是一个简单的LEFT-ROTATE的伪代码，它对一个二叉搜索树进行左旋转操作。这个操作的作用是更新节点的max属性，使其在O(1)时间内完成。

LEFT-ROTATE(T, x):  // T 是树，x 是需要左旋转的节点  y := x.right  x.right := y.left  y.left = x  T.root = y
LEFT-ROTATE的伪代码解释：

首先，记录需要左旋转的节点x的右子节点为y。
然后，将节点x的右子节点指向y的左子节点。
接着，将节点y的左子节点指向节点x。
最后，将整个树T的根节点指向节点y，完成左旋转操作。

在这里插入图片描述

讯飞星火：

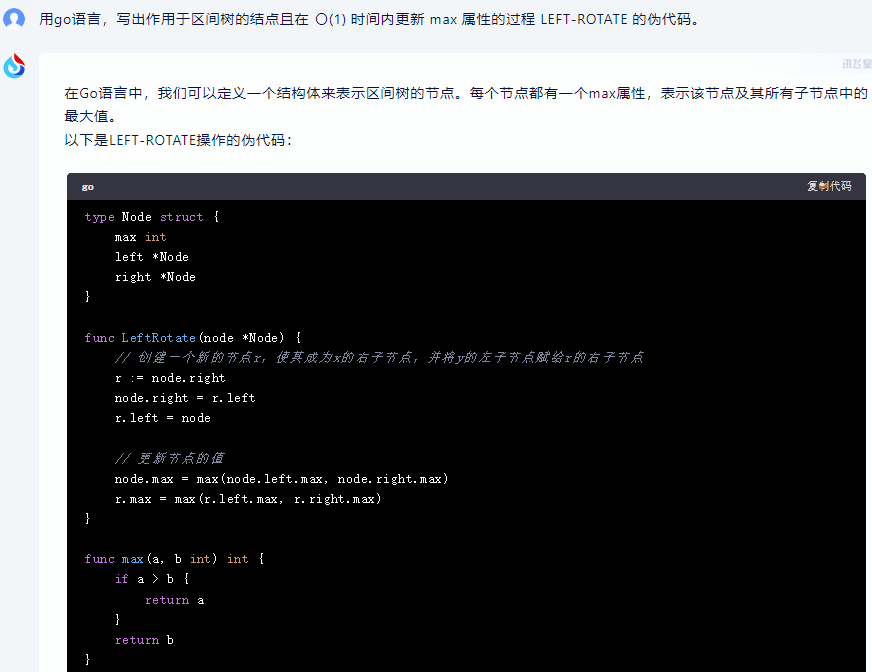
在Go语言中，我们可以定义一个结构体来表示区间树的节点。每个节点都有一个max属性，表示该节点及其所有子节点中的最大值。

以下是LEFT-ROTATE操作的伪代码：

type Node struct {max intleft *Noderight *Node
}func LeftRotate(node *Node) {// 创建一个新的节点r，使其成为x的右子节点，并将y的左子节点赋给r的右子节点r := node.rightnode.right = r.leftr.left = node// 更新节点的值node.max = max(node.left.max, node.right.max)r.max = max(r.left.max, r.right.max)
}func max(a, b int) int {if a > b {return a}return b
}

在这个伪代码中，我们首先将节点的右子节点保存在变量r中，然后将r的左子节点设置为节点的右子节点。然后我们将节点设置为r的左子节点。最后，我们更新节点和r的max属性。

在这里插入图片描述

在这里插入图片描述

360智脑：

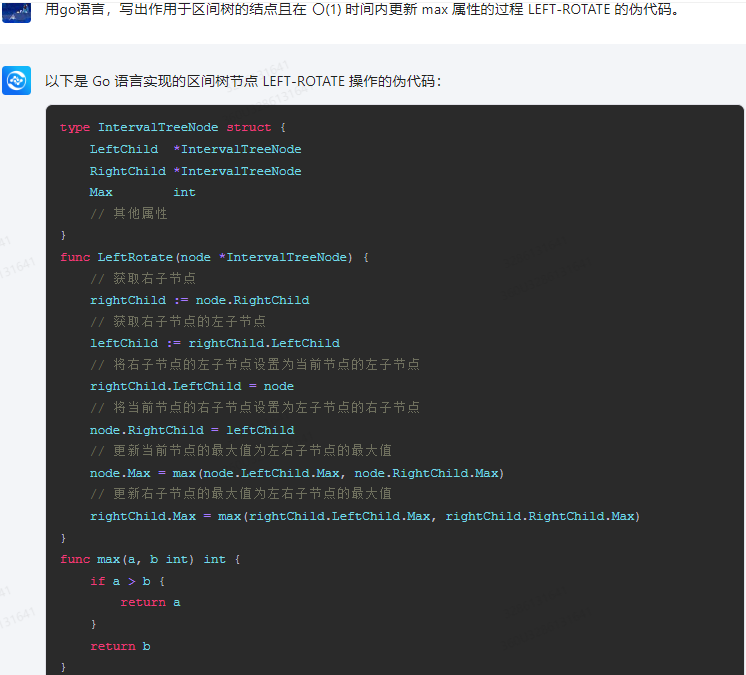
以下是 Go 语言实现的区间树节点 LEFT-ROTATE 操作的伪代码：

type IntervalTreeNode struct {LeftChild  *IntervalTreeNodeRightChild *IntervalTreeNodeMax        int// 其他属性
}
func LeftRotate(node *IntervalTreeNode) {// 获取右子节点rightChild := node.RightChild// 获取右子节点的左子节点leftChild := rightChild.LeftChild// 将右子节点的左子节点设置为当前节点的左子节点rightChild.LeftChild = node// 将当前节点的右子节点设置为左子节点的右子节点node.RightChild = leftChild// 更新当前节点的最大值为左右子节点的最大值node.Max = max(node.LeftChild.Max, node.RightChild.Max)// 更新右子节点的最大值为左右子节点的最大值rightChild.Max = max(rightChild.LeftChild.Max, rightChild.RightChild.Max)
}
func max(a, b int) int {if a > b {return a}return b
}

注意，以上代码仅为示例，具体实现可能需要根据实际需求进行调整。

在这里插入图片描述

在这里插入图片描述

智谱清言：

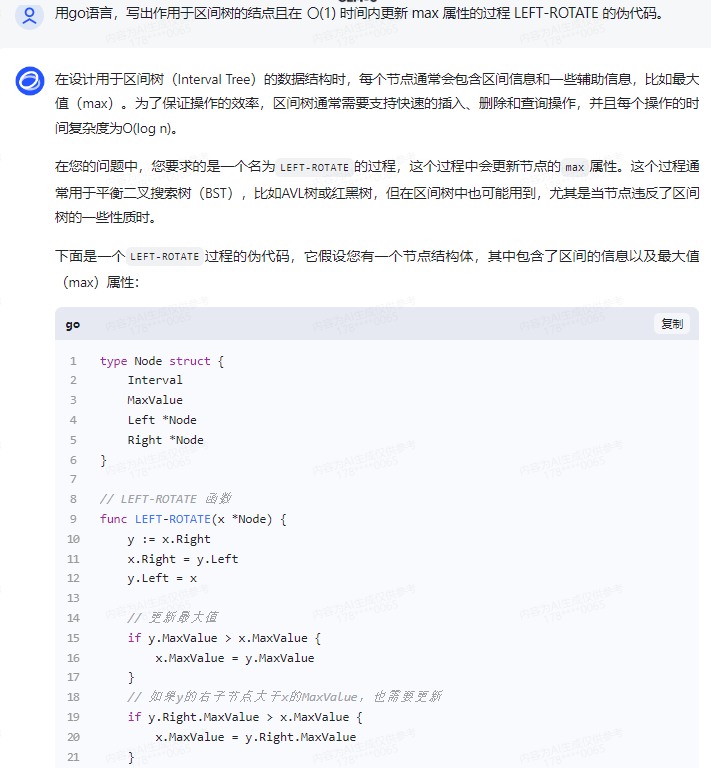
在设计用于区间树（Interval Tree）的数据结构时，每个节点通常会包含区间信息和一些辅助信息，比如最大值（max）。为了保证操作的效率，区间树通常需要支持快速的插入、删除和查询操作，并且每个操作的时间复杂度为O(log n)。

在您的问题中，您要求的是一个名为LEFT-ROTATE的过程，这个过程中会更新节点的max属性。这个过程通常用于平衡二叉搜索树（BST），比如AVL树或红黑树，但在区间树中也可能用到，尤其是当节点违反了区间树的一些性质时。

下面是一个LEFT-ROTATE过程的伪代码，它假设您有一个节点结构体，其中包含了区间的信息以及最大值（max）属性：

type Node struct {IntervalMaxValueLeft *NodeRight *Node
}
// LEFT-ROTATE 函数
func LEFT-ROTATE(x *Node) {y := x.Rightx.Right = y.Lefty.Left = x// 更新最大值if y.MaxValue > x.MaxValue {x.MaxValue = y.MaxValue}// 如果y的右子节点大于x的MaxValue，也需要更新if y.Right.MaxValue > x.MaxValue {x.MaxValue = y.Right.MaxValue}// 返回新的根节点return y
}

在这个伪代码中：

  • Interval 表示节点包含的区间类型。

  • MaxValue 是节点上的最大值属性。

  • Left 和 Right 是指向节点左子树和右子树的指针。

LEFT-ROTATE函数会交换x节点和它的右子节点y，并更新指针。在交换之后，x会成为y的右子节点，而y原来的右子节点成为了x的左子节点。

更新x的MaxValue属性是一个关键步骤，确保在旋转后max属性仍然是正确的。这需要比较x的MaxValue和y以及y的右子节点的MaxValue，取三者中的最大值作为x的新MaxValue。

请注意，这段伪代码是通用的，并且没有考虑具体的实现细节，比如Interval类型的定义，或者节点如何具体地存储和管理区间。在实际应用中，您可能需要根据您的具体需求对这段代码进行调整。

在这里插入图片描述

在这里插入图片描述

通义千问：

区间树（Interval Tree）和二叉搜索树（BST）不同，它的节点通常包含一个区间而不是单个值，并且设计时会维护一些附加属性来支持高效的区间查询。然而，对于区间树来说，没有直接对应的LEFT-ROTATE操作，因为旋转操作主要是在调整二叉搜索树的平衡时使用的，如在AVL树或红黑树中。

如果你的区间树实现了一个基于BST的结构，并且确实有一个max属性表示每个节点所代表区间范围的最大值，同时假设每次插入或删除区间后都需要更新相关节点及其祖先的最大值属性，那么在进行旋转操作时，必须确保max属性的正确性。

下面是一个简化的LEFT-ROTATE操作伪代码，它适用于任何类型的BST节点，包括可能存储区间的节点。在旋转过程中，我们会确保重新计算父节点和新旋转后子节点的最大值属性：

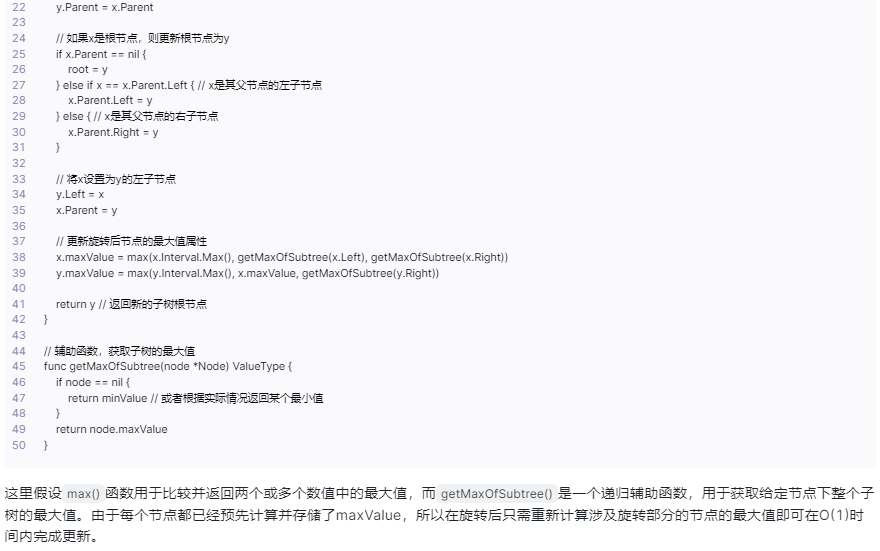
// 定义区间树节点结构，其中包含了最大值属性
Node {Interval interval; // 区间对象MaxValue maxValue; // 节点所涵盖的最大值Left, Right *Node; // 左右子节点指针
}// 左旋操作，以x为旋转轴心节点
func leftRotate(x *Node) *Node {// 获取x的右子节点作为新的根节点y := x.Right// x原来的右子节点的左子节点成为x的新右子节点x.Right = y.Left// 如果y的左子节点非空，则其父节点改为xif y.Left != nil {y.Left.Parent = x}// 更新y的父节点为x的父节点y.Parent = x.Parent// 如果x是根节点，则更新根节点为yif x.Parent == nil {root = y} else if x == x.Parent.Left { // x是其父节点的左子节点x.Parent.Left = y} else { // x是其父节点的右子节点x.Parent.Right = y}// 将x设置为y的左子节点y.Left = xx.Parent = y// 更新旋转后节点的最大值属性x.maxValue = max(x.Interval.Max(), getMaxOfSubtree(x.Left), getMaxOfSubtree(x.Right))y.maxValue = max(y.Interval.Max(), x.maxValue, getMaxOfSubtree(y.Right))return y // 返回新的子树根节点
}// 辅助函数，获取子树的最大值
func getMaxOfSubtree(node *Node) ValueType {if node == nil {return minValue // 或者根据实际情况返回某个最小值}return node.maxValue
}

这里假设max()函数用于比较并返回两个或多个数值中的最大值，而getMaxOfSubtree()是一个递归辅助函数，用于获取给定节点下整个子树的最大值。由于每个节点都已经预先计算并存储了maxValue，所以在旋转后只需重新计算涉及旋转部分的节点的最大值即可在O(1)时间内完成更新。

在这里插入图片描述

在这里插入图片描述

天工：

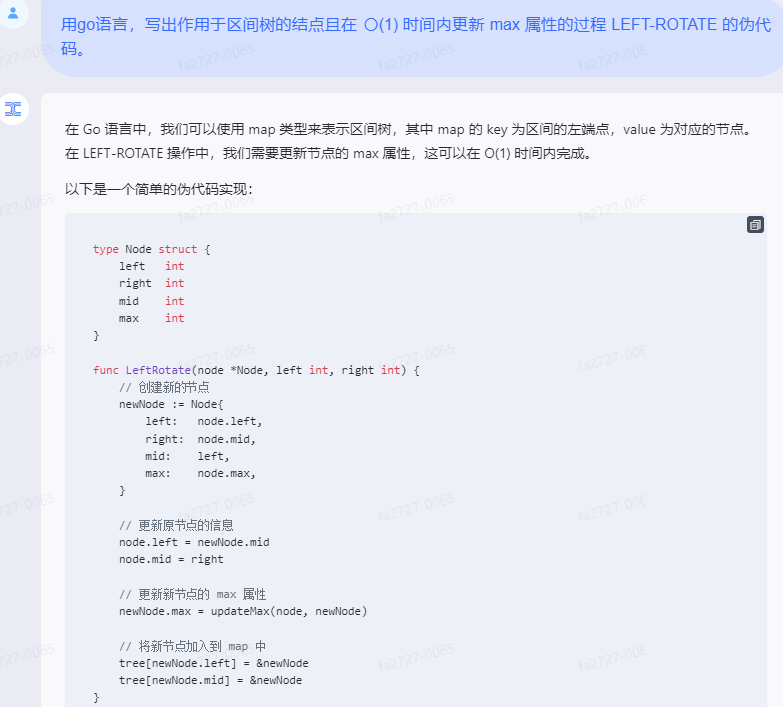
在 Go 语言中，我们可以使用 map 类型来表示区间树，其中 map 的 key 为区间的左端点，value 为对应的节点。在 LEFT-ROTATE 操作中，我们需要更新节点的 max 属性，这可以在 O(1) 时间内完成。

以下是一个简单的伪代码实现：

type Node struct {left   intright  intmid    intmax    int
}func LeftRotate(node *Node, left int, right int) {// 创建新的节点newNode := Node{left:   node.left,right:  node.mid,mid:    left,max:    node.max,}// 更新原节点的信息node.left = newNode.midnode.mid = right// 更新新节点的 max 属性newNode.max = updateMax(node, newNode)// 将新节点加入到 map 中tree[newNode.left] = &newNodetree[newNode.mid] = &newNode
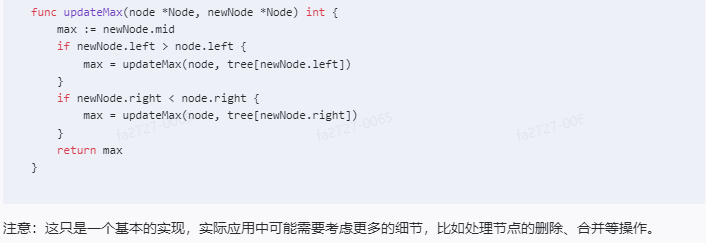
}func updateMax(node *Node, newNode *Node) int {max := newNode.midif newNode.left > node.left {max = updateMax(node, tree[newNode.left])}if newNode.right < node.right {max = updateMax(node, tree[newNode.right])}return max
}

注意：这只是一个基本的实现，实际应用中可能需要考虑更多的细节，比如处理节点的删除、合并等操作。

在这里插入图片描述

在这里插入图片描述

灵小智：

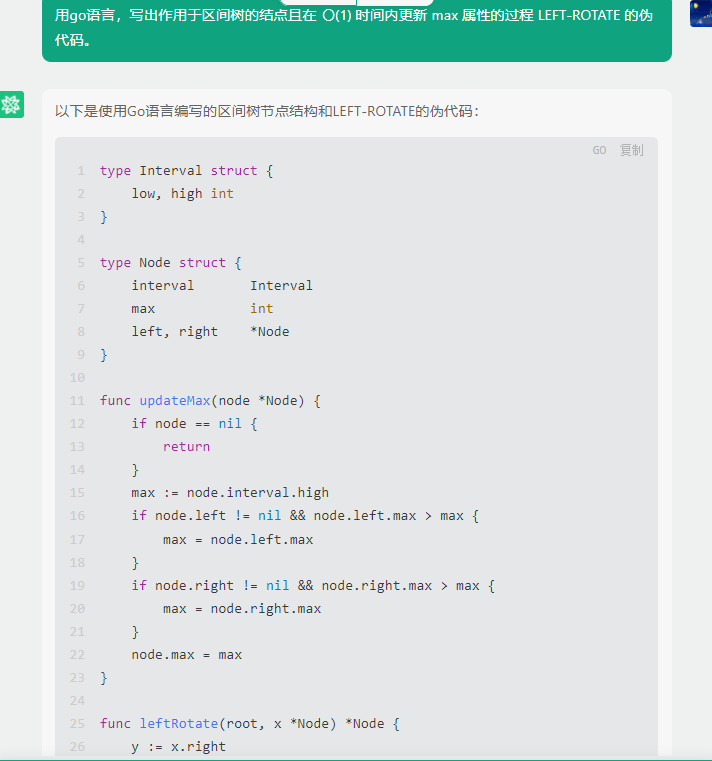
以下是使用Go语言编写的区间树节点结构和LEFT-ROTATE的伪代码：

type Interval struct {low, high int
}type Node struct {interval       Intervalmax            intleft, right    *Node
}func updateMax(node *Node) {if node == nil {return}max := node.interval.highif node.left != nil && node.left.max > max {max = node.left.max}if node.right != nil && node.right.max > max {max = node.right.max}node.max = max
}func leftRotate(root, x *Node) *Node {y := x.rightx.right = y.lefty.left = xupdateMax(x)updateMax(y)if root == x {root = y}return y
}

请注意，这只是LEFT-ROTATE操作的伪代码示例，实际使用中还需要考虑其他边界情况和可能的错误处理。

在这里插入图片描述

在这里插入图片描述

chatgpt：

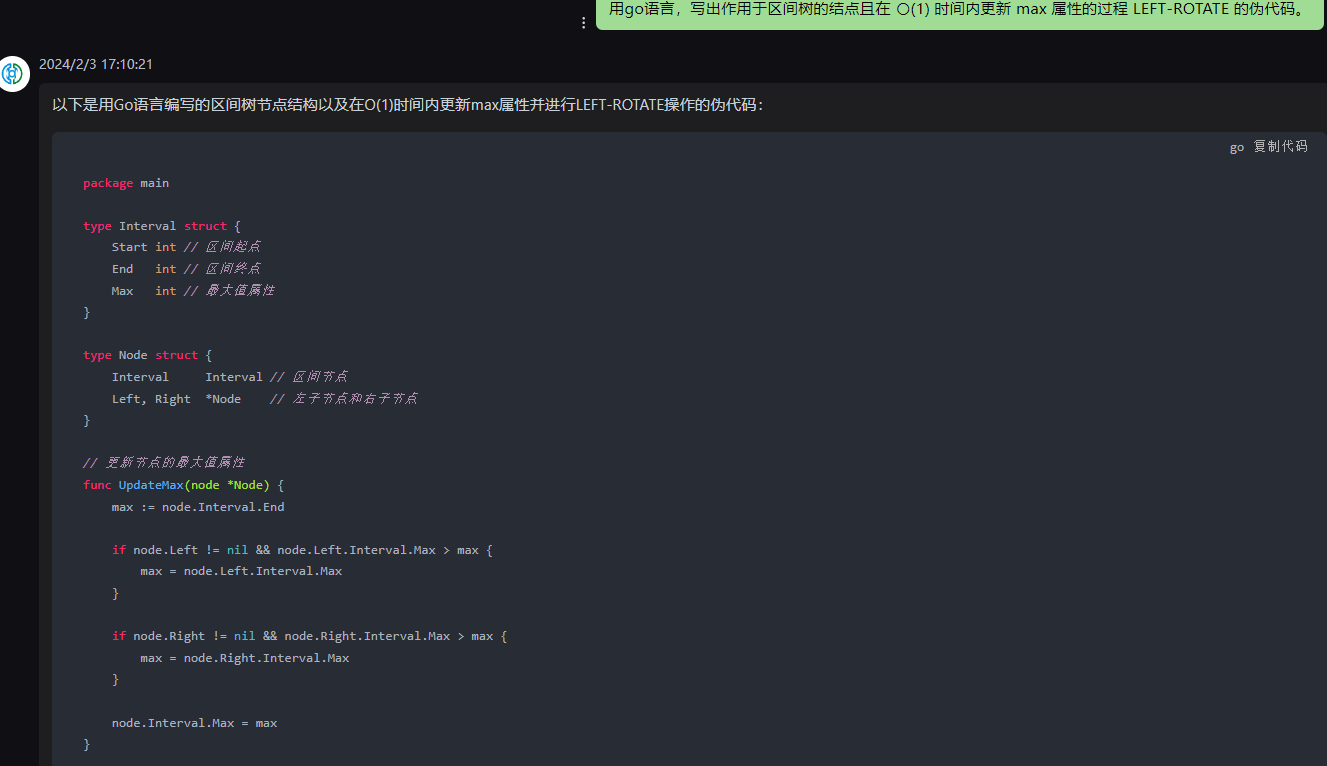
以下是用Go语言编写的区间树节点结构以及在O(1)时间内更新max属性并进行LEFT-ROTATE操作的伪代码：

package maintype Interval struct {Start int // 区间起点End   int // 区间终点Max   int // 最大值属性
}type Node struct {Interval     Interval // 区间节点Left, Right  *Node    // 左子节点和右子节点
}// 更新节点的最大值属性
func UpdateMax(node *Node) {max := node.Interval.Endif node.Left != nil && node.Left.Interval.Max > max {max = node.Left.Interval.Max}if node.Right != nil && node.Right.Interval.Max > max {max = node.Right.Interval.Max}node.Interval.Max = max
}// 左旋转操作（Left-Rotate）
func LeftRotate(root, x *Node) *Node {y := x.Right              // 获取x的右子节点yx.Right = y.Left          // 将y的左子节点作为x的右子节点if y.Left != nil {y.Left.Parent = x       // 设置x为y的左子节点的父节点 }y.Parent = x.Parent         // 设置y的父节点为x的父节点if x.Parent == nil {       // 如果x是根节点，则将y设为新的根节点root = y   } else if x == x.Parent.Left {  // 如果x是其父节点的左子节点，则将y设为其父节点的左子节点  x.Parent.Left = y      } else {                     // 如果x是其父节点的右子节点，则将y设为其父节点的右子节点 x.Parent.Right = y     }y.Left = x                // 将x设为y的左子节点x.Parent = y              // 将y设为x的父节点UpdateMax(x)             // 更新旋转后相关节点的最大值属性UpdateMax(y)return root
}func main() {// 示例代码中只包含了区间树结构和左旋转操作，你可以根据实际需求添加其他操作和方法。
}

这段代码给出了一个基本的区间树结构和LEFT-ROTATE操作，但需要注意的是，具体实现会受到数据结构和算法设计的影响。因此，在实际应用中，请根据自己的需求进行适当修改和优化。

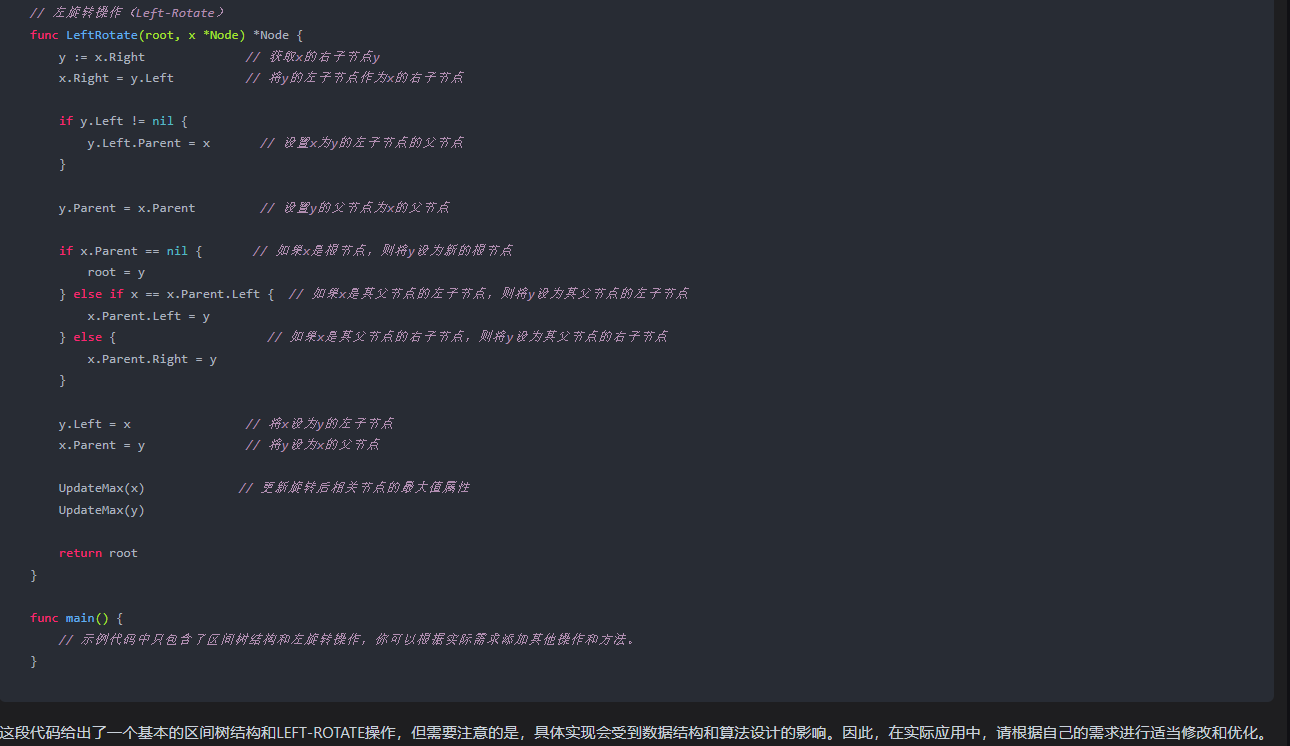
在这里插入图片描述

在这里插入图片描述

kimi：

在区间树（Interval Tree）中，节点通常包含一个区间（通常是左端点和右端点）以及一个关联值。在进行左旋操作（LEFT-ROTATE）时，我们通常需要更新节点的 max 属性，以确保它反映了子树中的最大值。以下是一个作用于区间树节点的左旋操作的伪代码，它在 O(1) 时间内更新 max 属性：

// 假设我们有一个区间树节点结构体
type IntervalNode struct {interval [2]int // [left, right]value    intmax      int // 最大值left     *IntervalNoderight    *IntervalNode
}// LEFT-ROTATE 函数
func leftRotate(x *IntervalNode) *IntervalNode {// 保存 x 的右子节点y := x.right// 将 y 的左子节点设置为 x 的右子节点x.right = y.left// 如果 y 的左子节点不为空，更新其父指针if y.left != nil {y.left.parent = x}// 更新 y 的父指针y.parent = x.parent// 如果 x 是根节点，更新根节点if x.parent == nil {root = y} else {// 如果 x 是其父节点的左子节点if x.parent.left == x {x.parent.left = y} else {// 如果 x 是其父节点的右子节点x.parent.right = y}}// 将 y 的左子节点设置为 xy.left = x// 更新 x 的父指针x.parent = y// 更新 x 和 y 的 max 属性x.max = max(x.value, x.right.max)y.max = max(y.value, y.left.max)// 返回新的根节点return y
}// max 辅助函数
func max(a, b int) int {if a > b {return a}return b
}

在这个伪代码中，我们首先定义了一个 IntervalNode 结构体，它包含了区间树节点的所有必要信息。leftRotate 函数执行左旋操作，同时更新 x 和 y 的 max 属性。在旋转过程中，我们确保了 max 属性始终反映子树中的最大值。

请注意，这个伪代码假设每个节点都有一个指向其父节点的指针 parent，这在实际的区间树实现中是必要的。在实际的 Go 代码中，你可能需要根据具体的区间树实现来调整这个伪代码。

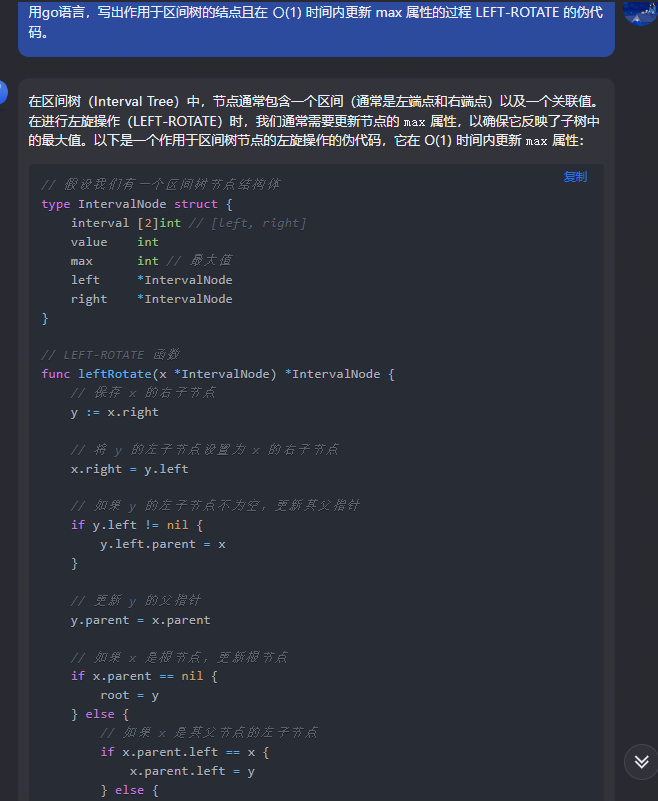
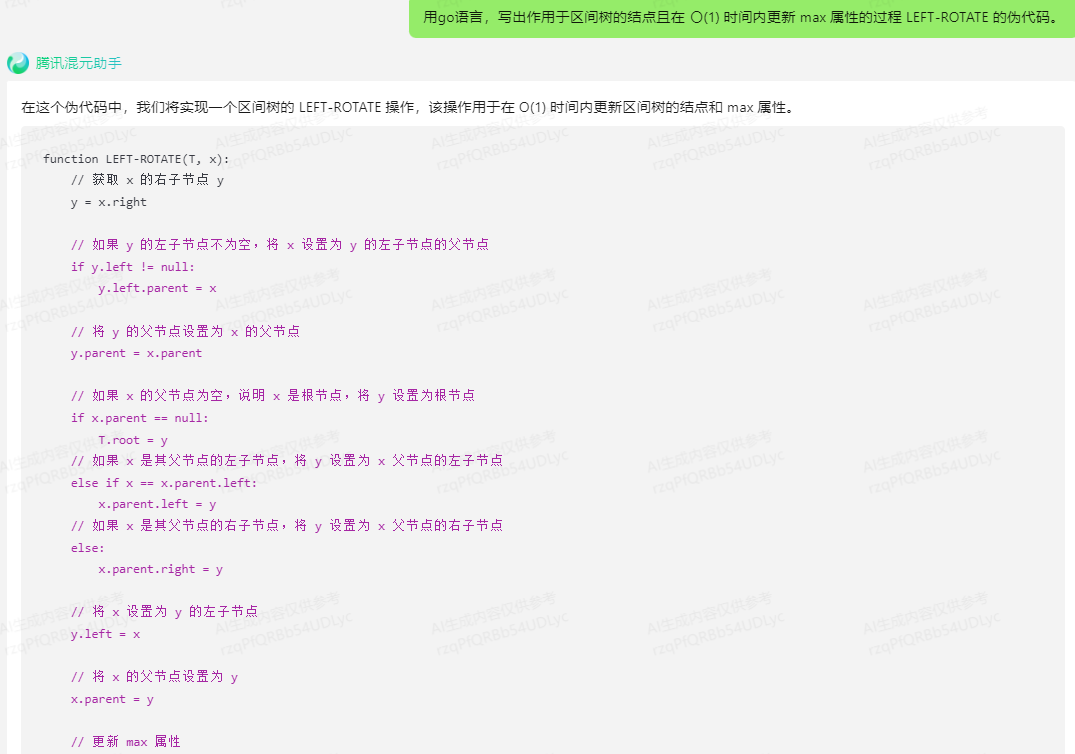
在这里插入图片描述

在这里插入图片描述

混元：

在这个伪代码中，我们将实现一个区间树的 LEFT-ROTATE 操作，该操作用于在 O(1) 时间内更新区间树的结点和 max 属性。

function LEFT-ROTATE(T, x):// 获取 x 的右子节点 yy = x.right// 如果 y 的左子节点不为空，将 x 设置为 y 的左子节点的父节点if y.left != null:y.left.parent = x// 将 y 的父节点设置为 x 的父节点y.parent = x.parent// 如果 x 的父节点为空，说明 x 是根节点，将 y 设置为根节点if x.parent == null:T.root = y// 如果 x 是其父节点的左子节点，将 y 设置为 x 父节点的左子节点else if x == x.parent.left:x.parent.left = y// 如果 x 是其父节点的右子节点，将 y 设置为 x 父节点的右子节点else:x.parent.right = y// 将 x 设置为 y 的左子节点y.left = x// 将 x 的父节点设置为 yx.parent = y// 更新 max 属性x.max = max(x.left.max, x.right.max)y.max = max(y.left.max, y.right.max)

这个伪代码实现了 LEFT-ROTATE 操作，它在 O(1) 时间内更新了区间树的结点和 max 属性。注意，这个伪代码假设了区间树的结点具有 left、right、parent 和 max 属性。

在这里插入图片描述

在这里插入图片描述

这篇关于文心一言 VS 讯飞星火 VS chatgpt （193）-- 算法导论14.3 1题的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/676588。

相关文章

SpringBoot实现MD5加盐算法的示例代码

SpringBoot实现MD5加盐算法的示例代码

《SpringBoot实现MD5加盐算法的示例代码》加盐算法是一种用于增强密码安全性的技术,本文主要介绍了SpringBoot实现MD5加盐算法的示例代码,文中通过示例代码介绍的非常详细,对大家的学习... 目录一、什么是加盐算法二、如何实现加盐算法2.1 加盐算法代码实现2.2 注册页面中进行密码加盐2.
阅读更多...
基于Flask框架添加多个AI模型的API并进行交互

基于Flask框架添加多个AI模型的API并进行交互

《基于Flask框架添加多个AI模型的API并进行交互》：本文主要介绍如何基于Flask框架开发AI模型API管理系统,允许用户添加、删除不同AI模型的API密钥,感兴趣的可以了解下... 目录1. 概述2. 后端代码说明2.1 依赖库导入2.2 应用初始化2.3 API 存储字典2.4 路由函数2.5 应
阅读更多...
Java时间轮调度算法的代码实现

Java时间轮调度算法的代码实现

《Java时间轮调度算法的代码实现》时间轮是一种高效的定时调度算法,主要用于管理延时任务或周期性任务,它通过一个环形数组（时间轮）和指针来实现,将大量定时任务分摊到固定的时间槽中,极大地降低了时间复杂... 目录1、简述2、时间轮的原理3. 时间轮的实现步骤3.1 定义时间槽3.2 定义时间轮3.3 使用时
阅读更多...
Spring AI ectorStore的使用流程

Spring AI ectorStore的使用流程

《SpringAIectorStore的使用流程》SpringAI中的VectorStore是一种用于存储和检索高维向量数据的数据库或存储解决方案,它在AI应用中发挥着至关重要的作用,本文给大家介... 目录一、VectorStore的基本概念二、VectorStore的核心接口三、VectorStore的
阅读更多...
如何通过Golang的container/list实现LRU缓存算法

如何通过Golang的container/list实现LRU缓存算法

《如何通过Golang的container/list实现LRU缓存算法》文章介绍了Go语言中container/list包实现的双向链表,并探讨了如何使用链表实现LRU缓存,LRU缓存通过维护一个双向... 目录力扣：146. LRU 缓存主要结构 List 和 Element常用方法1. 初始化链表2.
阅读更多...
Spring AI集成DeepSeek三步搞定Java智能应用的详细过程

Spring AI集成DeepSeek三步搞定Java智能应用的详细过程

《SpringAI集成DeepSeek三步搞定Java智能应用的详细过程》本文介绍了如何使用SpringAI集成DeepSeek,一个国内顶尖的多模态大模型,SpringAI提供了一套统一的接口,简... 目录DeepSeek 介绍Spring AI 是什么？Spring AI 的主要功能包括1、环境准备2
阅读更多...
Spring AI集成DeepSeek实现流式输出的操作方法

Spring AI集成DeepSeek实现流式输出的操作方法

《SpringAI集成DeepSeek实现流式输出的操作方法》本文介绍了如何在SpringBoot中使用Sse（Server-SentEvents）技术实现流式输出,后端使用SpringMVC中的S... 目录一、后端代码二、前端代码三、运行项目小天有话说题外话参考资料前面一篇文章我们实现了《Spring
阅读更多...
Spring AI与DeepSeek实战一之快速打造智能对话应用

Spring AI与DeepSeek实战一之快速打造智能对话应用

《SpringAI与DeepSeek实战一之快速打造智能对话应用》本文详细介绍了如何通过SpringAI框架集成DeepSeek大模型,实现普通对话和流式对话功能,步骤包括申请API-KEY、项目搭... 目录一、概述二、申请DeepSeek的API-KEY三、项目搭建3.1. 开发环境要求3.2. mav
阅读更多...
C#集成DeepSeek模型实现AI私有化的流程步骤(本地部署与API调用教程)

C#集成DeepSeek模型实现AI私有化的流程步骤(本地部署与API调用教程)

《C#集成DeepSeek模型实现AI私有化的流程步骤(本地部署与API调用教程)》本文主要介绍了C#集成DeepSeek模型实现AI私有化的方法,包括搭建基础环境,如安装Ollama和下载DeepS... 目录前言搭建基础环境1、安装 Ollama2、下载 DeepSeek R1 模型客户端 ChatBo
阅读更多...
golang字符串匹配算法解读

golang字符串匹配算法解读

《golang字符串匹配算法解读》文章介绍了字符串匹配算法的原理,特别是Knuth-Morris-Pratt（KMP）算法,该算法通过构建模式串的前缀表来减少匹配时的不必要的字符比较,从而提高效率,在... 目录简介KMP实现代码总结简介字符串匹配算法主要用于在一个较长的文本串中查找一个较短的字符串（称为
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2