文心一言专题

文心一言功能新升级：读文档、懂翻译、能识图

9月4日，百度文心一言官网显示，在向全社会开放一周年之际，文心一言进行了功能最新全面升级，同时在周年期间为新老会员增加1个月专业版免费使用体验。据了解，针对网页版用户需求，文心一言实现了创作内容更加深度专业、问答效果更加全面丰富、支持同时处理上百个多种格式文件、一键关联读取网盘文档、智能翻译和图片理解等能力的升级，全面满足用户多场景专业需求。在专业创作领域，文档分析是一种被频

百度文心一言 App 获推 4.0.0 版本升级：更名文小言、9 月内文心 4.0 大模型免费用！

百度文心一言 App 获推 4.0.0 版本升级：更名文小言、9 月内文心 4.0 大模型免费用！文小言4.0.0版本重磅发布：AI新时代的引领者！💥 随着科技的飞速发展，AI已经深入到我们生活的方方面面。2024年9月，百度正式发布了文心一言App的4.0.0版本，并更名为**“文小言”**。这一升级不仅象征着技术的飞跃，也预示着AI能力即将更广泛应用到日常场景中。那么，这款备受关注的A

文心一言 VS 讯飞星火 VS chatgpt （339）-- 算法导论23.1 8题

八、设 T T T为图 G G G的一棵最小生成树，设 L L L为树 T T T中一个边权重的有序列表。证明：对于图 G G G的任何其他最小生成树 T ′ T' T′，列表 L L L也是 T ′ T' T′中一个边权重的有序列表。如果要写代码，请用go语言。文心一言：要证明对于图 G G G的任何其他最小生成树 T ′ T' T′，列表 L L L（作为树 T T T的边权重有序列表

文心一言 VS 讯飞星火 VS chatgpt （331）-- 算法导论22.5 7题

七、给定有向图 G = ( V ， E ) G=(V，E) G=(V，E)，如果对于所有结点对 u , v ∈ V u,v∈V u,v∈V,我们有 u → v u→v u→v或 v → u v→u v→u，则 G G G是半连通的。请给出一个有效的算法来判断图 G G G是否是半连通的。证明算法的正确性并分析其运行时间。如果要写代码，请用go语言。文心一言：为了判断一个有向图是否是半连通

【AI】准备放弃“文心一言”，不再续费

百度真是把一手好牌打的稀烂，最近感觉文心一言起步很猛，但是能力越来越差。不要说毫无技术极客精神，几乎没有斗志和追求了。有2个案例，让我非常的失望。第一个案例体现了它的不诚实，过度的商业“考量”。第二个案例体现了它的不专业。第一个提示词对比：开源大模型我的提示词是：国产开源大模型有哪些，给我3-5个例子。文心一言是这样回答我的：国产开源大模型在近年来取得了显著的发展，

解锁黑科技！百度AppBuilder助你秒变开发者，轻松实现文心一言

在数字化浪潮席卷全球的今天，人工智能（AI）和大模型技术正以前所未有的速度改变着我们的世界。从自然语言处理到图像识别，从智能推荐到自动化决策，大模型以其强大的数据处理能力和学习能力，正成为推动科技创新的核心动力。然而，对于许多开发者而言，如何高效、便捷地将大模型的能力集成到自己的应用中，却是一个不小的挑战。此时，一款强大且易于使用的应用开发工具就显得尤为重要。本篇文章就教同学们如何基于Ap

文心一言 VS 讯飞星火 VS chatgpt （287）-- 算法导论21.2 6题

六、假设对 UNION 过程做一个简单的改动，在采用链表表示中拿掉让集合对象的 tail 指针总指向每个表的最后一个对象的要求。无论是使用还是不使用加权合并启发式策略，这个修改不应该改变 UNION 过程的渐近运行时间。(提示:而不是把一个表链接到另一个表后面，将它们拼接在一起。)如果要写代码，请用go语言。文心一言：在并查集（Union-Find）数据结构中，UNION 过程通常用于合并

git分支及提交规范【AI 文心一言】

Git代码提交规范和分支命名规范是团队协作中非常重要的部分，它们有助于保持代码库的清晰、一致和易于管理。以下是对Git代码提交规范和采用“/”分割的分支命名规范的总结： Git代码提交规范提交类型： feat: 增加新功能 fix: 修复问题BUG docs: 文档更新 style: 代码格式（不影响代码运行的变动）例如去掉空格、改变缩进、增删分 refactor: 代码重构（既不是修复bu

五大维度大比拼：ChatGPT比较文心一言，你的AI助手选择指南

文章目录一、评估AI助手的五个关键维度二、ChatGPT和文心一言的比较评估AI助手的五个关键维度，以及ChatGPT和文心一言的比较如下：一、评估AI助手的五个关键维度界面友好性：评估标准：用户界面是否直观易用，是否便于用户与AI助手交流。重要性：友好的界面能够降低用户的学习成本，提高使用效率。交互效率：评估标准：用户达到目的所需的步骤是否简洁。重要性

【AI原理解析】— 文心一言模型

目录模型架构 Transformer模型编码器-解码器结构训练过程预训练微调关键技术知识增强上下文感知个性化生成推理与生成应用场景问答系统文本生成对话系统模型架构 Transformer模型文心一言的核心架构采用了Transformer模型，该模型是一种基于自注意力机制的神经网络结构。它能够处理变长序列，并通过自注意力机制

【AI应用探讨】— 文心一言模型应用场景

目录学习助手学科知识点查询学习资料搜索工作辅助信息查询内容创作生活助手日常问题解答生活建议智能客服客户问题解答提升客户体验智能家居语音控制智能场景设置金融领域投资咨询风险评估医疗健康领域医疗咨询健康监测内容优化与编辑文本纠错内容优化学习助手学科知识点查询学生可以通过我快速查询数学、物

文心一言 VS 讯飞星火 VS chatgpt （280）-- 算法导论20.4 1题

一、假设 CONNECTED-COMPONENTS 作用于一个无向图 G=(V，E)，这里V={a，b，c，d，e，f，g，h，i，j，k}，且 E 中的边以如下的顺序处理:(d,i),(f,k),(g,i),(b,g),(a,h),(i,j),(d,k),(b,j),(d,f),(g,j),(a,e)。请列出在每次执行完第3~5行后各连通分量的顶点。如果要写代码，请用go语言。文心一言：

【AI】文心一言的使用分享

在数字化时代，人工智能（AI）技术的飞速发展正在改变我们的生活。文心一言，作为这一浪潮中的佼佼者，以其卓越的自然语言处理能力和广泛的应用场景，给我带来了前所未有的使用体验。在这篇分享中，我将详细阐述我对文心一言的使用体验、功能特点、应用场景以及未来展望。一、初识文心一言首次接触文心一言，我便被其强大的自然语言处理能力所吸引。这款AI模型能够准确理解人类的语言，无论是简单的日常对话还是复

文心一言 VS 讯飞星火 VS chatgpt （279）-- 算法导论20.3 6题

六、创建一个全域大小为 u 的 vEB 树，需要 O(u) 的运行时间。假设我们想得到确切时间。如果 vEB 树中每个操作的摊还时间为〇(lglgu)，那么最小的操作数 n 是多少？如果要写代码，请用go语言。文心一言：首先，让我们澄清一下 vEB（van Emde Boas）树的基本概念。vEB 树是一种特殊的搜索树，用于存储在一个小的连续整数集合中的元素。其特性在于，当集合中的元素数

文心一言 VS 讯飞星火 VS chatgpt （278）-- 算法导论20.3 5题

五、假设我们创建一个包含 u 1 k u^\frac{1}{k} uk1 个簇(而不是全域大小为 x ↓ {\sqrt[↓]{x}} ↓x 的 x ↑ {\sqrt[↑]{x}} ↑x 个簇)的 vEB 树，其每个簇的全域大小为 u 1 − 1 k u ^ {1-\frac{1}{k}} u1−k1 ，其中 k>1 ，而且 k 为常数。如果恰当地修改这些操作，则这些操作

android集成百度文心一言实现对话功能，实战项目讲解，人人都能拥有一款ai应用

大家好，今天给大家讲解下如何实现一个基于百度文心一言的app功能，app内部同时集成了讯飞的语音识别。本文适用于有android基础的小伙伴阅读，文章末尾放上本项目用到的全部实例代码，在使用前请务必看完本文章。先来给大家看看效果。百度文心一言API权限申请及创建应用第一步：打开百度文心一言的api开发者平台-千帆百度智能云千帆大模型平台ModelBuilder 第二步

文心一言 VS 讯飞星火 VS chatgpt （272）-- 算法导论20.2 7题

七、试说明如果 PROTO-vEB-MINIMUM 中的第 9 行被执行，则proto-vEB 结构为空。如果要写代码，请用go语言。文心一言：在 PROTO-vEB-MINIMUM 算法中，我们假设你指的是一个基于位向量（bit-vector）的扩展二进制树（vEB tree）的原型实现，其中 MINIMUM 操作用于找到树中的最小元素。如果第 9 行被执行，这通常意味着在搜索最小元素时

国内AI工具访问量第一的竟然是它？！不是Kimi，也不是文心一言

大家好，我是木易，一个持续关注AI领域的互联网技术产品经理，国内Top2本科，美国Top10 CS研究生，MBA。我坚信AI是普通人变强的“外挂”，所以创建了“AI信息Gap”这个公众号，专注于分享AI全维度知识，包括但不限于AI科普，AI工具测评，AI效率提升，AI行业洞察。关注我，AI之路不迷路，2024我们一起变强。如果要说国内AI工具一哥是谁？很多小伙伴肯定第一时间想到Kimi或

文心一言 VS 讯飞星火 VS chatgpt （269）-- 算法导论20.2 4题

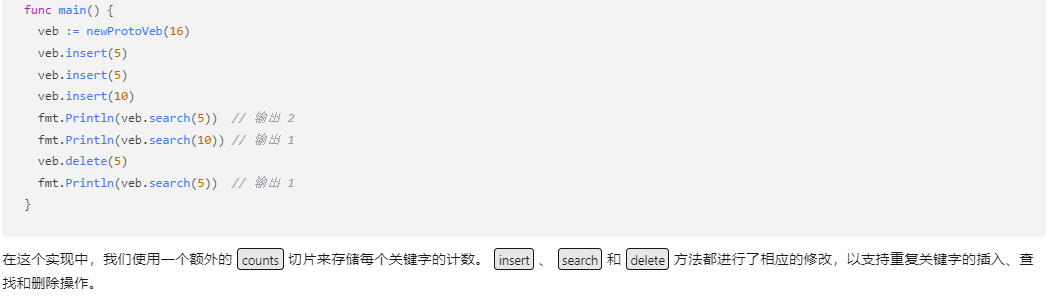
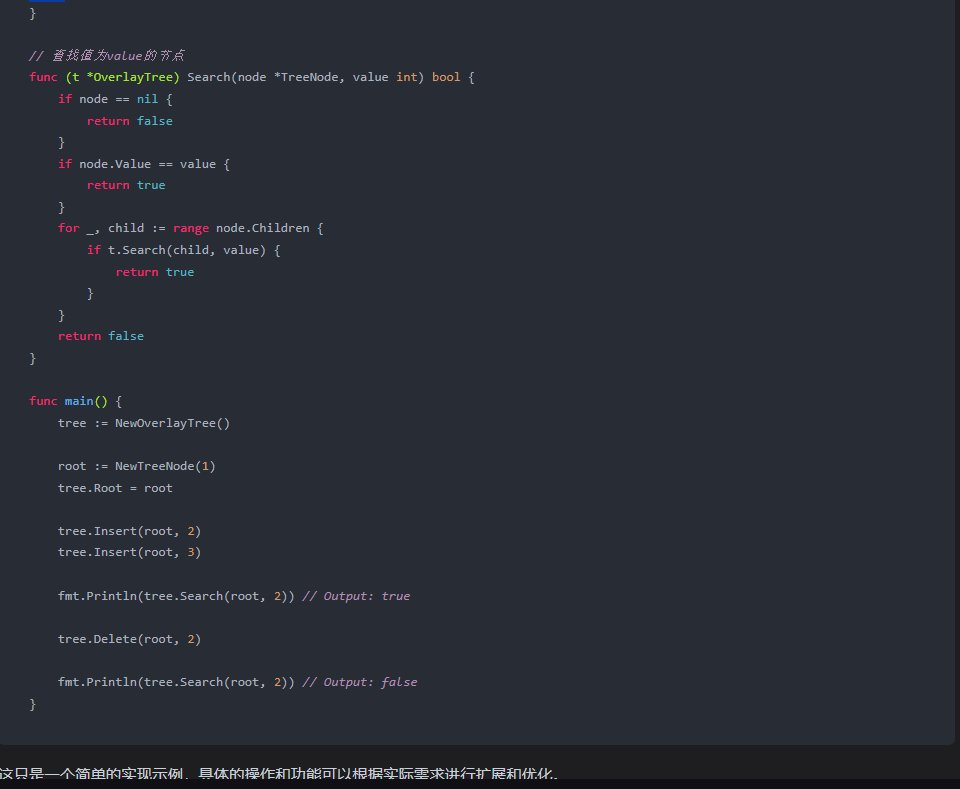
四、修改 proto-vEB 结构，以支持重复关键字。如果要写代码，请用go语言。文心一言：在原始的 van Emde Boas 树（vEB tree）结构中，关键字（key）是唯一的，不允许有重复的关键字。然而，如果你想要修改这个结构以支持重复的关键字，你可以将每个关键字映射到一个集合（如列表或切片），而不是单个值。在Go语言中，你可以使用map来实现这样的结构，其中map的键是关键

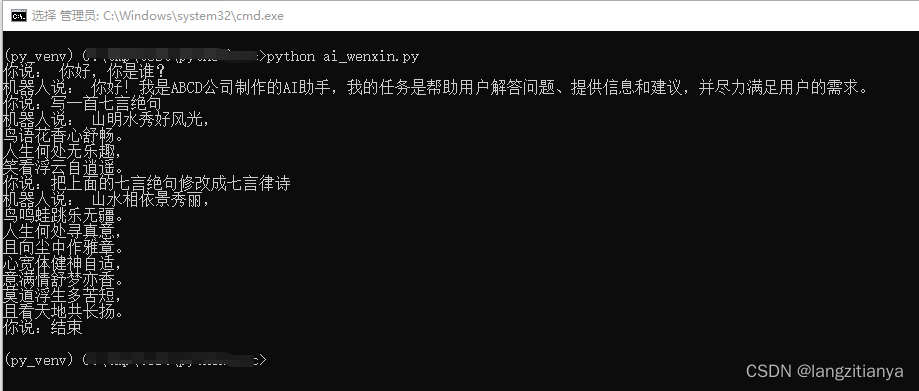
python调用百度文心一言对话模型

近日，百度宣布其两款主力模型 ENIRE Speed、ENIRE Lite 可以免费使用。试了一下怎么程序调用。 1.准备工作需要注册百度智能云账号，也可以使用原来的百度账号登录，登录之后要完成实名认证，才能使用API调用。在千帆大模型操作台 ->模型服务->在线服务->预置服务里开通需要调用的模型。本次测试开通了ERNIE-Speed-128K的调用。在安全认证页面，取得Access

文心一言 VS 讯飞星火 VS chatgpt （265）-- 算法导论20.1 4题

四、假设不使用一棵叠加的度为 u \sqrt{u} u 的树，而是使用一棵叠加的度为 u 1 k u^{\frac{1}{k}} uk1的树，这里 k 是大于 1 的常数，则这样的一棵树的高度是多少？又每个操作将需要多长时间？如果要写代码，请用go语言。文心一言：在这个场景中，我们讨论的是一种特殊的树结构，其中节点的度（即子节点的数量）是 u^(1/k)，u 是树中元素的总数，

文心一言智能体-心弦共鸣

文章目录引言文心一言智能体小程创建的智能体——心弦共鸣核心设计理念功能设计应用场景未来展望引言在数字世界的深邃海洋中，有一片由智慧与创新编织的新天地——文心一言智能体平台。在这里，每一个智能体都如同星辰般璀璨，它们不仅承载着技术的光辉，更蕴含着创造者的无限想象。文心一言智能体链接:link 小程创建的智能体——心弦共鸣链接: link “心弦共鸣”诞生

文心一言指令多样化，你知道的有哪些？

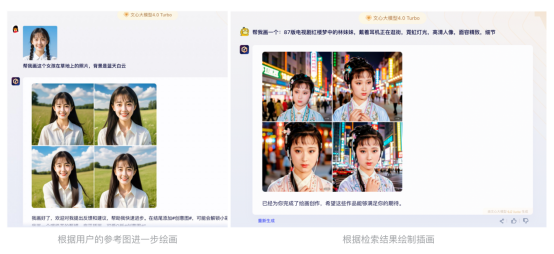
文心一言的指令非常多样化，可以根据用户的需求和场景进行灵活调整。以下是一些常见的文心一言指令示例：知识问答：帮我解释一下什么是芯片？中国的历史上有哪些重要的朝代？人工智能在未来会有哪些发展趋势？文本创作：帮我写一首关于秋天的诗。生成一篇关于环保的演讲稿。创作一个关于未来城市的科幻故事。图像生成：帮我画一个在草丛里打架的小猫咪。生成一幅唐朝美女的画像，面容精致妖媚，红衣。创作一幅关于太

文心一言 VS 讯飞星火 VS chatgpt （259）-- 算法导论19.3 2题

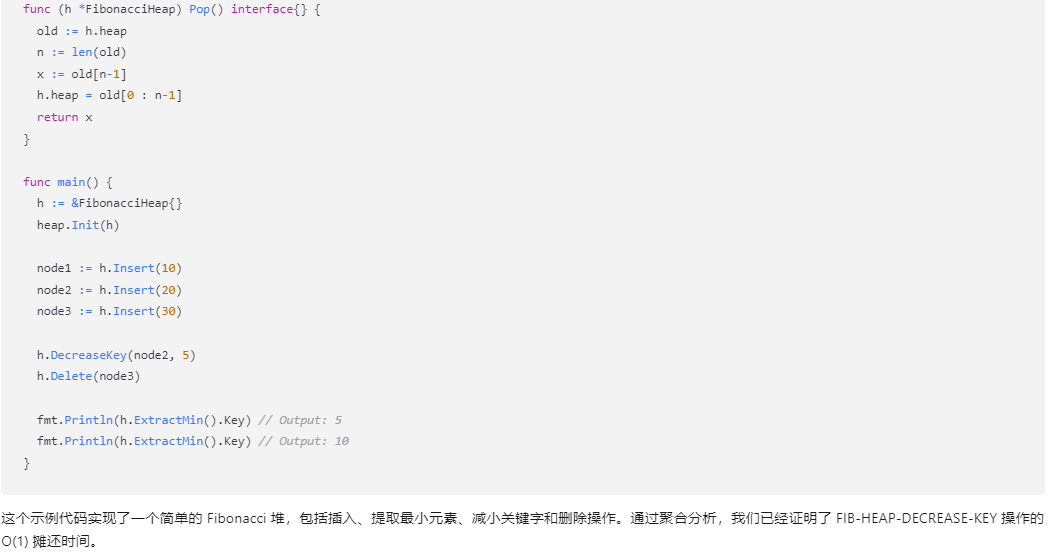
二、使用聚合分析来证明 FIB-HEAP-DECREASE-KEY 的 O(1) 摊还时间是每一个操作的平均代价。如果要写代码，请用go语言。文心一言： FIB-HEAP-DECREASE-KEY 是斐波那契堆（Fibonacci Heap）操作中的一个，它允许我们减少堆中某个节点的键值，并可能触发一系列操作来维护堆的性质。然而，直接证明 FIB-HEAP-DECREASE-KEY 的摊还时

百度文心一言 java 支持流式输出，Springboot+ sse的demo

参考：GitHub - mmciel/wenxin-api-java: 百度文心一言Java库，支持问答和对话，支持流式输出和同步输出。提供SpringBoot调用样例。提供拓展能力。 1、依赖 <dependency> <groupId>com.baidu.aip</groupId> <artifactId>java-sdk</artifactId> <version>4.16

文心一言指令：引领语言模型的创新之路

文心一言指令：引领语言模型的创新之路引言在人工智能领域，尤其是自然语言处理（NLP）的世界中，语言模型的发展一直是科技进步和创新的前沿。随着深度学习技术的突破，一系列强大的语言模型如雨后春笋般涌现，它们在不同的应用场景中展现出惊人的能力。在这样的背景下，"文心一言"指令的概念应运而生，它不仅是一个技术概念，更是一种对语言模型未来发展的深刻洞察和期待。什么是文心一言指令 "文心一言"指