卡尔曼滤波算法-DTN中一种基于灰色预测和状态估计的位置预测方法

本文主要是介绍卡尔曼滤波算法-DTN中一种基于灰色预测和状态估计的位置预测方法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

卡尔曼滤波算法

一、基本思想

在实际应用中，常常需要知道实际的物理量的值，但事实上我们很难获得实际系统状态的实际值，因此我们需要对实际物理量的值进行估计。

卡尔曼滤波器主要用于对实际系统状态的估计上，其算法思想是：
估计值=预测+更新
解释：根据系统状态在0,1,…,k-1时刻的估计值，预测k时刻的值x^(k|k-1)。再通过k时刻传感器的值来对预测值进行更新，更新的方法是基于最小均方误差原理，最终得到估计值x ^(k)。

下面有两个例子便于理解。

案例一

有一条回家的路，你每天都开汽车走，因此对这条路非常熟悉了。有一天，有个人要求你把车窗用木板都封住，开车走这条路回家，你会如何做？

应用卡尔曼滤波的思想：预测+测量更新

1.由于这条路你已经非常熟悉了，所以会根据走了多长时间，路面是否崎岖等条件判断你走到哪了。
2.开启车载GPS，GPS会告诉你你的确切位置，心里有了底。
3.将自身经验（预测）和GPS（测量）融合在一起，判断自己走到哪里了。
舒服。

案例二

已知k-1时刻室内温度是23度，你在室内且室内装有温度计，问你k时刻温度估计是多少？

应用卡尔曼滤波的思想：预测+测量更新

1.因为你在室内，所以你基于自身感觉做出判断，你感觉温度没啥变化呀，所以你预测k时刻也是23度
2.严谨来说，你不敢准确就是23度，你说上下浮动2度（方差）吧，即23±2，这是你的预测值
3.你看了一眼温度计，嗯温度计显示k时刻是25度。
4.然后你又查了查温度计说明书，它说温度计有0.5度（方差）的浮动，即25±0.5，这是温度计的测量值
所以你把预测值和测量值进行融合，怎么融合呢？你的想法是二者加权和，且浮动值越大越不准确，因此估计结果中浮动值大的应该占比更小。所以你根据浮动值计算出估计结果。
即
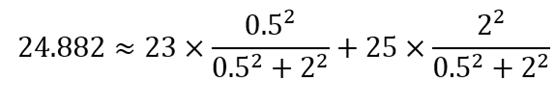
在这里插入图片描述

二、预备知识

1.方差：所有样本值与样本均差值的平方和的平均数，表征变量的离散程度，表达的是变量与期望值之间的距离。
2.协方差：表达变量间的相关程度，当变量全部相同时就变成了方差。
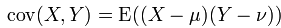
cov(X,Y)=E((X-μ)(Y-v))

3.高斯分布：即正态分布，其概率密度函数如下图所示，其均值为μ，方差为σ2，记作X~N(μ,σ2)
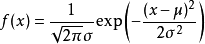
在这里插入图片描述

4.先验和后验：先验是指直接判断，后验是做了手脚之后判断，或叫条件值。例如，三个扣着放的不透明碗ABC，有且仅有一只碗下面有个球，问A碗有球的概率，答1/3，这是先验概率。打开B碗发现B碗没球，问A碗有球的概率，答1/2，这是后验概率。
5.最小均方误差MSE：被估计的量和估计量之间的误差的均值最小，即min E(e2)

三、算法原理

卡尔曼滤波算法是考虑了系统在实际情况下会受到外界扰动这一具体事实，因此比单纯理论计算有更高的实践性。
卡尔曼假设实际系统会受到均值为0的高斯分布的白噪声影响，同时传感器也会受到均值为0的高斯白噪声影响。

算法首先对k时刻的状态进行预测，再利用传感器观测值进行更新，更新方法涉及到噪声和MSE理论。

假设

1.系统和传感器均存在零均值高斯分布的误差。
2.系统模型准确，且系统初始估计值能准确描述系统初始分布，则所有的误差、残差均值为0。

预测

首先，定义k时刻系统的实际状态为：
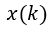
在这里插入图片描述
以及实际系统的状态空间表达式，我们认为存在与系统状态相互独立的高斯噪声wk：

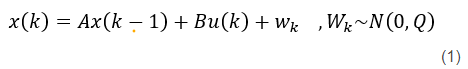
式（1）中wk为随机的噪声值，且只有A,B,u(k)和Q我们已知。
定义k-1时刻的估计值

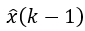
定义k时刻的先验预测值（先验指看传感器读数之前的预测值）
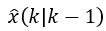
在这里插入图片描述
预测步骤要做的就是根据k-1的估计值来得到k时刻的预测值（也叫先验估计值），根据实际系统状态空间式（1）

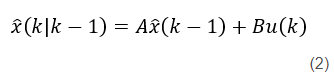
更新

在定义k时刻传感器显示值（常数）为
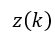
在这里插入图片描述
以及传感器的状态空间表达式，z(k)的值和矩阵H已知，认为存在与系统独立的高斯噪声Vk

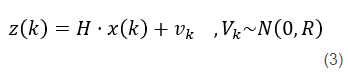
现在有了k时刻的预测值和k时刻的传感器读数，那如何进行更新呢？
将两个值加权就得到了后验值，即后验估计值
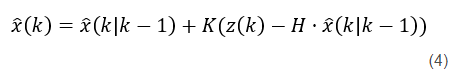
在这里插入图片描述
式子中的K就是卡尔曼增益，K的计算便用到最小均方误差的方法。

最小均方误差

最小均方误差的思想就是实际量x(k)和后验估计量x^(k)的差的平方均值最小，则问题变成
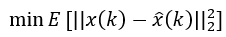
在这里插入图片描述
其实就是

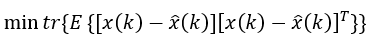
其中tr(.)表示矩阵的迹，即对角线元素的平方和。
根据假设，显然后验估计值的误差协方差就为

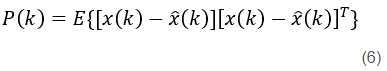
同时先验估计误差的协方差为

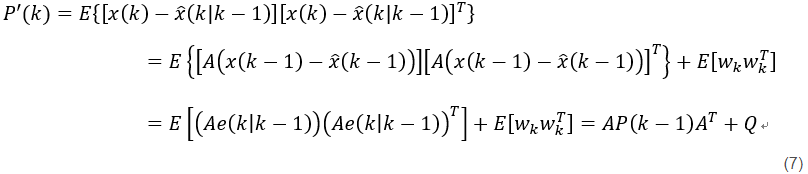
则联合先验估计值表达式（2）、后验估计值表达式（4）和先验估计值协方差式（7），求解后验估计值协方差式（8）为
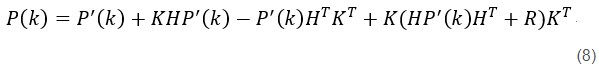
在这里插入图片描述
再根据最小均方误差式子（5），直接对P(k)的迹求导数得0，算得卡尔曼增益K为

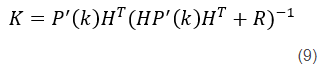
再将先验估计值表达式子（2）和卡尔曼增益K表达式（9）代入后验估计值表达式（4）得到k时刻后验估计值为

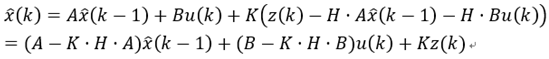
同时还要计算出k时刻后验估计量的方差，以开始下次迭代，即将卡尔曼增益K表达式（9）代入后验估计值协方差式（8）

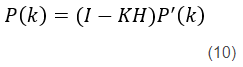
在这里插入图片描述

算法步骤

卡尔曼滤波算法伪代码

KalmanFilter(matrix[] A,matrix[] B,matrix[] Q,matrix[] u,matrix[] z,matrix[] H,matrix[] R,int initialstate,int time)
//输入变量说明
//矩阵A、矩阵B为实际系统状态空间表达式系数矩阵，Q为实际系统高斯噪声方差，u为系统输入列向量，见式(1)
//列向量z为测量值,H为传感器的系数矩阵，R为传感器高斯噪声方差，见式(3)
//initialstate为系统状态初始估计值
//整数time为终止时刻matrix[] xhat;	//系统状态估计值
xhat(0)=initialstate;for k=1:timexhat(k|k-1)=A*xhat(k-1)+B*u(k);	//先验估计值，式(2)P'(k)=A*P(k-1)*A'+Q;	//先验估计误差协方差，式(7)K=P'(k)*H'*inv(H*P'(k)*H'+R);	//卡尔曼增益矩阵K，式(9)xhat(k)=xhat(k|k-1)+K*(z(k)-H*xhat(k|k-1));	//后验估计值，式(4)P(k)=(I-K*H)*P'(k);		//后验估计误差协方差，式(10)
endreturn xhat(time);

卡尔曼滤波器的原理就是预测+更新+最小均方误差

算法拓展

残差

残差定义为估计值与传感器值的差
在卡尔曼滤波算法中，估计值包括先验估计值和后验估计值，卡尔曼假设认为这两个估计值和传感器值的差均值恒为0。
根据残差定义以及先验估计误差协方差式（7）得到先验估计残差：

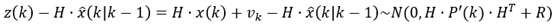
根据残差定义以及后验估计误差协方差式（6）得到后验估计残差
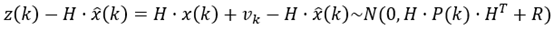
在这里插入图片描述

估计误差

估计误差为实际值与后验估计值的差，即
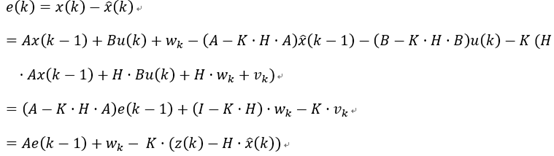
在这里插入图片描述
估计误差与残差的关系

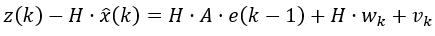
可通过实际数据计算，并与残差分布做比较，进而对数据可靠性、其他干扰进行分析，例如残差分析。

扩展卡尔曼滤波(Extended Kalman Filter,EKF)

卡尔曼滤波KF要求被控系统为线性系统，但实际系统往往不是线性系统，因此需要考虑如何将卡尔曼滤波应用到非线性系统中。扩展卡尔曼滤波EKF可以用于解决非线性系统的卡尔曼滤波，假设系统模型为
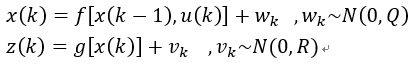
在这里插入图片描述
EKF的思想是在将系统模型进行Taylor展开，只保留到一阶项得到线性系统。但是在计算先验估计值和估计测量值时，仍用非原系统，即

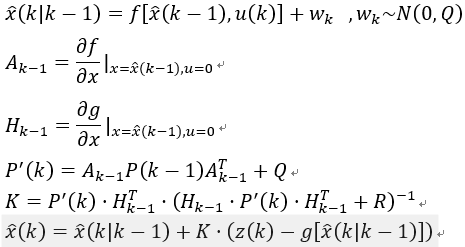
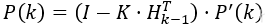
转自-卡尔曼滤波算法