本文主要是介绍CGAL的多面体凸分解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1、介绍
对于许多非凸多面体的应用,有高效的解决方案,这些解决方案首先将多面体分解为凸块。例如,可以通过将两个多面体分解为凸块来计算两个多面体的Minkowski和,然后计算凸块的配对Minkowski和,并将配对和结合起来。
虽然将多面体分解成尽可能少的部分是可取的,但这个问题是NP-hard的。我们的实现将Nef多面体N分解为O(r^2)个凸块,其中r是与多面体内部成大于180度的角的两个相邻面的边数。这些边也被称为反射边。O(r^2)个凸块的上界是最坏情况下的最优解。
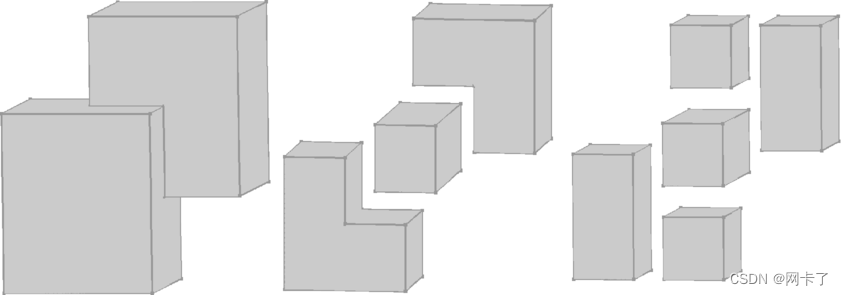
基于垂直面的插入进行垂直分解(从顶部看)。左图:非凸多面体。中图:非垂直反射边已解决。右图:垂直反射边已解决。子体积是凸的。
我们的分解分为两个步骤。在第一步中,通过插入垂直面来解析每个非垂直反射边e。在第二步中,我们对垂直反射边做同样的处理。上图说明了这两个步骤。
目前,我们的实现仅限于对有界多面体的分解。我们计划扩展到无界多面体。
2、接口和使用
Nef_polyhedron_3的实例代表三维空间到顶点、边、面和体积的细分。其中一些项目形成了多面体(已选择),而其他项目则表示多面体外围的体积或空洞(未选择)。例如,单位立方体是点集[0,1]3。表示单位立方体的最小细分有8个顶点,12条边,6个面和2个体积。由顶点、边和面围成的体积是立方体的内部,因此已选择。立方体外的体积不属于它,因此未选择。顶点、边和面(也称为边界项)是分隔两个体积所必需的,但也有助于表示拓扑属性。对于封闭的单位立方体,边界项是多面体的部分,因此已选择,但对于开放单位立方体[0,1)3,它们未被选择。每个项目都有自己的选择标记,这允许在布尔和拓扑操作下正确表示Nef多面体。
通常,Nef_polyhedron_3的实例不包含任何冗余项。但是,convex_decomposition_3()通过选定的面将给定Nef_polyhedron_3的选定体积进行细分。因此,这些额外的面是冗余的,即它们的插入改变了多面体的表示形式,但不影响多面体本身。
当convex_decomposition_3()解决所有反射边时,已选择的子体积变得凸起。每个子体积由一个单独的体积项表示,因此可以像第Shells部分的描述那样单独遍历。另一种访问凸块的方法是将它们转换为单独的Nef多面体,如以下示例代码所示。
注意,由于对有界多面体的限制,扩展核的使用是不必要的,而且代价高昂。因此,我们不支持在凸分解中使用扩展核。
3、其他
CGAL的Nef_polyhedron_3和Polyhedron_3都是表示三维形状的数据结构,但它们在某些方面存在显著差异。
Nef_polyhedron_3:Nef_polyhedron_3是CGAL库中表示非扩展Nef三维多面体的类。Nef多面体是封闭的,无空洞的多面体,其所有顶点、边和面都位于多面体的边界上。Nef多面体满足一些特定的性质,例如它们是不可压缩的,即不可能通过连续变形(例如挤压或拉伸)来改变其形状而不破坏它。Nef_polyhedron_3特别适用于处理那些需要考虑到拓扑和几何信息的情况,例如布尔运算、碰撞检测等。
Polyhedron_3:Polyhedron_3是表示任意三维多面体的类。它允许多面体有孔洞,即可以有内部的顶点、边和面。与Nef_polyhedron_3相比,Polyhedron_3提供了更一般的多面体表示。它对于需要表示更广泛类型对象的情况更为合适,如模拟、几何建模等。由于其更一般的性质,与Nef_polyhedron_3相比,Polyhedron_3在某些操作上可能效率较低。
总结:如果你需要处理封闭、无空洞的多面体,并关心其拓扑性质,那么Nef_polyhedron_3可能是一个更好的选择。如果你需要处理更一般的多面体,或者需要表示有孔洞的多面体,那么Polyhedron_3可能更适合你的需求。
CGAL 5.6 - Convex Decomposition of Polyhedra: User Manual
这篇关于CGAL的多面体凸分解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






