【洛谷P1198】最大数【分块】

本文主要是介绍【洛谷P1198】最大数【分块】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目大意：

题目链接：https://www.luogu.org/problemnew/show/P1198
现在请求你维护一个数列，要求提供以下两种操作：

1. 查询操作。
   语法：$QL$
   功能：查询当前数列中末尾L个数中的最大的数，并输出这个数的值。
   限制：$L$不超过当前数列的长度。$(L>0)$
2. 插入操作。
   语法：$An$
   功能：将$n$加上$t$，其中$t$是最近一次查询操作的答案（如果还未执行过查询操作，则$t=0$)，并将所得结果对一个固定的常数$D$取模，将所得答案插入到数列的末尾。
   限制：$n$是整数（可能为负数）并且在长整范围内。

注意：初始时数列是空的，没有一个数。

---

思路：

$M\le 200000$
分块啊。
由于确定了最终数字不会超过$2\times 10^5$，所以就可以直接确定分成$\sqrt{2\times 10^5}$个块，使用计算器得

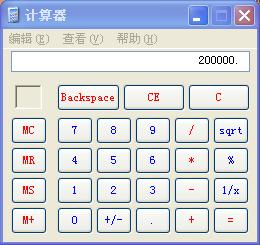
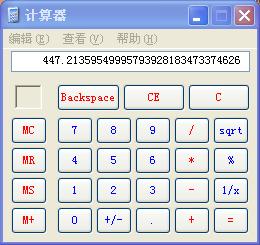
那就将一个块设置成$448$就好了。
对于一个插入操作，判断是否需要建立一个新的块。然后将数据储存进去。
对于一个查询操作，按照朴素的分块求法求$[n-x+1,n)$的最大值即可。

---

代码:

#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;const int N=200010;
const int T=448;
int n,m,MOD,x,t,a[N],L[T],R[T],maxn[T],pos[N],ans;
char c;int find_max(int l,int r)  //暴力求l到r的最大值
{int Maxn=-2147483648;for (int i=l;i<=r;i++)Maxn=max(Maxn,a[i]);return Maxn;
}int ask(int l,int r)
{int q=pos[l],p=pos[r];if (q==p) return ans=find_max(l,r);  //直接暴力求int Maxn=max(find_max(l,R[q]),find_max(L[p],r));  //两边暴力求for (int i=q+1;i<p;i++)Maxn=max(Maxn,maxn[i]);return ans=Maxn;
}int main()
{scanf("%d%d",&m,&MOD);while (m--){c=getchar();while (c!='A'&&c!='Q') c=getchar();scanf("%d",&x);if (c=='A'){a[++n]=(int)(((ll)x+(ll)ans)%MOD);  //此处会炸int，切记用long long！if (n%T==1)  //建立新块{t++;L[t]=R[t]=R[t-1]+1;}else R[t]++;pos[n]=t;maxn[t]=max(maxn[t],a[n]);}else printf("%d\n",ask(n-x+1,n));}return 0;
}

---

题外话

$$论随意使用cin的后果$$

这篇关于【洛谷P1198】最大数【分块】的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---