文章解读与仿真程序复现思路——电网技术EI\CSCD\北大核心《基于混合博弈的配电网与多综合能源微网优化运行》

本文主要是介绍文章解读与仿真程序复现思路——电网技术EI\CSCD\北大核心《基于混合博弈的配电网与多综合能源微网优化运行》，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本专栏栏目提供文章与程序复现思路，具体已有的论文与论文源程序可翻阅本博主免费的专栏栏目《论文与完整程序》

这个标题涉及到配电网和多综合能源微网的优化运行，而优化的方法基于混合博弈理论。让我们逐步解读这个标题的关键部分：

基于混合博弈的： 指出这项研究采用了混合博弈理论作为优化方法的基础。混合博弈是博弈论的一个分支，涉及多个参与者，每个参与者可能有不同的信息和策略，这样的博弈模型可以用来解决复杂系统中的决策问题。
配电网与多综合能源微网： 指出研究的焦点是配电网和多综合能源微网。配电网是指用于将电能从发电站输送到终端用户的网络，而多综合能源微网则可能包括多种能源资源（如太阳能、风能、储能等）和相应的微网系统，这些系统在一定范围内可以独立运行或与主电网连接。
优化运行： 强调研究的目标是通过优化方法来改善配电网和多综合能源微网的运行。这可能包括最大化能源利用效率、降低运行成本、提高系统可靠性等方面的目标。

综合起来，这个标题表明研究的重点是通过应用混合博弈理论，对配电网和多综合能源微网进行优化运行的探讨。这种研究可能有助于提高能源系统的智能化、灵活性和可持续性。

摘要：该文研究了同一配电网下的多个综合能源微网(integrated energy microgrids,IEM)的协同管理问题，旨在通过配电网运营商(distribution system operator,DSO)制定电能价格以协调IEM联盟的机组调度、需求响应和成员间的点对点(peer-to-peer,P2P)电能交易。首先，构建了DSO与IEM联盟能源交易框架，分析了DSO与IEM联盟的博弈关系。其次，将主从博弈与合作博弈相结合，建立了DSO与IEM联盟混合博弈优化模型，其中DSO为领导者，以最大化自身效益为目标，通过制定电能价格引导IEM联盟运行优化；IEM联盟为跟随者，以最大化自身效益为目标，通过合作对DSO的决策进行响应。基于纳什谈判理论，将IEM模型等效为联盟效益最大化和合作收益分配2个子问题，以保证IEM联盟的合作收益能在联盟成员之间公平分配。最后，利用二分法分布式优化算法结合交替方向乘子法(alternating direction multiplier method,ADMM)求解所构建的模型。结果表明，该文提出的混合博弈模型有效协调了IEM联盟的运行优化，并实现了IEM联盟成员合作收益的公平分配。

这篇文章的摘要主要涉及到同一配电网下多个综合能源微网（IEM）的协同管理问题，以及通过配电网运营商（DSO）制定电能价格来协调IEM联盟的运营。以下是摘要的主要内容解读：

研究背景： 文章研究了同一配电网下的多个IEM的协同管理问题。IEM是指综合能源微网，可能包括多种能源资源和相应的微网系统。
目标： 研究的目标是通过DSO制定电能价格，协调IEM联盟的机组调度、需求响应和成员间的P2P电能交易。
建模过程：
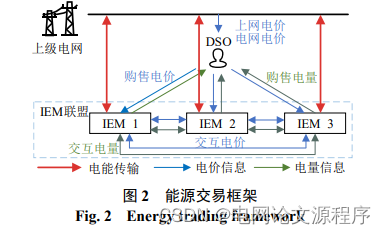
- 能源交易框架构建： 首先，构建了DSO与IEM联盟的能源交易框架，同时分析了DSO与IEM联盟之间的博弈关系。
- 混合博弈优化模型： 将主从博弈与合作博弈相结合，建立了DSO与IEM联盟的混合博弈优化模型。在这个模型中，DSO作为领导者，以最大化自身效益为目标，通过制定电能价格引导IEM联盟的运行优化；而IEM联盟作为跟随者，以最大化自身效益为目标，通过合作对DSO的决策进行响应。
理论基础： 该模型基于纳什谈判理论，将IEM模型等效为联盟效益最大化和合作收益分配两个子问题，以确保IEM联盟的合作收益在成员之间公平分配。
求解方法： 为了解决建立的混合博弈优化模型，作者采用了二分法分布式优化算法结合ADMM。这是一种分布式求解方法，用于处理博弈理论中的优化问题。
结果： 文章的最后指出，提出的混合博弈模型有效协调了IEM联盟的运行优化，并成功实现了IEM联盟成员之间合作收益的公平分配。

总体而言，这项研究致力于解决配电网下多个综合能源微网的协同管理问题，通过博弈理论和混合博弈优化模型，实现DSO和IEM联盟之间的协调与合作。

关键词：混合博弈;纳什谈判;点对点电能交易;电力市场;需求响应;综合能源微网联盟;

解读关键词：

混合博弈（Mixed Game）： 这指的是一种博弈理论中的概念，可能表示在模型中同时存在多种博弈策略或类型。在文章中，混合博弈可能是指同时考虑了主从博弈和合作博弈的优化模型。
纳什谈判（Nash Bargaining）： 这是博弈论中的一个概念，指的是一种合作博弈的解决方案，其中各方通过协商分配资源，以达到对彼此都是最好的结果。在文章中，可能涉及将IEM模型等效为联盟效益最大化和合作收益分配的纳什谈判理论。
点对点电能交易（Peer-to-Peer Electricity Trading）： 这指的是能源交易中直接发生在两个节点之间的交易，而不是通过中介机构。在文章中，可能是IEM联盟成员之间进行的直接电能交易的一部分。
电力市场（Electricity Market）： 这可能涉及到文章讨论的电力市场的方方面面，包括电能价格的制定、市场运营商的角色等。
需求响应（Demand Response）： 这表示在电力系统中，用户根据市场价格或系统需求的变化，调整其电力使用的能力。在文章中，可能是DSO通过电能价格引导IEM联盟成员进行的一种操作手段。
综合能源微网联盟（Integrated Energy Microgrid Alliance）： 这可能是指多个综合能源微网（IEM）组成的联盟，共同面对电力市场和运营商的管理。在文章中，可能讨论了联盟成员之间的合作和协调问题。

这些关键词共同描绘了文章的研究范围和方法，涉及了博弈理论、电力市场、点对点电能交易等多个方面，旨在解决综合能源微网联盟中的协同管理问题。

仿真算例：

本章节通过算例仿真验证所提模型的合理性。参考文献[8,18]设置仿真参数，模型所用到的参数列于附录 E 中，电网电价与上网电价如表 1 所示， IEM 冷热负荷和新能源出力如附图 E1—E2 所示。DSO 与 IEM 相关参数如附表 E1—E2 所示，二分法收敛系数设为 0.01，ADMM 收敛系数设为 0.001。算例仿真通过 Matlab 平台使用 Yalmip 调用 Cplex 与 Mosek 求解器，利用二分法分布式优化算法结合 ADMM 求解模型。二分法的迭代收敛情况与结果对比请见附图 E3，ADMM 的迭代收敛情况请见附图 E4。为证明本文方法的有效性，设立以下不同方案进行对比分析，不同方案下的运行结果如表 2 所示，合作前后效益对比如表 3 所示。方案一：考虑 DSO 与 IEM 联盟之间的主从博弈，考虑 IEM 联盟成员间的合作博弈，考虑需求侧响应，即本文所提方法。方案二：考虑 DSO 与 IEM 联盟之间的主从博弈，不考虑 IEM 联盟成员间的合作博弈，考虑需求侧响应。方案三：考虑 DSO 与 IEM 联盟之间的主从博弈，考虑 IEM 联盟成员间的合作博弈，不考虑需求侧响应。

仿真程序复现思路：

要复现该仿真，首先需要了解模型中使用的算法和参数。根据描述，该仿真使用了Matlab平台、Yalmip工具箱以及Cplex和Mosek求解器。以下是复现思路的概要，以及使用Matlab编写的示例代码：

% 设置仿真参数
convergence_coefficient_bisection = 0.01;
convergence_coefficient_admm = 0.001;
% 其他参数设置...% 调用Cplex求解器
solver_cplex = 'cplex';
ops_cplex = sdpsettings('solver', solver_cplex);% 调用Mosek求解器
solver_mosek = 'mosek';
ops_mosek = sdpsettings('solver', solver_mosek);% 初始化模型参数
% 初始化电网电价、上网电价、DSO与IEM相关参数等...% 仿真过程
% 迭代次数
num_iterations_bisection = 100;
num_iterations_admm = 50;% 初始化变量
% 初始化二分法和ADMM的变量...% 二分法迭代
for iter_bisection = 1:num_iterations_bisection% 二分法迭代过程...% 更新变量...% 判断收敛条件if convergence_condition_bisection < convergence_coefficient_bisectionbreak;end
end% ADMM迭代
for iter_admm = 1:num_iterations_admm% ADMM迭代过程...% 更新变量...% 判断收敛条件if convergence_condition_admm < convergence_coefficient_admmbreak;end
end% 保存仿真结果
% 保存迭代收敛情况和最终结果...% 绘制迭代收敛图
figure;
% 绘制迭代收敛情况...% 分析结果并输出表格
% 分析结果...% 方案对比
% 方案一
% 方案二
% 方案三
% 对比分析...% 结果展示
disp('仿真结果:');
disp('迭代收敛情况:');
% 显示迭代收敛情况...
disp('最终结果:');
% 显示最终结果...

请注意，以上代码是一个简化的框架，具体实现需要根据您的模型和算法的细节进行调整。确保您理解模型的数学描述以及仿真过程中的计算步骤，并将其转化为相应的Matlab代码。

这篇关于文章解读与仿真程序复现思路——电网技术EI\CSCD\北大核心《基于混合博弈的配电网与多综合能源微网优化运行》的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！