算法上机（三） 动态规划解决装配线排程（调度）问题

问题描述

一汽车厂有两条装配线，每条装 配线有n个工序站台，每条装配线的 第j个站台的功能相同,但是效率不一致，每条装配线的上线和下线时间表示为e1，e2和x1，x2。另外，切换线路也需要时间t1j，t2j。求如何充分利用两条装配线, 使得组装一辆汽车的时间短。
如图所示

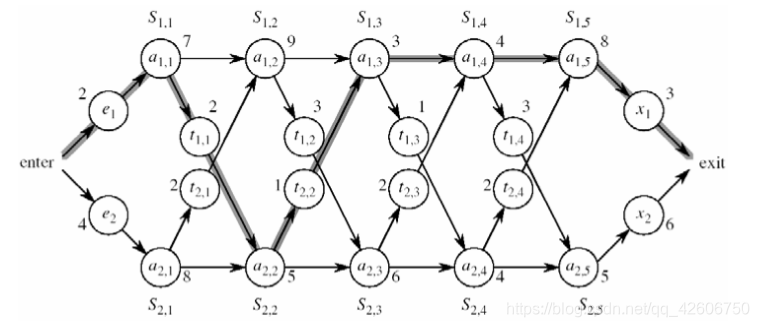
解决方法

这里介绍两种方法。第一，蛮力法。简单易懂，时间复杂度高，不推荐。第二，动态规划法。比较难理解，但效率高。

蛮力法

用迭代的方法计算装配线排程 所有可能的组合情况，比较并选择出短时间的组合。由于每个站有两种可能，因此总共有2的n次方种可能，时间复杂度也为O(2^n)。

动态规划法

自底向上求解最优解。先求出到第i个站的最优解，再根据此求出第i+1个站的，直到第n个站，以及下线完成生产。有：f1[i] = min(f1[i-1]+a1[i],f2[i-1]+t2[i-1]+a1[i]）。
其中，f1[i]表示在第一条线完成第i个站所需要的最短时间，a1[i]表示在第一条线第i个站加工需要的时间，t1[i]表示在第一条线第i个站加工完成后转到第二条线需要的时间。
代码如下。

#include <stdio.h>
#include <stdlib.h>const int n = 5;	//每条线工作站的数目 
int a1[n] = {7,9,3,4,8};	//元件在第一条线第i个站加工需要的时间 
int a2[n] = {8,5,6,4,5};
int e1=2,e2=4,x1=3,x2=6;	//e起始入线时间，x终止出线时间 
int t1[n-1] = {2,3,1,3};	//在第i个站换线需要的时间 
int t2[n-1] = {2,1,2,2};
int f1[n],f2[n];	// 动态规划，存储到第i个站的最短时间 
int l[2][n];	//存储路径 
int f,last;		//最终时间和路径 void fatestway(){f1[0] = e1+a1[0];l[0][0] =1;f2[0] = e2+a2[0];l[1][0] = 2;printf("%d,%d\n",f1[0],f2[0]);for(int i=1;i<n;i++){//f1[i] = min(f1[i-1]+a1[i],f2[i-1]+t2[i-1]+a1[i])if(f1[i-1]+a1[i]<f2[i-1]+t2[i-1]+a1[i]){f1[i] = f1[i-1]+a1[i];l[0][i] = 1;}else{f1[i] = f2[i-1]+t2[i-1]+a1[i];l[0][i] = 2;}//f2[i] = min(f2[i-1]+a2[i],f1[i-1]+t1[i-1]+a2[i])if(f2[i-1]+a2[i]<f1[i-1]+t1[i-1]+a2[i]){f2[i] = f2[i-1]+a2[i];l[1][i] = 2;}else{f2[i] = f1[i-1]+t1[i-1]+a2[i];l[1][i] = 1;}printf("%d,%d\n",f1[i],f2[i]);}if(f1[n-1]+x1<f2[n-1]+x2){f = f1[n-1]+x1;last = 1;}else{f = f2[n-1]+x2;last = 2;}
}
//递归调用，逆序打印出每个站在哪条线路 
void print(int i,int j){if(j==1){printf("Line:%d Station:%d\n",i,j);}else{print(l[i-1][j-1],j-1);printf("Line:%d Station:%d\n",i,j);}
}int main (void){fatestway();print(last,n);printf("总路线时间：%d",f);
}