GAMES104-现代游戏引擎：从入门到实践 - 物理引擎课程笔记汇总

本文主要是介绍GAMES104-现代游戏引擎：从入门到实践 - 物理引擎课程笔记汇总，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

0 入门资料

• GAMES104-现代游戏引擎：从入门到实践_课程视频_bilibili
• GAMES104官方账号 - 知乎
• 课程主页
• 课程小引擎Piccolo
• 课件：
  • GAMES104_Lecture10_Physics System_Basic Concepts.pdf
  • GAMES104_Lecture11_Physics System_Applications.pdf

1 物理引擎

• 物理引擎的用途：
  • 碰撞检测
  • 解决碰撞、其它约束限制
  • 更新所有物体的世界坐标（world Transform）

基本概念

Actor & shapes

Actor

• 静态 static actor：不会移动，阻碍你
• 动态 dynamics actor：符合动力学原理，可以被 forces、torque、impulse影响
• 触发器 trigger
• kinematic actor：可以违背物理学，让它按照设计的运动

Actor Shapes

• 求交点

Shapes	图例	备注
Spheres 球体
Capsules 胶囊体		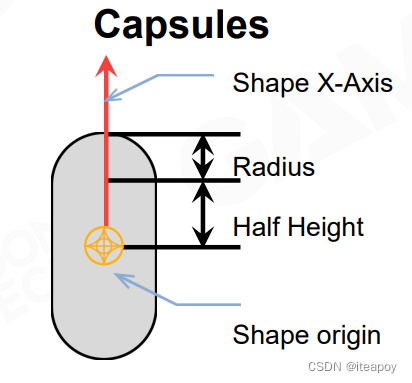- 人体
Boxes 盒子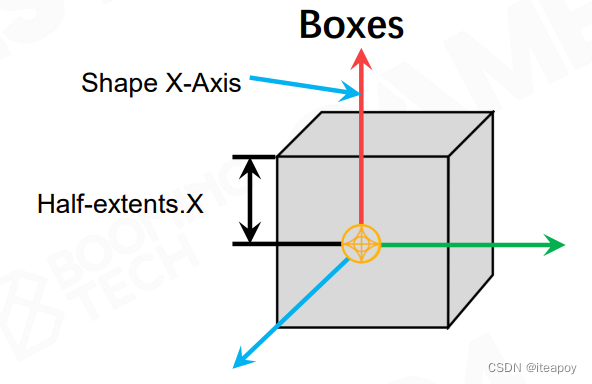
Triangle Meshes 三角		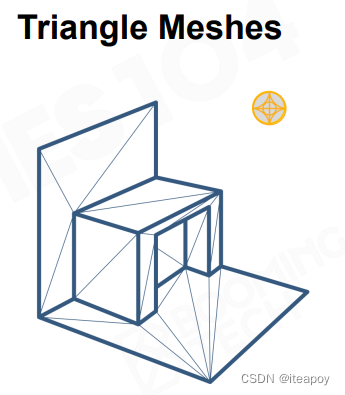- 必须是密闭的 - Dynamic actors 不能使用
Height Fields		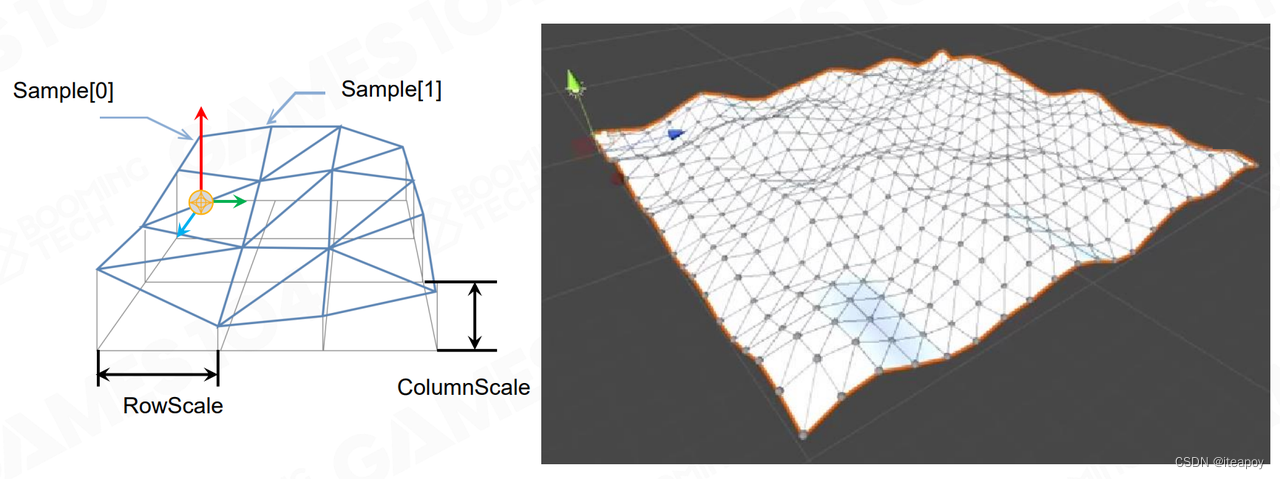- 用于地形

Shape 的属性

• 质量/密度 Mass and Density
• 质心 Center of Mass
• 摩擦力/弹性 Friction & Restitution ：受到物理材质的影响
• 力 Forces：常见的力包括拉力、重力、摩擦力
• 冲力/冲量 impulse：例如爆炸
• 移动 movement

半隐式欧拉积分

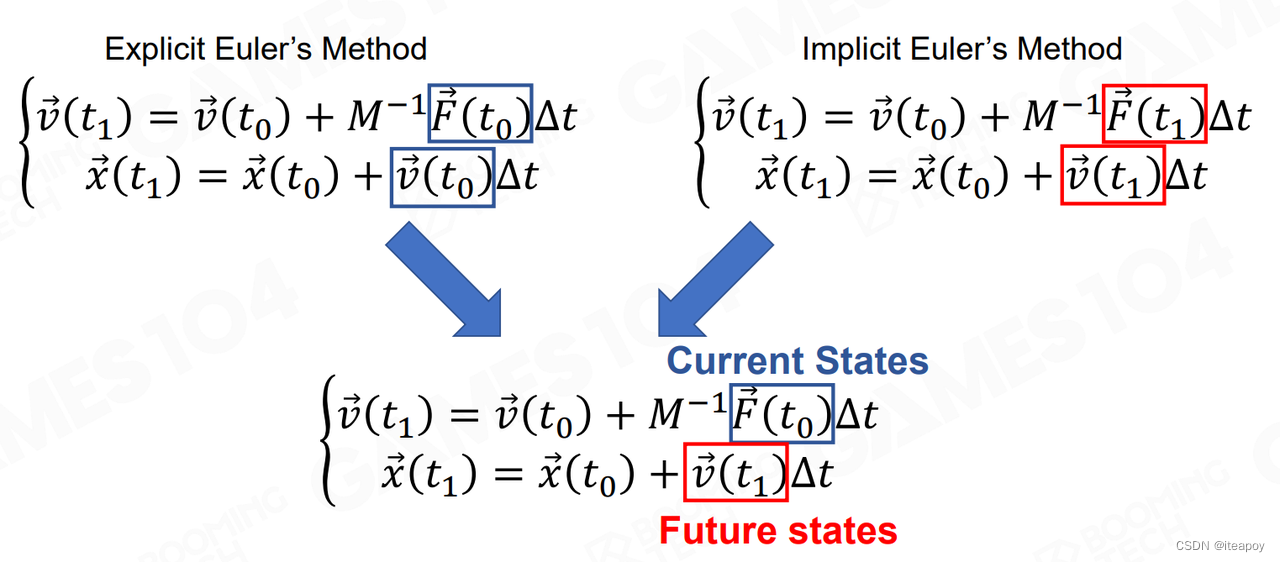
• 【优点】
  • 容易模拟
  • 较稳定
• 【缺点】
  • 实际消耗时间比真实时间要久一点

Rigid body dynamics

粒子动力学 Particle Dynamics	刚体动力学 Rigid body Dynamics
位置 Position $$\vec{x}$$	旋转 Orientation $$\mathbf{R}$$
线速度 Linear Velocity $$\vec{v}=\frac{\mathrm{d}\vec{x}}{\mathrm{d}t}$$	角速度 Angular velocity $$\vec{\omega }=\frac{\vec{v}\times \vec{r}}{|\vec{r}{|}^2}$$
加速度 Acceleration $$\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=\frac{d^2\vec{x}}{d{t}^2}$$	角加速度 Angular acceleration $$\vec{\alpha }=\frac{\mathrm{d}\vec{\omega }}{\mathrm{d}t}=\frac{\vec{a}\times \vec{r}}{|\vec{r}{|}^2}$$
质心 Mass $$M=\sum m_i$$	转动惯量 Inertia tensor $$\mathbf{I}=\mathbf{R}\cdot {\mathbf{I}}_0\cdot {\mathbf{R}}^{\mathrm{T}}$$
动量 Momentum $$\vec{p}=M\vec{v}$$	角动量 Angular momentum $$\vec{L}=\mathbf{I}\vec{\omega }$$
力 Force $$\vec{F}=\frac{d\vec{p}}{dt}=m\vec{a}$$	力矩 Torque $$\vec{\tau }=\frac{d\vec{L}}{dt}$$

Collision Detection

• 碰撞检测：东西是否撞上了

碰撞检测的两个阶段		方法
粗筛	1. 直接用AABB找到相交的刚体 2. 找到潜在的重叠刚体对	1. BVH Tree 2. Sort and Sweep
细筛	1. 进一步检测重叠 2. 得到相交信息 1. 相交点 2. 相交法线 3. 穿透深度	1. Basic Shape Intersection Test 2. MinkowskiDifference-based Methods 3. Separating Axis Theorem

1. Basic Shape Intersection Test

圆与圆碰撞	圆与胶囊体碰撞	胶囊体与胶囊体碰撞

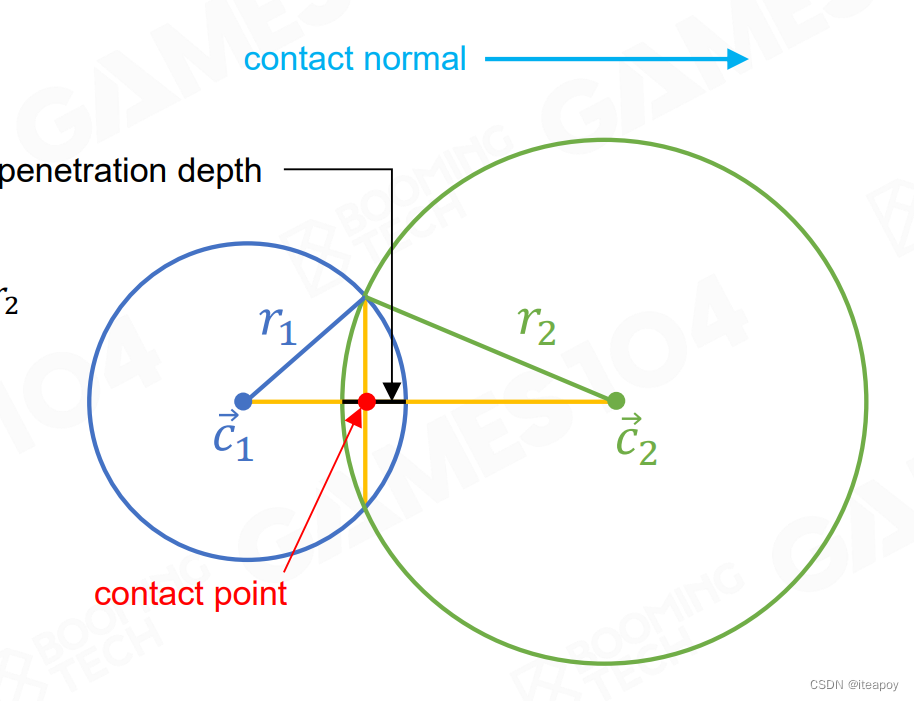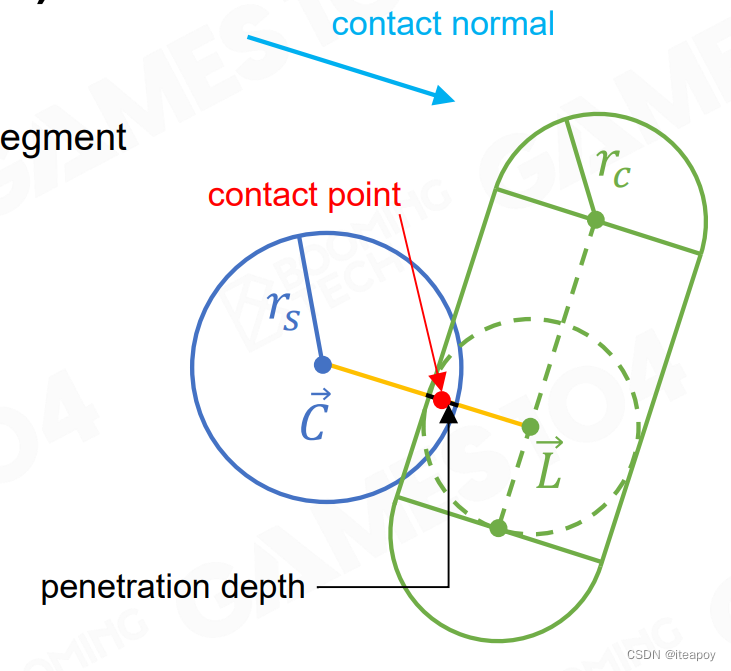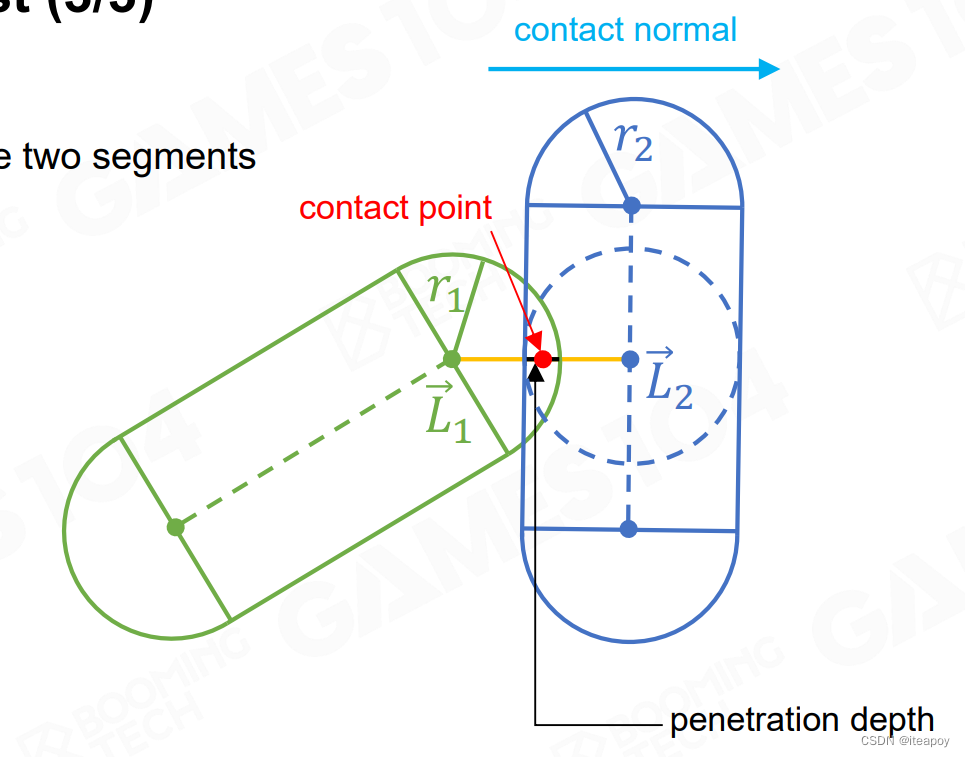2. MinkowskiDifference-based Methods

碰撞	未碰撞

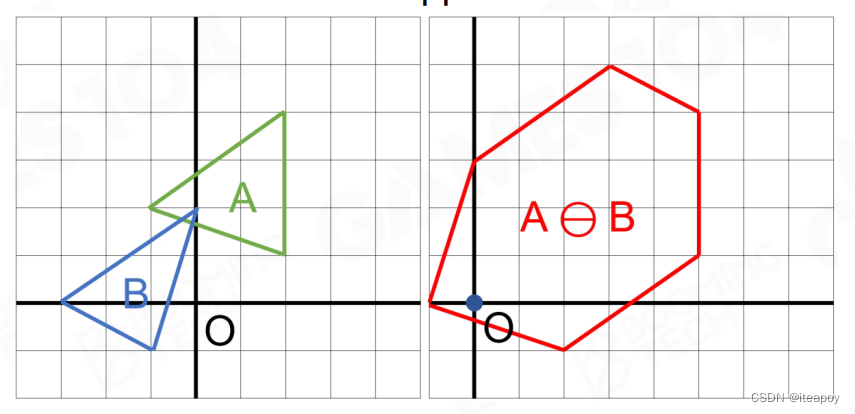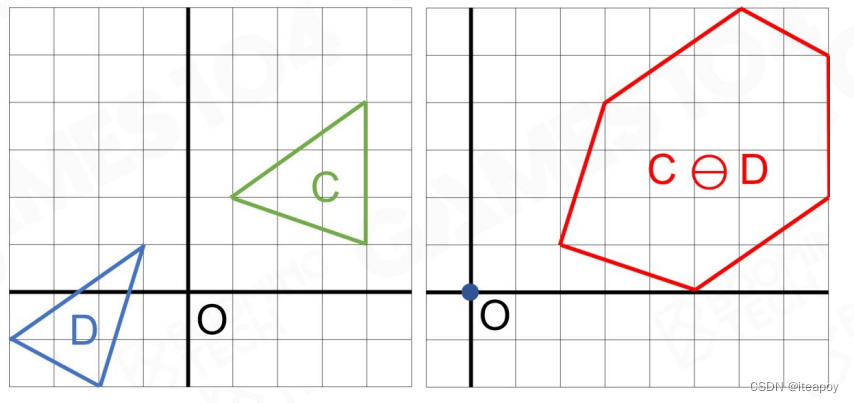3. Separating Axis Theorem（SAT）

• 一定能找到一根轴，分离两个凸包

	碰撞	不碰撞
2D 情况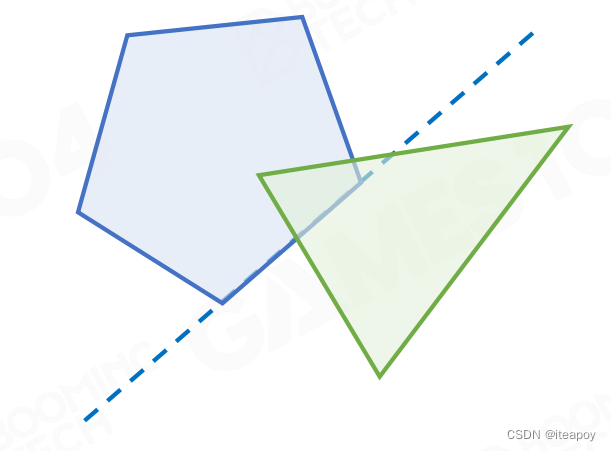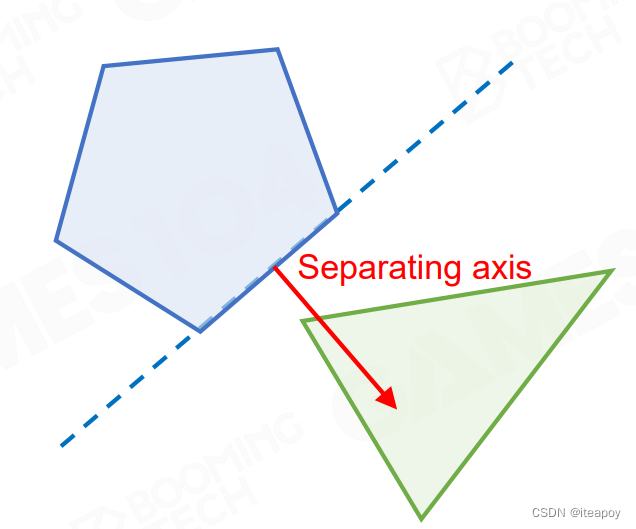
3D 情况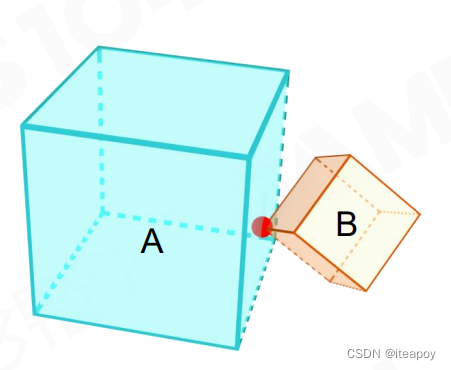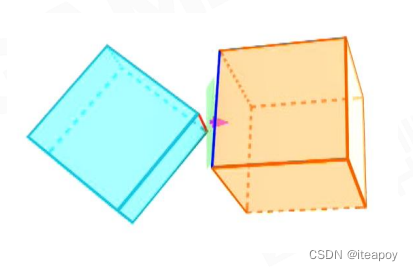

• 连续碰撞检测 Continuous Collision Detection（CCD）

Collision Resolution

• 如何处理碰撞？分离

	方法	具体方法
	加入Penalty Force分离	加一个反向的惩罚力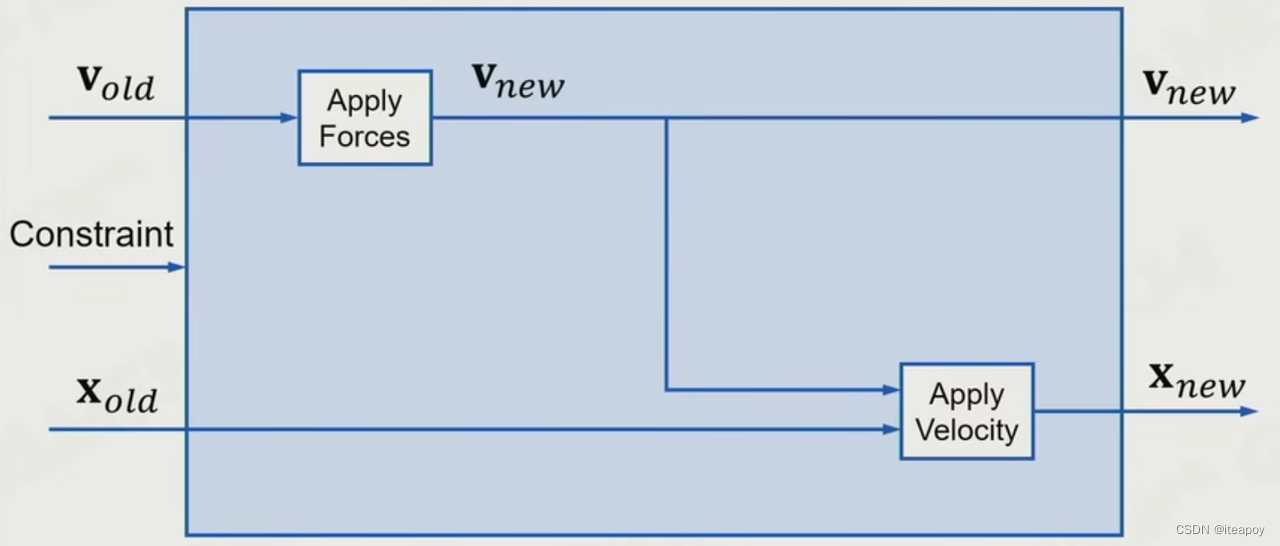
转为约束问题	解决速度约束	不断尝试给一个冲量
	解决位置约束	见 ragdoll - joint constraints

应用与实践

Character controller

• 反物理的系统：摩擦力无穷大
• 用 Kinematic Actor
  • 不受物理规则影响
  • 推动别的物体
• 形状
  • 双层胶囊
• Sweep test
  • 与物体碰撞后，往旁边平移
• Stepping 爬楼梯
  • 尝试往上提，再往前走

Ragdoll

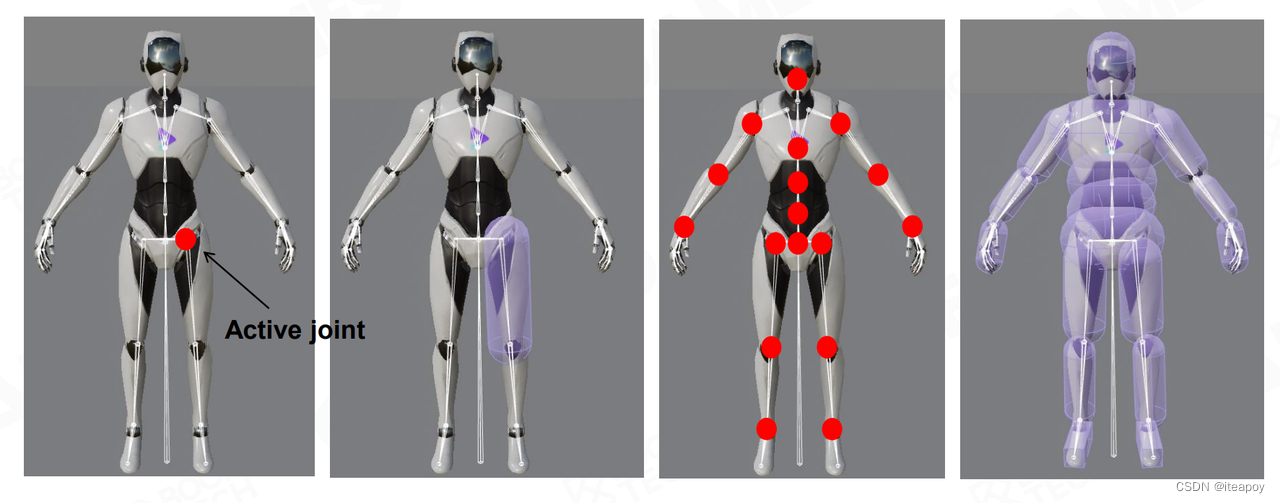
• 人体的 joint 约束（joint constraints）

Hinge 铰链	Ball-and-socket 球窝	Pivot 枢轴	Saddle 鞍状	Condyloid 髁状突	Gliding 滑行

这篇关于GAMES104-现代游戏引擎：从入门到实践 - 物理引擎课程笔记汇总的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---