流体力学基础 | 用于求解雷诺应力的湍流模式

本文主要是介绍流体力学基础 | 用于求解雷诺应力的湍流模式，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1 背景

2 布辛涅斯克（Boussinesq）涡粘性假设

3 零方程模型（代数方程模型）

4 一方程紊流模型

4.1 方程建立

4.2 方程模化

5 k-ε双方程紊流模型

6 总结

1 背景

在前面的文章中我们写道，为了一定程度上描述湍流的平均流动性质，我们从N-S方程进行雷诺平均我们得到了雷诺时均方程RANS方程。对不可压缩流体，直角坐标系下的RANS方程为：

$\rho \frac{\partial{\overline{u_i}}}{\partial{t}} + \rho u_j \frac{\partial{\overline{u_i}}}{\partial{x_j}} = \rho \overline{f_i} - \frac{\partial{\overline{p}}}{\partial{x_i}} + \frac{\partial}{\partial x_j}(\mu \frac{\partial\overline{u_i}}{\partial x_j} - \rho \overline{u_i'u_j'})$

雷诺应力代表了紊流脉动运动对时均流动的影响。由于雷诺应力的出现，增加了六个未知量，使得原来封闭的流体运动方程组在平均化后不再封闭。因此，针对雷诺方程中的雷诺应力，需要构造有关雷诺应力的新的方程封闭RANS方程组。下面我们分别介绍主要采用的几种，零方程、一方程和二方程模式。

2 布辛涅斯克（Boussinesq）涡粘性假设

类似于层流分子粘性切应力的广义牛顿内摩擦定律，布辛涅斯克假定紊流雷诺应力也与平均场的速度梯度存在比例关系：

$-\rho \overline{u_i'u_j'} = -\frac{2}{3}\rho k \delta_{ij} + \rho \upsilon _t(\frac{\partial{\overline{u_i}}}{\partial{x_j}} +\frac{\partial{\overline{u_j}}}{\partial{x_i}} )$

其中 k 为紊动能，δij为克罗内克记号，γt为紊动涡粘系数。与流体分子粘性系数γ的差别是，γ是流体的分子微观物质属性，与流动本身无关；而γt则为紊流运动宏观特性，与紊流时均速度场及其边界形状有密切关系。

在布辛涅斯克假设的基础上，紊流模式理论的任务就是给出涡粘性系数γt的具体计算方法。

零方程模式（代数模型）

在涡粘性模式的框架下，零方程涡粘性模型包括：

① γt为常数的模型；

②普朗特半经验混合掺长模型。

零方程模式的共同特点是不需要求解新的微分输运方程。

一方程模型

需要求解一个微分方程。

双方程模型

需要求解两个微分方程。

3 零方程模型（代数方程模型）

该模式使用最多的是普朗特假说和混合长度理论。

类比于气体分子的平均自由程，假设流体微团在运行某一距离后才与周围其他流体掺混，失去其原有的流动特征，而在运行过程中保持其原有特征不变。

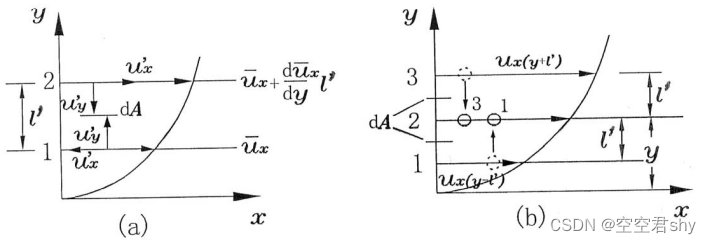
上图所示为二维平行剪切紊流，对该流动根据布辛涅斯克假设，紊动切应力和平均场速度梯度的关系为：

$\overline{u_x} = \overline {u} _x (y), \overline{u}_y = \overline{u}_z = 0\\ \tau_t = -\rho \overline{u_x'u_y'} = \rho \upsilon _t \frac{\partial{ \overline{u}_x}}{\partial{y}}$

因此，我们只需要给出涡粘性系数γt的变化规律，即可封闭方程组。

如上图（b）所示，受脉动影响，在流层1处有一流体质点并可能向上运动一个微小距离到另一流层，如运动到中间流层2.同理，受脉动影响，在流层3处有一流体质点也可能向下运动到一个微小距离到中间流层2。其中l‘假定为气体分子的平均自由行程。

现设坐标为y的中间流层2上的速度为ux(y),坐标为y-l'的；流层1上的速度为ux(y-l') ,坐标为y+l'的流层3上的速度为ux(y+l')。流层1和3与中间流层2的速度差为

$\Delta u_{x1} = \overline{u_x} {(y)} - \overline {u_x}(y-l')\approx l'\frac{du_x}{dy}$

$\Delta u_{x2} = \overline{u_x} {(y+l')} - \overline {u_x}(y)\approx l'\frac{du_x}{dy}$

$\left | \overline{u_x'} \right | = \frac{1}{2}(\Delta u_{x1} + \Delta u_{x2}) = l' \frac{du_x}{dy}$

$\left | \overline{u_y'} \right | = C_1 \left | \overline{u_x'} \right | = C_1l' \frac{du_x}{dy}$

$\left | \overline{u_x' u_y'} \right | = C_2\left | \overline{u_x'} \right | \cdot \left | \overline{u_x'} \right | = C_1C_2l'^2(\frac{du_x}{dy})^2$

令 $l^2 = C_1C_2l'^2$ ，将l称为混合长度。将该式代入前面紊动切应力的表达式中，则得到：

$\tau_t = -\rho \overline{u_x'u_y'} = \rho \left | \overline{u_x'u_y'}\right | = \rho l^2 \left | \frac{d \overline{u_x}}{dy}\right | \cdot \frac{d \overline{u_x}}{dy}$

$\upsilon _t = l^2 \left | \frac{d \overline{u_x}}{dy} \right |$

其中混合长度l由试验确定，紊流边界层流动试验中得到：

$l = \kappa y, \kappa \approx 0.41$

说明在紊流边界层中，混合长度l与离开壁面的距离y成比例，比例系数称为卡门常数。

4 一方程紊流模型

4.1 方程建立

主要建立涡粘性系数γt与紊动能k的关系

紊流涡粘性系数γt反映了紊流中各种尺度漩涡的输运特性，即紊动质量、动量和能量的扩散特性，这一点也可以从涡粘性系数在雷诺平均方程中的作用看出。因为零方程模式没有充分考虑紊流的主要特征，忽略动量紊流的对流和扩散输运，所以不能适用于复杂紊流的情形，因此必须结合紊流输运的主要特征，提出新的模化γt的方法。

根据量纲分析知，γt的量纲为[L^2/T]，而且各种紊动量的扩散作用主要依靠大尺度涡进行输运，因此，可以用紊流大涡的积分尺度l和特征速度u来表示：

$\upsilon _t \propto l \cdot k^{1/2}$

在该式中加入经验常数C得到：

$\upsilon _t = Cl k^{1/2}$

该式即为著名的Kolmogorov - Prandtl 紊动能与涡粘性关系式

因此，由紊动能k的输运方程结合特征尺度l的代数表达式，例如前述卡门混合长度公式，可组成如下紊流特性方程组

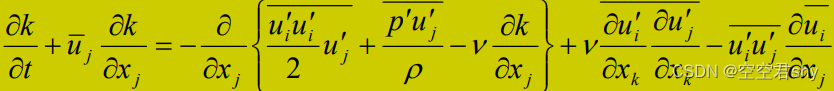
由于在精确的紊动能k方程中，存在未知的扩散项和耗散项，需要做以下近似处理（称为模型化）

4.2 方程模化

1）假定紊动能k的扩散项与k的梯度成正比，即

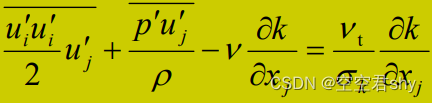
其中γt为涡粘性系数，σk为经验系数，通常取值为1.0左右。

2）小涡的能量耗散率ε等于大尺度涡的能量传输率

其中CD为经验系数，由此简化得到一方程模型中的k方程为

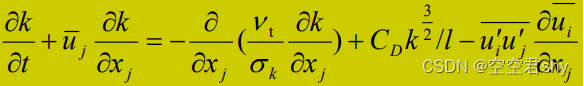
结合普朗特混合长度公式，即可构成以下一方程紊流模型：

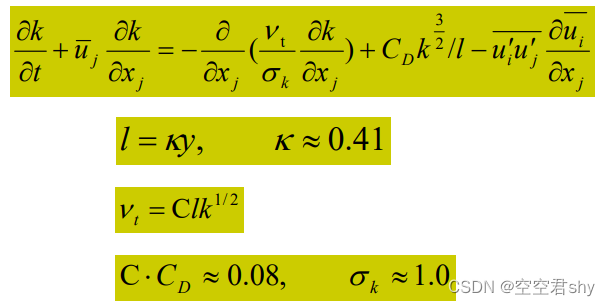
应注意其中C，CD作为经验系数的取值是不独立的。

5 k-ε双方程紊流模型

双方程模式主要寻找涡粘性系数γt与紊动能k和耗散率ε的关系

和前面描述一样，若用紊动能方程求k作为紊流特征速度，而特征尺度l仍然由代数关系表示，例如用混合长度表示，这样得到的雷诺应力封闭模型称为一方程模式。尽管该模型考虑了紊流能量的输运，由于复杂紊流中混合长度的分布很难确定，这使得一方程模型目前为止局限于剪切层（如边界层）流动中。

根据紊流特性可知，紊流特征尺度l和特征速度u（或者k）一样，会受到紊流输运过程的影响和制约。因此，类似于紊动能k方程的形式，需要建立紊流特征尺度l的输运方程描述紊流大尺度涡的对流和扩散作用：对此曾经提出过多种方案，例如分别用过l，kl，k^(1/2)/l、k^(3/2)/2等作为因变量，但结果都不理想。目前应用最广泛的是用耗散率ε代替紊流特征尺度l作为输运方程的因变量，即k-ε双方程紊流模型。

经过模型化后得到模型为：

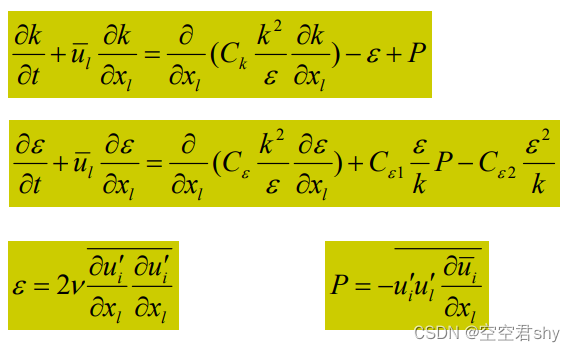
上面的经验常数，是利用格栅后均匀紊流或者均匀剪切紊流的实验结果进行参数率定得到的。

最终我们得到k-ε方程封闭的雷诺平均N-S方程组（RANS）如下

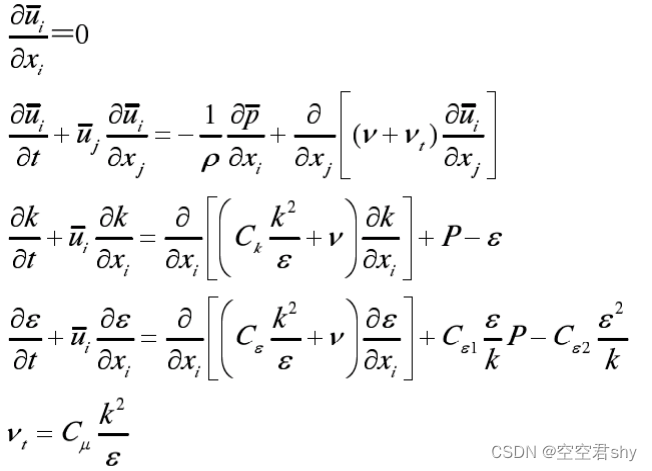
由上方程组可知，共有7个方程，未知数也是7个，因此方程组是封闭的；
以上方程组共有5个经验常数，ε方程就包含了3个，这是因为ε方程几乎每一项都是经过模化得到的，每一个常数都带有一定的随意性，容易引起偏差。要提高k-ε模型模拟水平，提高ε方程的模化质量是关键；
大量的工程应用实践表明，k-ε模型可以计算比较复杂的紊流，比如可以较好预测无浮力的平面射流，平壁面边界层流动，通道流动，喷管内的流动，以及二维和三维无旋流动或弱旋回流流动等。但对边界层分离点附近流动、大曲率流动、非圆截面管道流、明渠流等预测精度差。尽管如此，k-ε模型及其改进形式仍然是当今最广泛应用的紊流模型之一。