线性回归+小批量梯度下降算法

本文主要是介绍线性回归+小批量梯度下降算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.线性模型计算预测值：

线性模型可以看做单层神经网络。
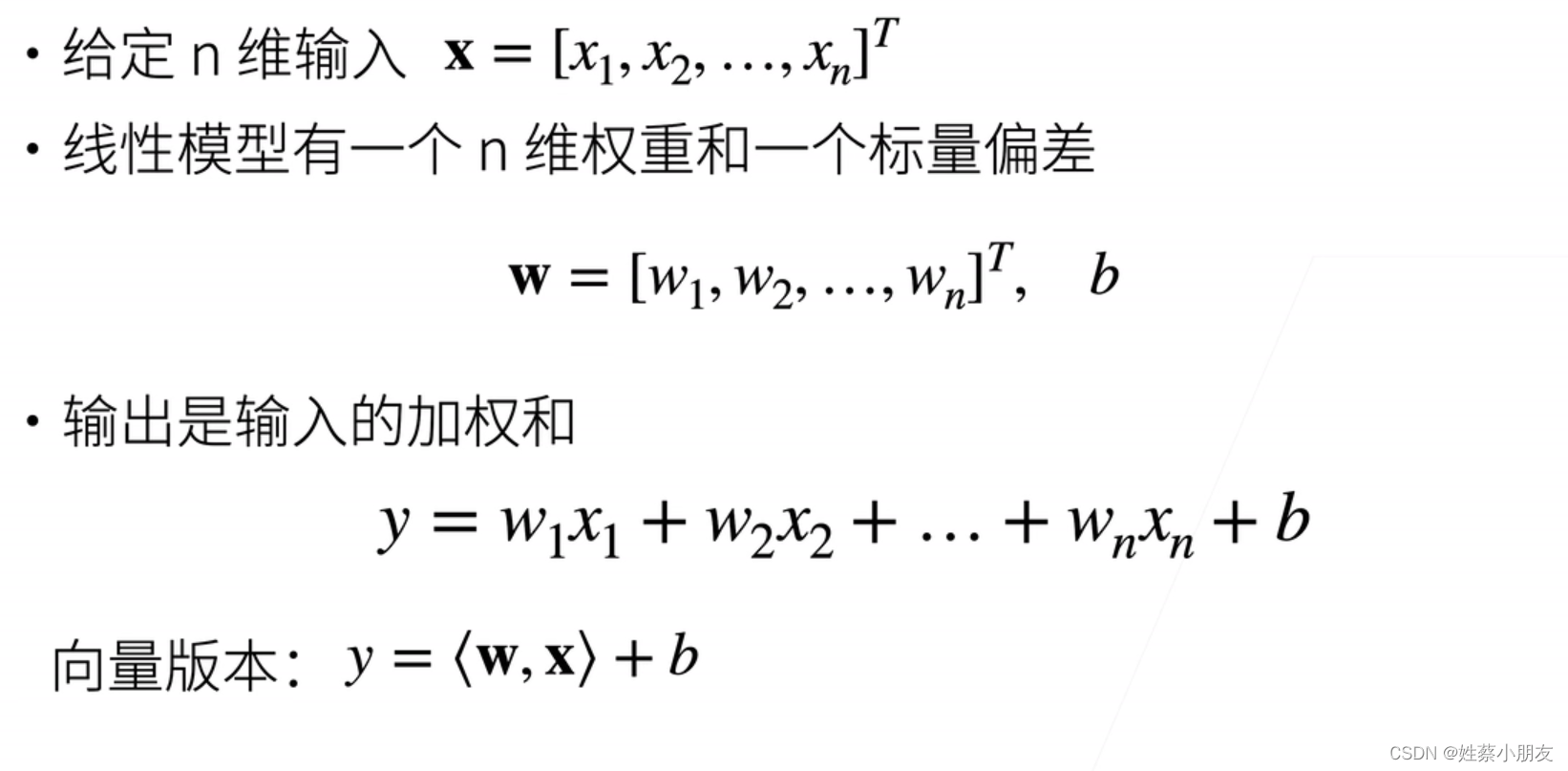
使用线性模型可以对每个样本数据x计算其预测值y
- x为一个样本数据一维向量
- w为权重一维向量，值表示x对应位置所占的权重，未知
- b为偏差值，未知
- y为预测值，即加权平均值

2.使用均方损失作为损失函数：

在这里插入图片描述

平方损失函数可以计算每个样本真实值和预测值之间的差值L
- y为预测值
- y^为真实值
- L为平方差值

3.基础优化算法：梯度下降

在这里插入图片描述

每个圈是一个固定函数值，其中w0为初始函数值
黄线方向是负梯度：函数值沿负梯度方向下降最快
学习率η：沿某个方向走多远距离，太大太小都影响准确率
负梯度×η即沿负梯度方向走η距离
接下来的时刻不断更新wt使其不断接近最优解，即带入平方损失函数后L最小

4.训练数据：

在这里插入图片描述

x为每个样本数据，为一维向量
y为真实值，为数

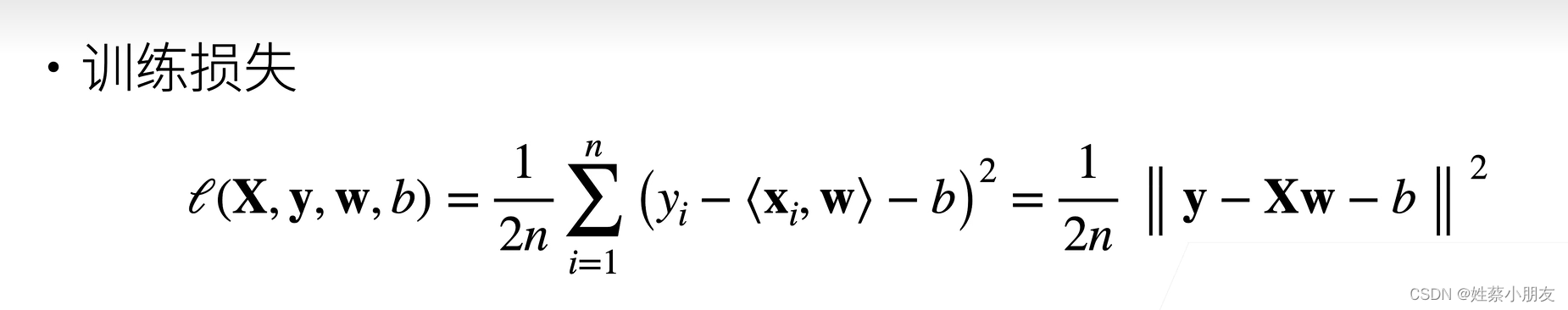
在这里插入图片描述

训练数据的目的是根据优化算法不断更新w、b，根据平方损失函数与真实值y和预测值y^不断计算L，得到的使得L最小的w、b即为w*、b*。
1/2来自损失函数
1/n求均值
对每个样本真实值y减每个样本预测值y^与偏差值b

5.线性回归实现：

%matplotlib inline
import random
import torch
from d2l import torch as d2l#函数功能：根据“y=Xw+b+噪声”这个线性模型生成一个人造数据集
def synthetic_data(w, b, num_examples): #X是均值为0，方差为1的大小为(num_examples, len(w))的向量X = torch.normal(0, 1, (num_examples, len(w)))#y=Xw+b+噪声y = torch.matmul(X, w) + by += torch.normal(0, 0.01, y.shape)return X, y.reshape((-1, 1))
#真实值w
true_w = torch.tensor([2, -3.4])
#真实值b
true_b = 4.2
#根据函数计算特征矩阵和标签向量
features, labels = synthetic_data(true_w, true_b, 1000)#函数功能：特征矩阵、标签向量作为输入，生成多个大小为batch_size大小的小批量batch_indices
def data_iter(batch_size, features, labels):num_examples = len(features)indices = list(range(num_examples))# 打乱样本顺序，保证随机存取random.shuffle(indices)#每次循环从i----i+batch_size的下标中获取batch_size个样本，赋值给batch_indices作为一个小批量for i in range(0, num_examples, batch_size):batch_indices = torch.tensor(indices[i: min(i + batch_size, num_examples)])#对每个小批量batch_indices计算其特征矩阵、标签向量yield features[batch_indices], labels[batch_indices]#定义初始化模型参数        
w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)  
#定义模型
def linreg(X, w, b):  """线性回归模型"""return torch.matmul(X, w) + b#定义损失函数
def squared_loss(y_hat, y): """均方损失"""return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2#定义优化算法：在每一步中，使用从数据集中随机抽取的一个小批量，然后根据参数计算损失的梯度
def sgd(params, lr, batch_size):  """小批量随机梯度下降"""with torch.no_grad():for param in params:param -= lr * param.grad / batch_sizeparam.grad.zero_()#训练过程
lr = 0.03#lr是学习率
num_epochs = 3#num_epochs是训练过程的迭代次数
net = linreg
loss = squared_loss
for epoch in range(num_epochs):for X, y in data_iter(batch_size, features, labels):l = loss(net(X, w, b), y)  # X和y的小批量损失l.sum().backward() # l中的所有元素被加到一起，并以此函数计算关于[w,b]的梯度sgd([w, b], lr, batch_size)  # 使用参数w、b的梯度更新参数w、bwith torch.no_grad():train_l = loss(net(features, w, b), labels)#输出损失值print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')