＜＜数据结构＞＞向上调整建堆和向下调整建堆的分析(特殊情况，时间复杂度分析，两种建堆方法对比，动图)

今天，我来讲讲建堆算法中使用向上调整和向下调整。

建堆的应用

在数据结构模拟堆中，我们可能会通过输入数组的元素来进行建堆或者在堆排序中，我们也需要建堆，那么建堆就有两种方法，一种从倒数第二层最右侧的父节点开始进行向下调整，直到把所有父节点都向下调整完；另外一种是从最后一个结点开始向上调整，直到每个结点都进行一次向上调整。

物理结构:实实在在在内存中是如何存储的
逻辑结构:想象出来的结构

如下面有一个数组，物理结构和逻辑结构分别如下:

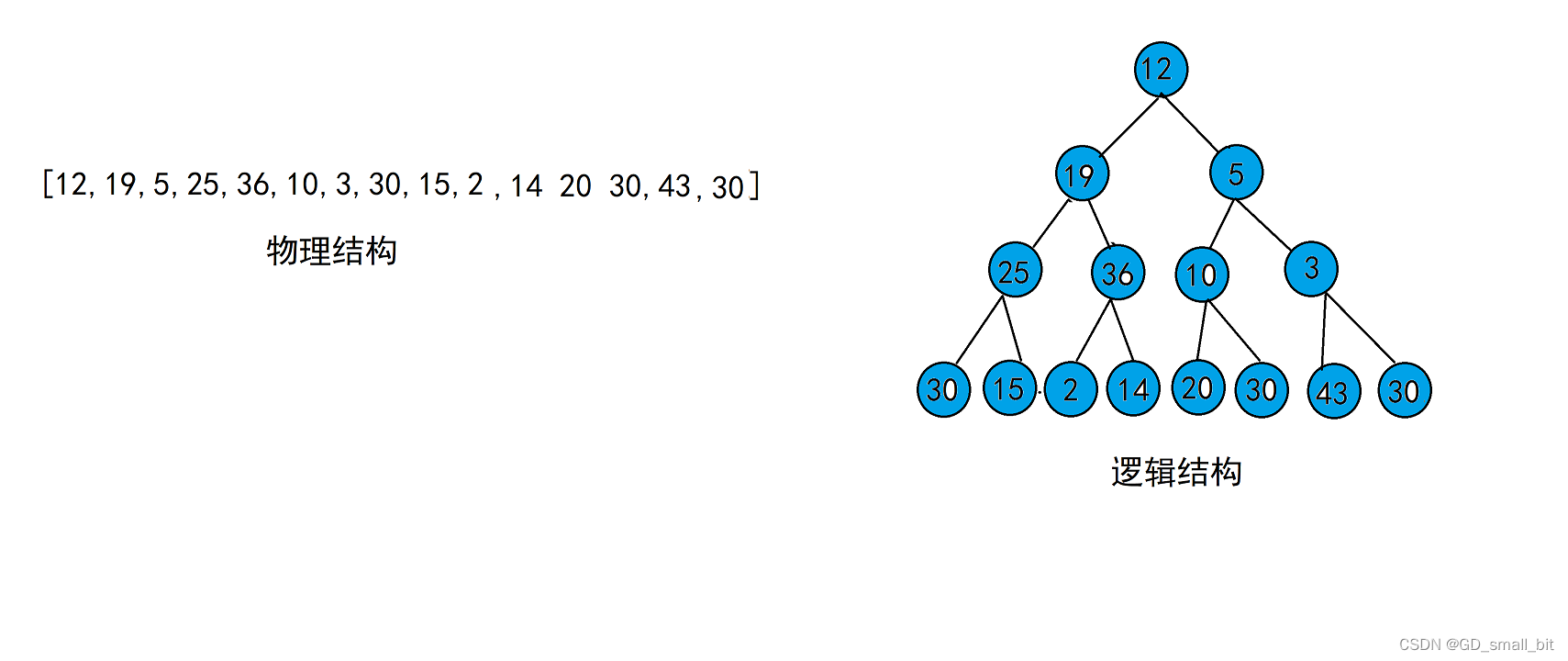
如上面数组的逻辑结构，即不满足大堆，也不满足小堆，那么我们就应该进行建堆。假设要建大堆。

接下来，我来依次进行向上调整建堆和向下调整建堆。

向上调整建堆

如上面所说，我们需要找到最后一个结点，进行向上调整，如下

这个为向上调整建堆的第一趟，接下来，将倒数第二个结点继续建堆，即43，持续下去，直到把所有的结点都进行了向上调整，那么就完成了建堆的任务。

但是这样调整真的可以吗?
下面是代码:

int swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}
Build_BigHeap(int* arr,int n)
{                                   //错误示范for (int i = n - 1; i >= 0; i--)//从最后一个结点开始，保证每个结点都能向上调整{int child = i;int parent = (child - 1) / 2;while (child > 0)              //单趟向上调整{if (arr[child] > arr[parent]){swap(&arr[child],&arr[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}}
}
int main()
{int arr[] = {12,19,5,25,36,10,3,30,15,2,14,20,30,43,30};Build_BigHeap(arr,sizeof(arr)/sizeof(arr[0]));return 0;
}

建堆前:

建堆后:

观察可以发现，在我们建堆后的逻辑结构，大部分结点都满足了大堆的要求，即父节点大于、等于孩子结点，但是有一个父结点的值小于孩子结点，是哪个呢?就是19和25，这就奇怪了，其他结点都满足大堆的要求，为什么偏偏有两个结点不满足大堆的要求呢？不着急，我要画个小动图分析一下。

由于上面的问题由第八趟向上调整导致，我就不从第一趟排序画到问题出现的地方了，因为其他的几趟的向上调整并不是影响该问题的出现的因素。但是由于前面的调整没画，此次的第八趟向上调整与从第一次向上调整画到第八趟的向上调整结果有些不同，但是并不影响，因为我们主要分析的是19和25位置的原因所在。

上面就是25出现在了19后面的原因，所以我们最开始选择最后一个元素来进行向上调整，接着依次往上找结点进行向上调整的方法存在着小bug，比如第八趟向上调整中，将25调到了最后面的一层，然后，程序就继续去向上调整数字3的位置了，却不知道25还需要与19进行调整。

那么，我应该如何改进这个bug呢，我们直接选择从第二个结点开始，也就是下标为1的位置进行向上调整，接下来，程序依次调整到最后一个结点的位置，那么就不会有问题了。

代码如下:

int swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}
Build_BigHeap(int* arr,int n)
{for (int i = 1; i <= n - 1; i++)//从第二个结点开始调整，保证每个结点都能向上调整{int child = i;int parent = (child - 1) / 2;while (child > 0)              //单趟向上调整{if (arr[child] > arr[parent]){swap(&arr[child],&arr[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}}
}
int main()
{int arr[] = { 12,19,5,25,36,10,3,30,15,2,14,20,30,43,30 };Build_BigHeap(arr, sizeof(arr) / sizeof(arr[0]));return 0;
}

建堆前

建堆后

现在，该向上调整建堆的代码就满足要求了。

向上调整建堆的时间复杂度

假设最坏的情况下，每个结点都需要向上调整

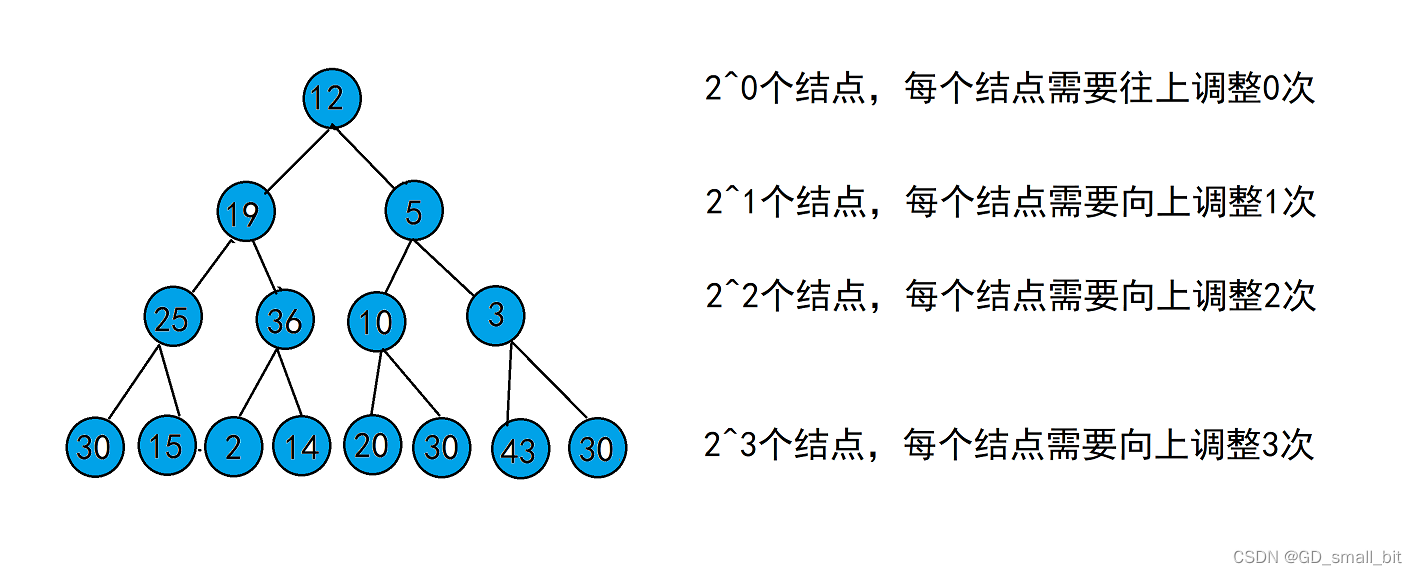
由二叉树的性质可以得知，每层结点的个数是2^(h-1)，在第几层的结点如果需要调整的话，最多需要向上调整h-1次。

那么，调整次数将与高度相关，如下

向下调整建堆

在向下调整建堆中，我们需要找到最后一个父节点，将该父节点与他的孩子结点进行比较，如果需要交换就进行交换，接下来，继续拿其他的父节点进行相同的比较，直到把所有的父节点比较完成，那么向下调整建堆就完成了。

假设我们需要建大堆，那么我们就先找到最后一个父结点，选出该父结点两个孩子结点中最大的那个结点，将该最大的孩子结点与父节点进行交换，这样就满足了大堆的要求了。

如下:第一趟向下调整的动图

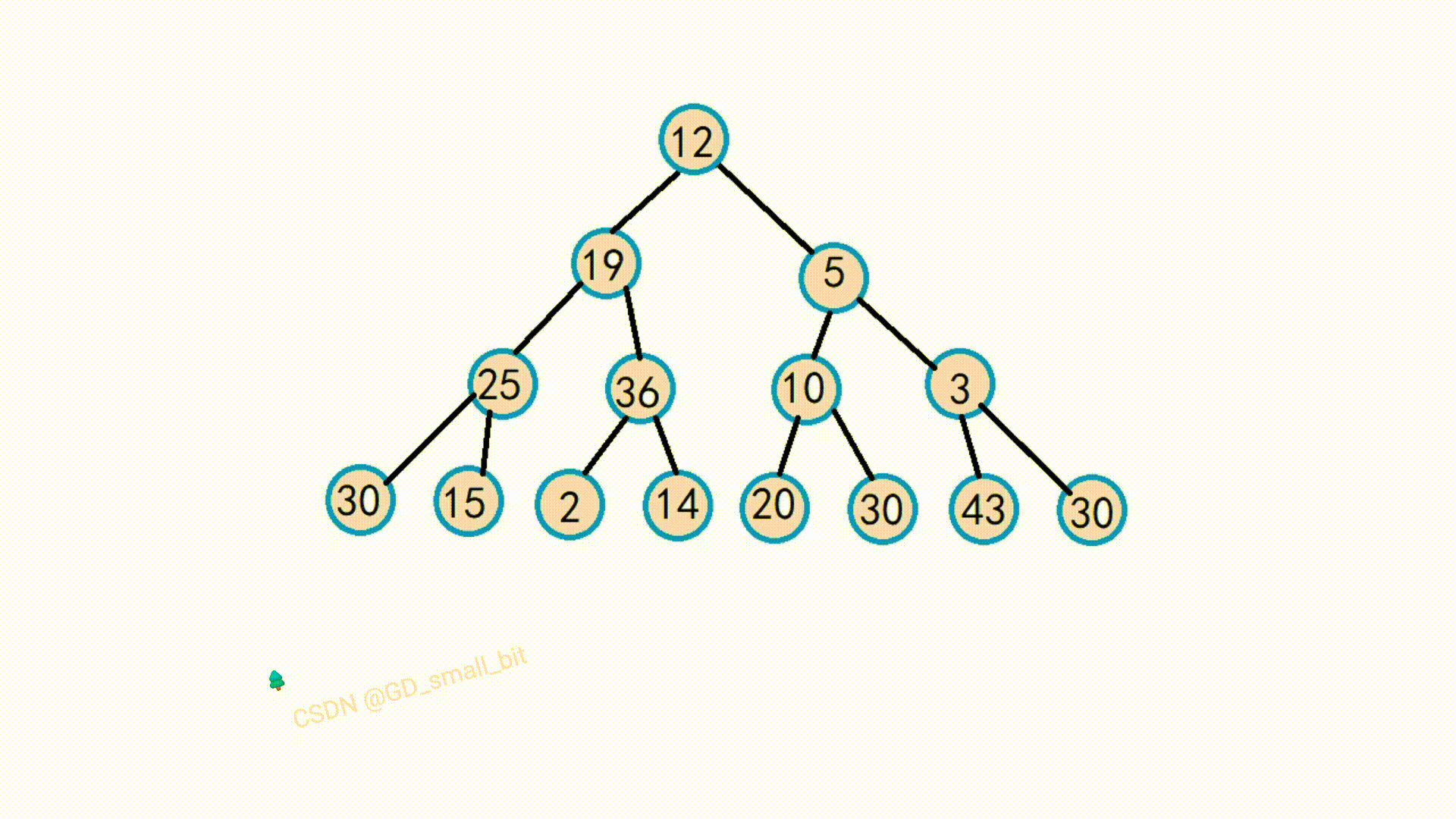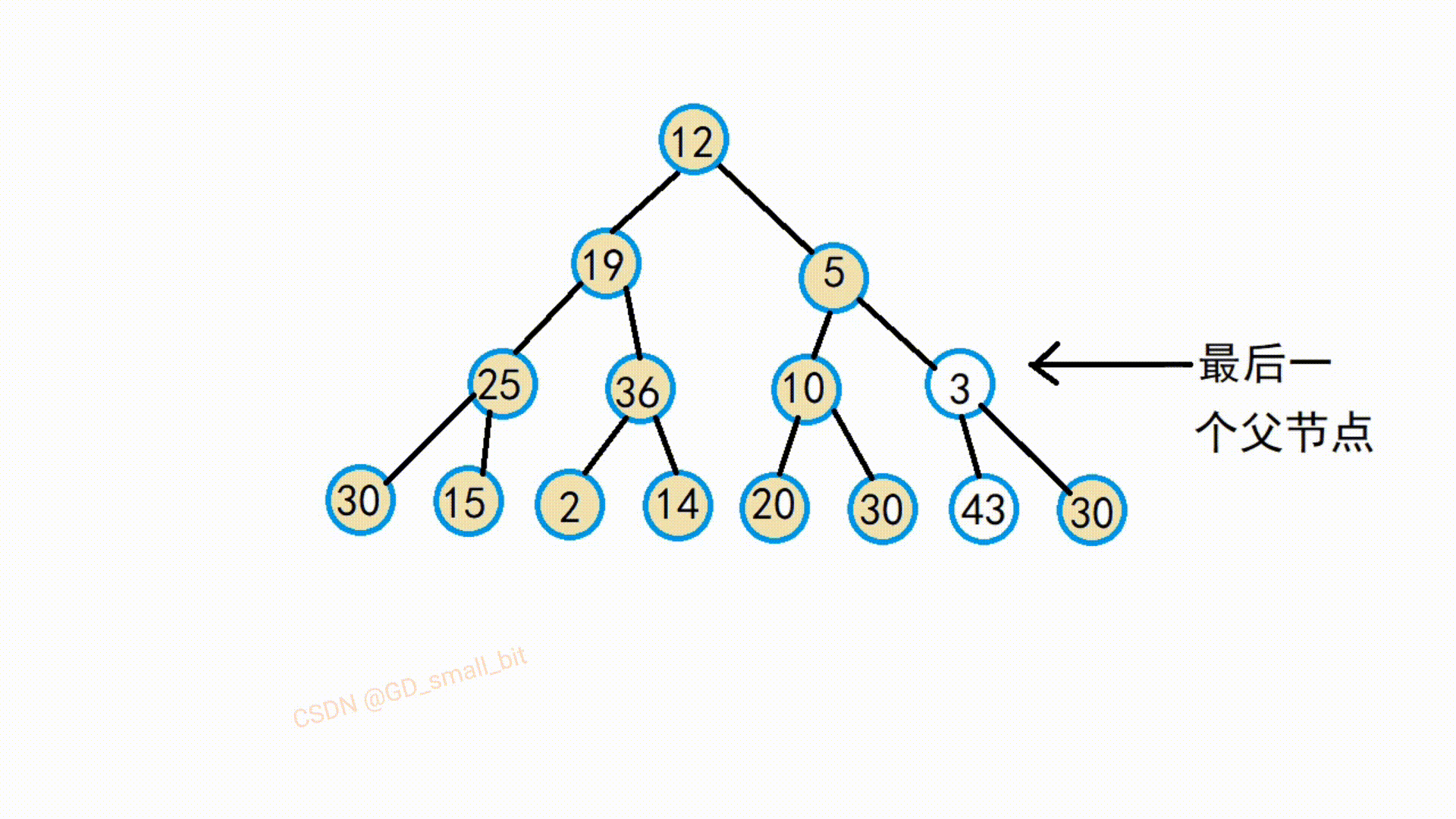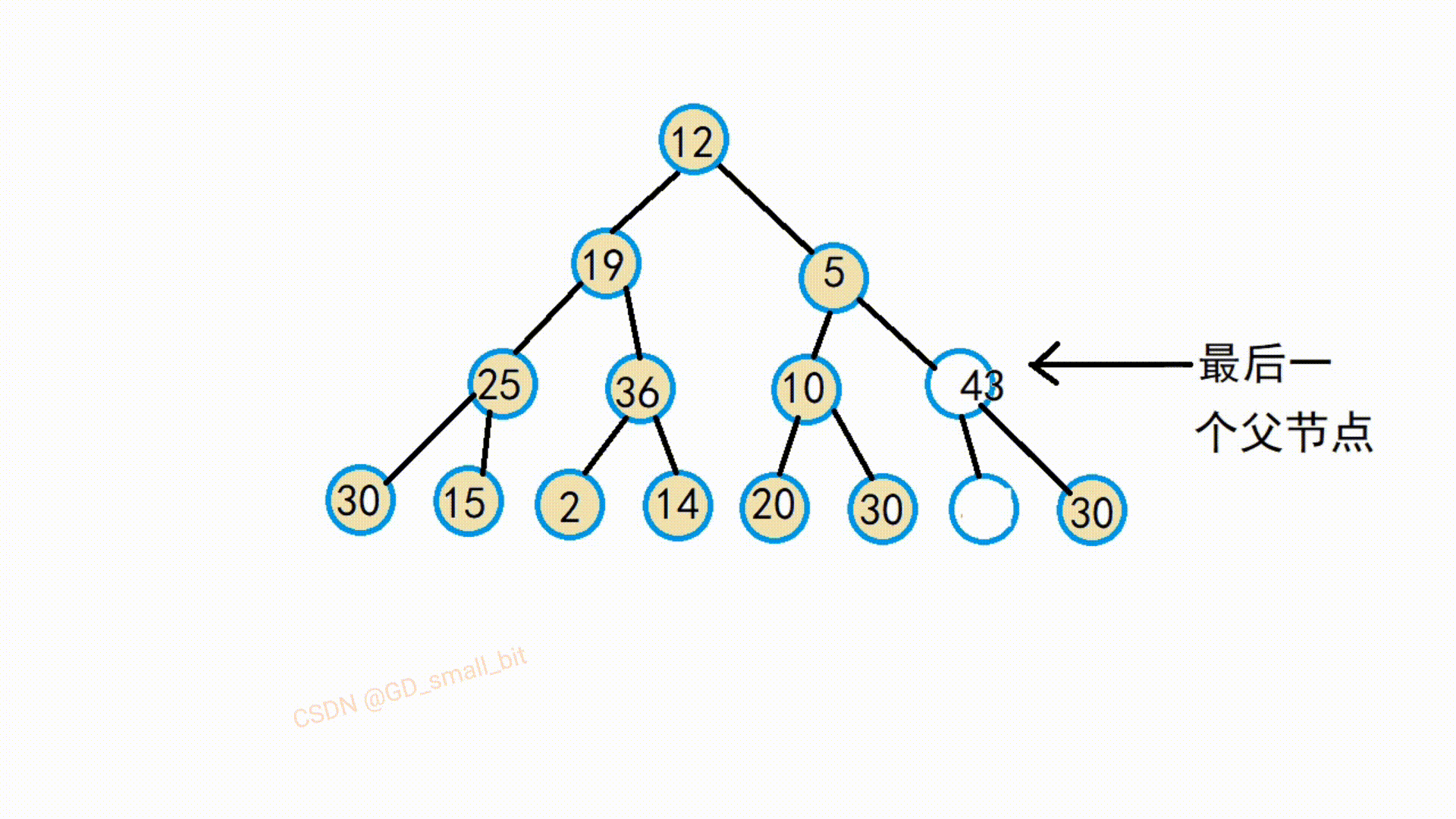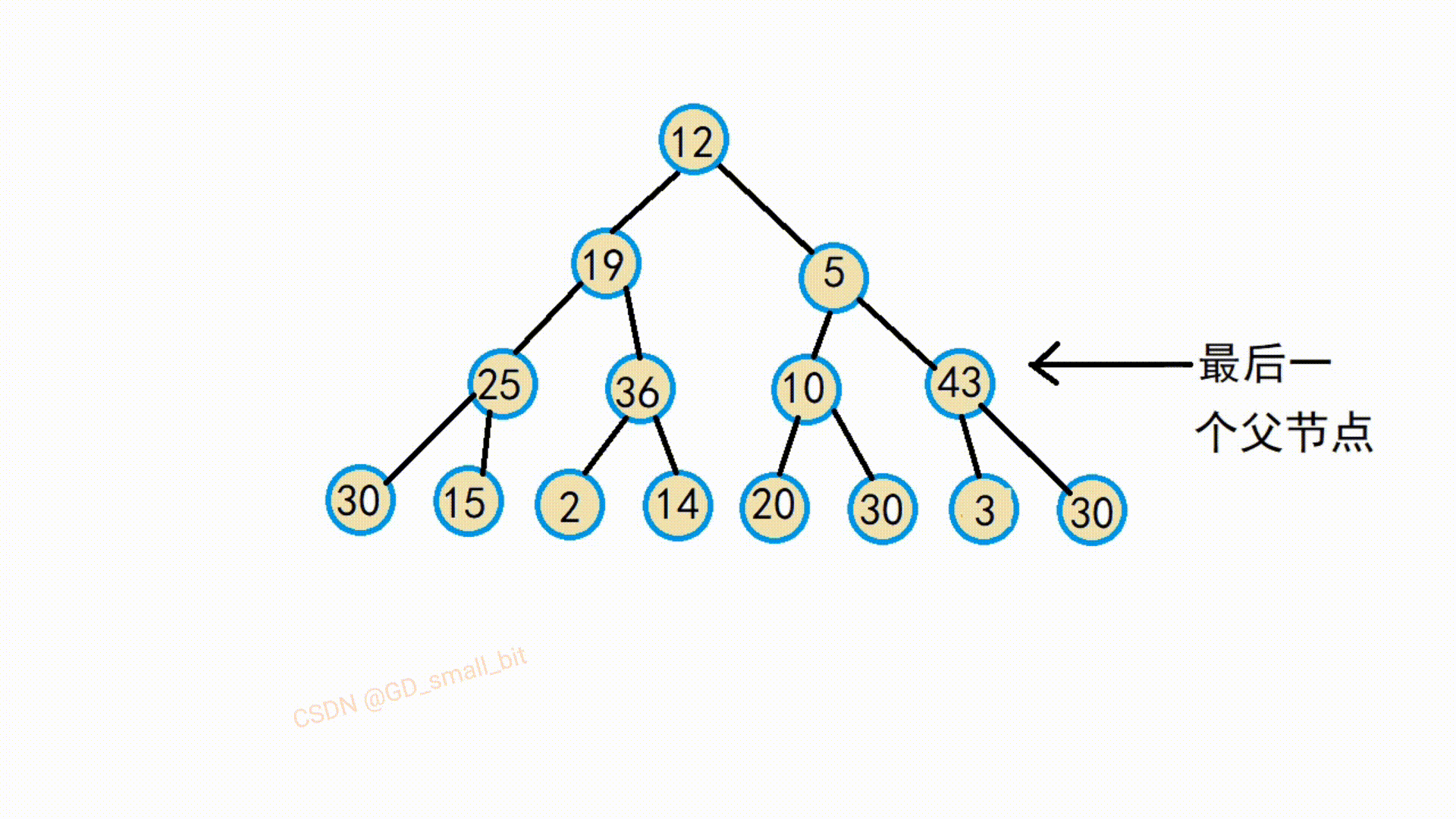
由该动图可以得知，该替换后的父节点与他的孩子结点就满足了大堆的要求了，接下来，继续往前调整，直到把所有的父节点调整完，那么整个就满足了大堆了要求了。

我再举一个调整例子吧，我并没有一步一步调整上去，而是直接调整5结点，方便大家理解代码，所以下图的10结点还没有调整。

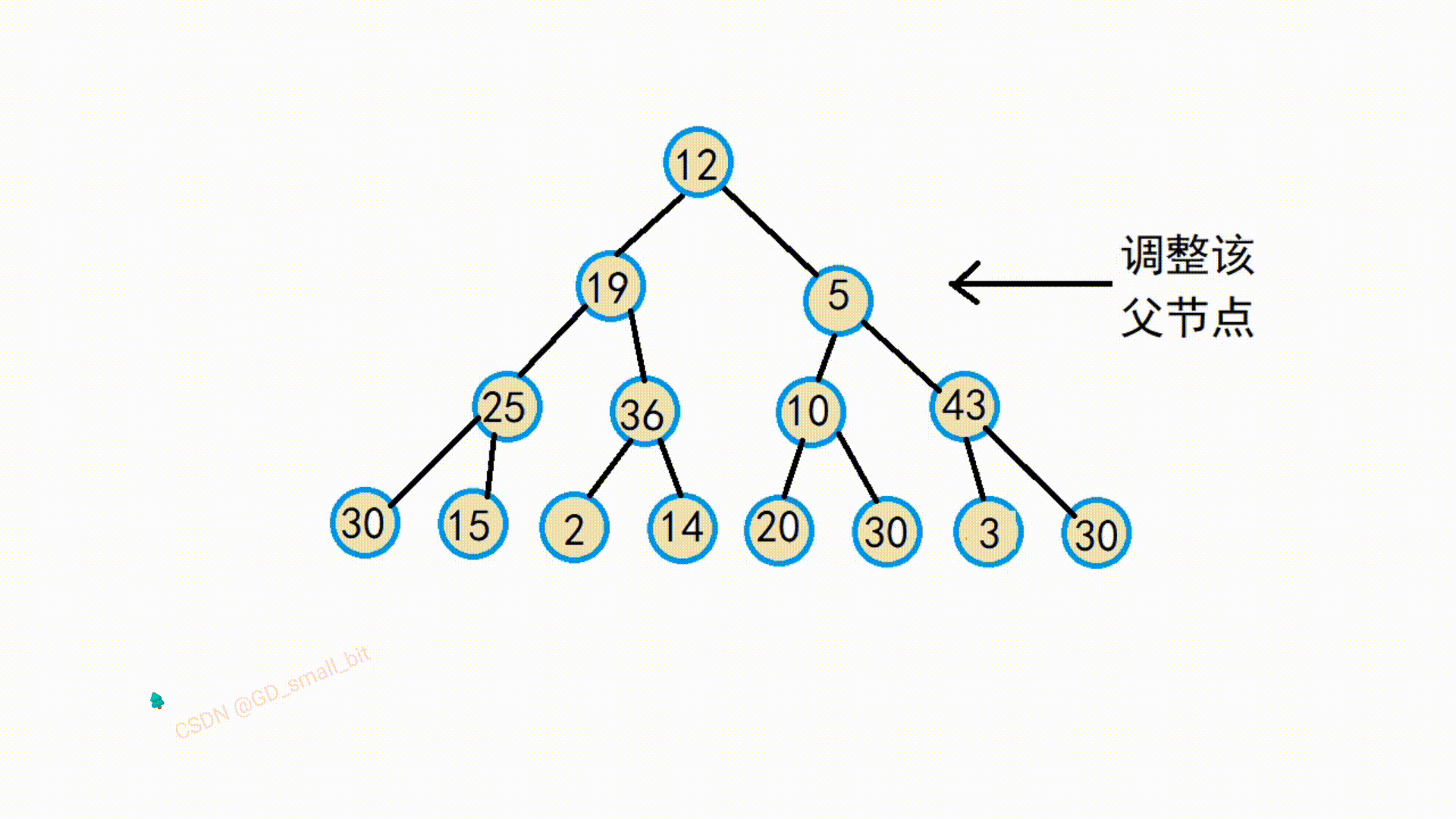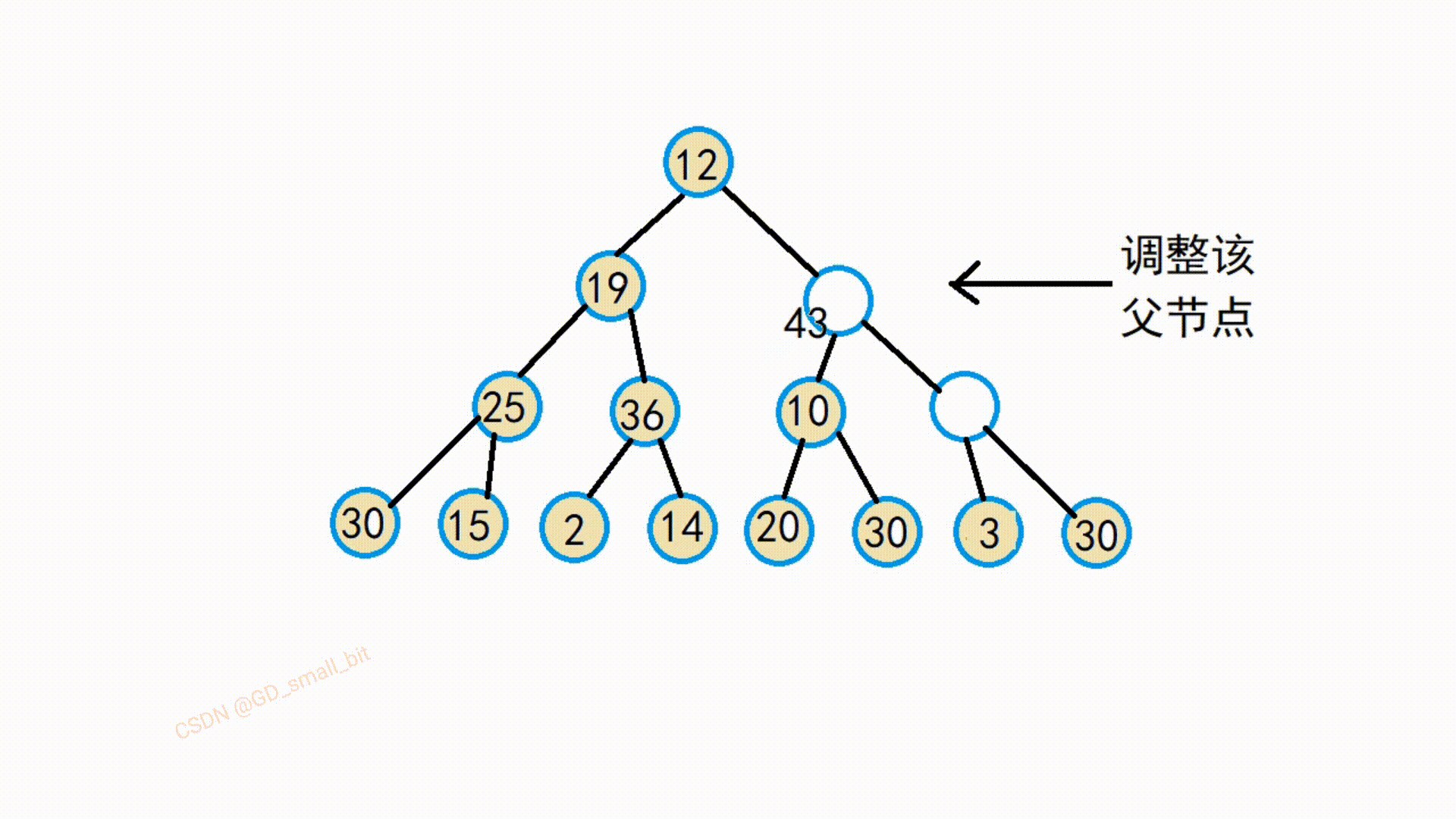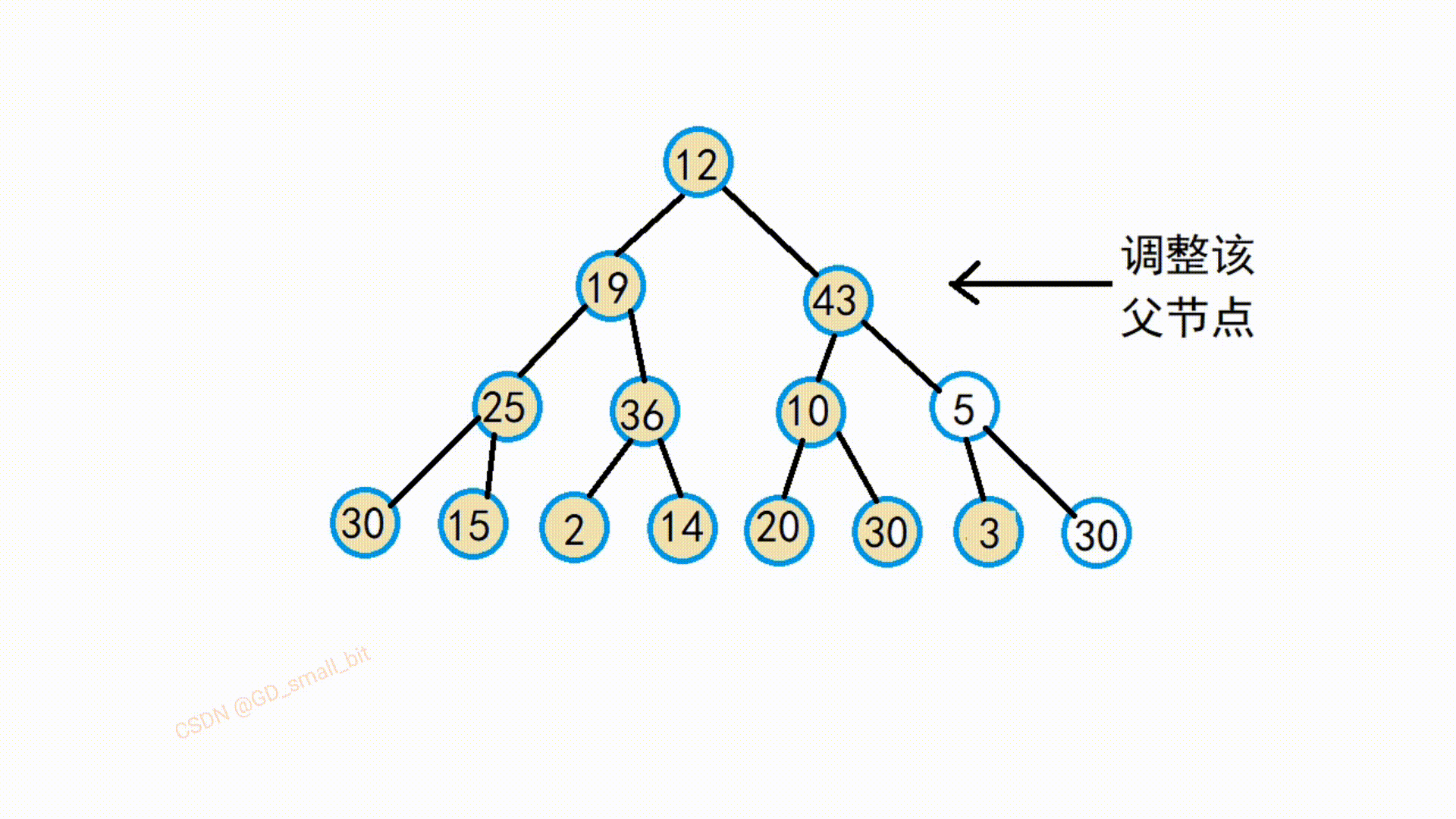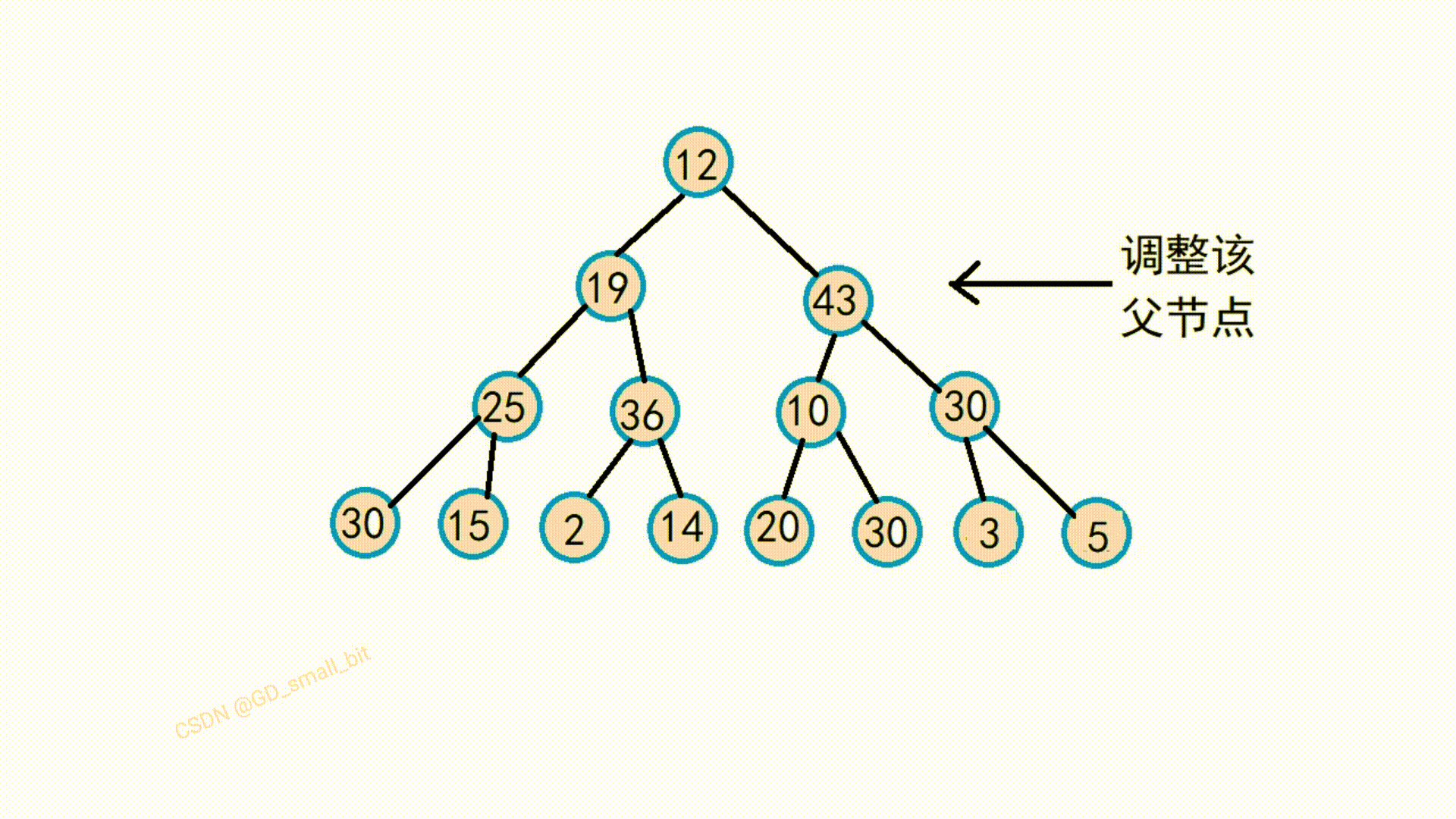
代码如下:

int swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}
Build_BigHeap(int* arr, int n)
{for (int i = (n - 1 - 1) / 2; i >= 0; i--)//从最后一个父节点结点开始调整，保证每个父结点都能向下调整{int parent = i;int child = parent * 2 + 1;while (child < n)              //单趟向下调整{if (arr[child + 1] && arr[child + 1] > arr[child]){child++;}if (arr[child] > arr[parent]){swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}
}
int main()
{int arr[] = { 12,19,5,25,36,10,3,30,15,2,14,20,30,43,30 };Build_BigHeap(arr, sizeof(arr) / sizeof(arr[0]));return 0;
}

建堆前:

建堆后:

向下调整建堆的时间复杂度

假设在最坏的情况下，所有的结点都需要向下调整。

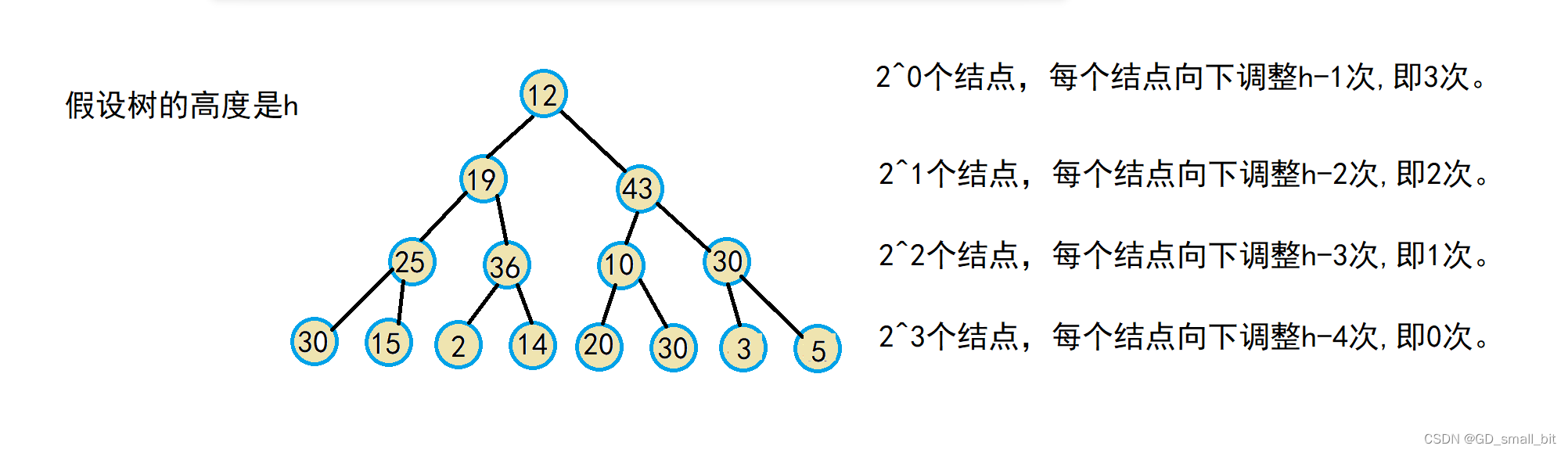
那么时间复杂度的计算如下:

向下调整建堆和向上调整建堆的选择

向上调整建堆的时间复杂度是:O(N*logN)
向下调整建堆的时间复杂度是:O(N)
所以，大多数都会选择向下调整建堆。

如果觉得写得不错，可不可以动动小手，三连支持一下。