李超树（无脑秒斜率）

一.What？

李超树个人认为用处有点大，因为会了李超树，就再也不怕斜率优化做不出来了，你但凡能够推出一个一次函数的式子那铁定用李超树。所以撒子是李超树呀？就是变异的线段树，即在某个区间内维护区间中点值最大的一条线段，然后查询就是问某个点的最大值，直接一一映射到区间中就行了。所以插入$O(\log n^2)$（常数巨小），查询$O(\log n)$。

二.How？

这里就口胡口胡。

1.插入（update）

step1：
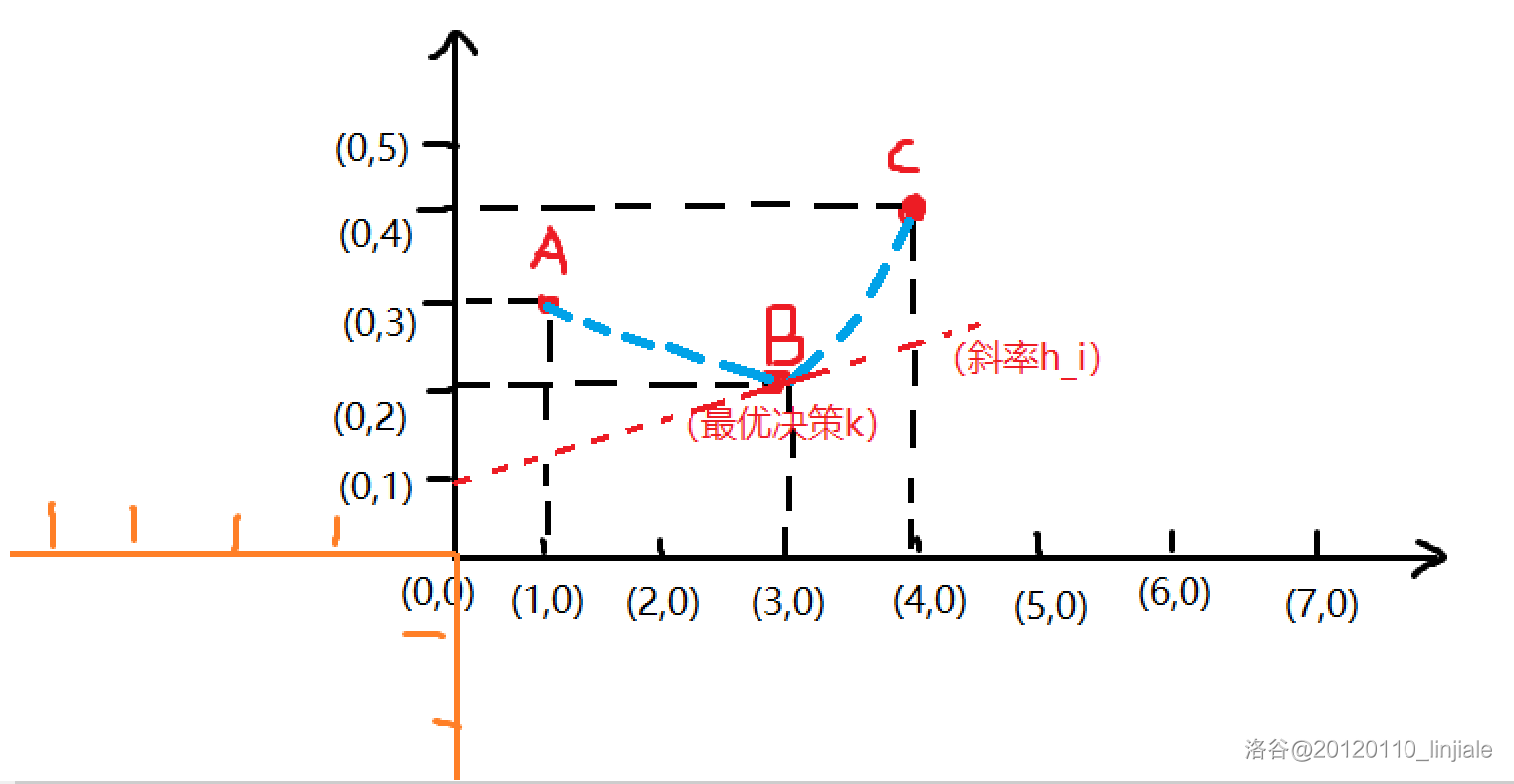
首先根据我们的定义，每个区间要保留中点值最大的一条线，所以将老线段的中点值跟新线端的中点值比较取大的一个。如果老线段的中点值要小一些就跟新线端swap一下，保证新线端中点值更小。
step2：
考虑下传，有这样两种情况：
①新线端的斜率较小：

可以看到，mid右面新线段被吊打，然而左边就不一定了，所以要更新左边。
②新线端斜率更大

可以看到，ｍｉｄ左面新线段被吊打，然而右边就不一定了，所以要更新右边。
Code：

inline void update (int Index, int l, int r, int now){int mid = l + r >> 1;if (w (now, mid) > w (t[Index], mid))swap (now, t[Index]);if (l < r){if (k[t[Index]] > k[now])update (Index * 2, l, mid, now);elseupdate (Index * 2 + 1, mid + 1, r, now);}}

2.查询（query）

显而易见，将当前区间存的线段的答案值跟子区间的答案值比较就行。

inline double query (int Index, int l, int r, int now){if (l == r){return w (t[Index], now);}int mid = l + r >> 1;if (mid >= now){return max (w (t[Index], now), query (Index * 2, l, mid, now));}else{return max (w (t[Index], now), query (Index * 2 + 1, mid + 1, r, now));}}

三.板题（ [JSOI2008]Blue Mary开公司）

#include <bits/stdc++.h>
using namespace std;#define M 50005
#define N 100005
#define LL long longint q, n;
double k[N], b[N];inline int read (){int x = 0, f = 1; char c = getchar ();while (c < '0' || c > '9') {if (c == '-') f = -1; c = getchar ();}while (c >= '0' && c <= '9') {x = x * 10 + c - 48; c = getchar ();}return f * x;
}
inline double w (int id, int pos){return k[id] * (pos - 1.0) + b[id];
}
struct Segemetree {int t[M * 4];inline void update (int Index, int l, int r, int now){int mid = l + r >> 1;if (w (now, mid) > w (t[Index], mid))swap (now, t[Index]);if (l < r){if (k[t[Index]] > k[now])update (Index * 2, l, mid, now);elseupdate (Index * 2 + 1, mid + 1, r, now);}}inline double query (int Index, int l, int r, int now){if (l == r)