【论文阅读】Interpreting and Unifying Graph Neural Networks with An Optimization Framework

【论文阅读】优化的框架来解释图神经网络（高通、低通滤波）Interpreting and Unifying Graph Neural Networks with An Optimization Framework

1. 来源

		WWW-2021,  https://doi.org/10.1145/3442381.3449953

2. 动机和贡献

图神经网络（GNNs）在图结构数据学习中受到了相当多的关注。设计良好的传播机制是GNN最基本的组成部分。虽然大多数GNN基本上遵循信息传递的方式，但人们已经努力发现和分析它们的基本关系。

• 在本文中，作者建立一个令人惊讶的连接不同传播机制与统一的优化问题，表明尽管各种网络的扩散，事实上，他们提出的传播机制是最优解优化特征拟合函数在广泛类的图内核图正则化。
• 作者提出的统一优化框架，总结了几个最具代表性的gnn之间的共性，不仅为考察不同gnn之间的关系提供了宏观的视角，也进一步为灵活设计新的gnn提供了新的机会。
• 在此框架下，现有的工作通常利用朴素的图卷积核进行特征拟合函数，并进一步开发了两个新的目标函数，分别考虑可调图核分别显示低通或高通滤波的能力。
• 此外，作者还提供了收敛性的证明和表达能力的比较。在基准数据集上的大量实验清楚地表明，所提出的gnn不仅优于现有的方法，而且具有良好的缓解过度平滑的能力，并进一步验证了用统一优化框架设计gnn的可行性。

3. 方法总览与说明

3.1 方法对比

3.2 符号说明

具有节点集 V 和边集 E 的图G =（V，E），边集V，n=|V|是节点数。这些节点是由该特征来描述的。矩阵X∈R${}^{n\times f}$，其中 f 为节点特征的维数。G的图结构可以用邻接矩阵A∈R${}^{n\times n}$来描述，其中，如果节点 i 和节点 j 之间有一条边，则为$A_{ij}$ = 1，否则为0。对角度矩阵记为 D=diag（d1，···，dn），其中$d_i={\sum }_j{A}_{ij}$。我们使用$\tilde{A}=A+I$ 来表示添加了自循环的邻接矩阵和$\tilde{D}=D+I$。然后归一化的邻接矩阵是$\hat{\tilde{A}}={\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}$。相应地，$\tilde{L}=I-\hat{\tilde{A}}$是归一化对称正半定图拉普拉斯矩阵。

4. 方法介绍

4.1 统一框架

经过设计良好的不同gnn的传播机制基本上遵循相似的传播步骤，即节点特征在一定的深度上沿着网络拓扑进行聚合和转换。在这里，作者将k层的传播机制主要总结为以下两种形式。

1. 对于具有层级特征变换的gnn（例如GCN），k层传播过程可以表示为：
   
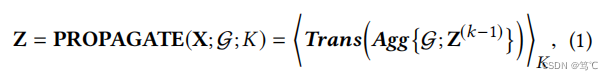
   其中$Z^0=X$和Z是K-layer传播后的输出表示。而${⟨⟩}_K$通常依赖于特定的GNN模型，表示K个卷积后的广义组合运算。 A g g { G ; Z ( k − 1 ) } Agg \{ G; Z^{(k−1)}\} Agg{G;Z(k−1)}是指沿第k次卷积运算聚合（k−1）层输出Z（k−1），Trans（·）是相应的层特征变换运算，包括非线性激活函数ReLU和层特定的可学习权重矩阵W。

2. 一些深度图神经网络（如APPNP ，DAGNN ）解耦了分层的Trans（·）和 A g g { G ; Z ( k − 1 ) } Agg \{ G; Z^{(k−1)}\} Agg{G;Z(k−1)}，并在连续的聚合步骤之前使用一个分离的特征变换：
   
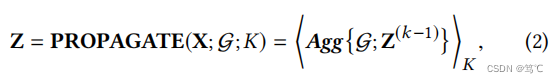
   其中$Z^{(0)}=Trans(X)$，Trans（·）可以是原始特征矩阵X上的任何线性或非线性变换运算。

此外，组合操作${⟨⟩}_K$通常是双重的：对于像GCN、SGC和APPNP这样的gnn，${⟨⟩}_K$直接利用了第K层的输出。对于使用来自其他层的输出的gnn，如JKNet和DAGNN，${⟨⟩}_K$可能表示对来自K层的一些（或全部）输出的池化、连接或注意操作。

实际上，包括聚合和转换在内的传播过程是gnn的核心。网络拓扑和节点特征是在传播过程中改进学习表示的两个最重要的信息源：网络拓扑通常对输入节点信号起低通滤波器的作用，使两个连接节点[16]的特征平滑。这样，学习到的节点表示就能够捕获图结构的同质性。对于节点特征，它本身包含复杂的信息，如低频信息和高频信息。节点特征可以灵活地用来进一步约束学习到的节点表示。例如，APPNP将原始节点特征添加到每个层学习到的表示中，这可以很好地保存个性化的信息，以减轻过度平滑。

以上分析表明，尽管不同的gnn具有不同的传播机制，但事实上，它们通常潜在的目标是实现两个目标：从特征中编码有用的信息和利用拓扑的平滑能力，这可以正式表述为以下优化目标：

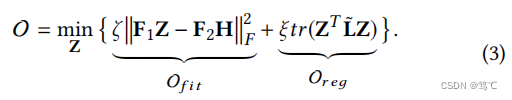
这里，ξ 是非负系数，ζ 通常从[0,1]中选择，H是对原始输入特征矩阵X的变换，F1和F2被定义为任意的图的卷积核。Z是传播后的表示，对应于最小化目标O时的最终传播结果。

在这个统一的框架中，第一部分${\mathcal{O}}_{fit}$ 是一个拟合项，通过设计不同的图卷积核f1和f2，灵活地将H中的信息灵活地编码到学习到的表示Z。图卷积核F1和F2可以从I、$\hat{\tilde{A}}$、$\tilde{L}$中选择，分别具有全通、低通、高通滤波的能力。第二项${\mathcal{O}}_{reg}$ 是一个图拉普拉斯正则化项，约束两个连接节点的学习表示变得相似，从而可以捕获同质性，${\mathcal{O}}_{fit}$ 来自于以下图拉普拉斯正则化：

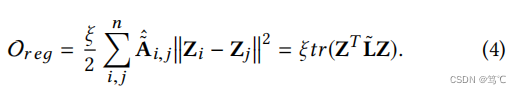
下面，作者从理论上证明了一些典型的gnn的传播机制实际上是我们提出的统一框架的特殊情况，如表1所示。这个统一的框架建立了一些典型的gnn之间的联系，能够从全面的角度来解释当前的gnn。

4.2 解释GCN和SGC

1. 图卷积网络（GCN）具有以下传播机制，可以在K层中反复进行线性变换和非线性激活：
   
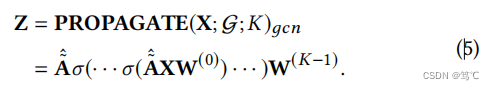
2. 简化图卷积网络（SGC）通过消除连续层之间的非线性和折叠的权重矩阵，降低了这种多余的复杂性。该线性模型表现出类似的性能，因为SGC与GCN具有相似的传播机制：
   
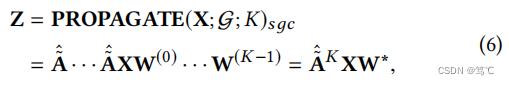
   其中，$W^{\ast }=W^{(0)}{W}^{(1)}\cdot \cdot \cdot W^{(K-1）}$。作者对所提出的统一框架下的SGC（GCN）的传播模式有以下解释:

• 定理3.1。在等式(3)中使用ζ = 0和ξ = 1，SGC/GCN的传播过程优化了以下图的正则化项：
  
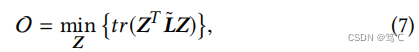
  其中，Z被初始化为XW*。
• 证明。等式的集合导数(7)相对于Z到零：
  
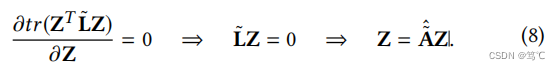
  公式(8)可以解释为 $Z_{lim}=\hat{\tilde{A}}{Z}_{lim}$ 的极限分布。然后我们使用以下迭代形式来用K→∞近似极限$Z_{lim}$：
  
  当SGC初始化输入表示为$Z^{(0)}=X{W}^{\ast }$时，等式(9)变成：
  
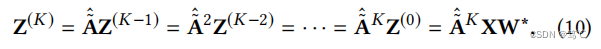
  这与SGC的传播机制相匹配。由于GCN可以通过忽略非线性变换而简化为SGC，因此这个结论也适用于GCN。

以上分析是针对连续K层图卷积运算，这里作者也关注了单层图卷积运算（GC运算），其传播机制如下：

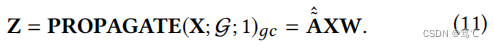
• 定理3.2。与$F_1=F_2=I$，ζ = 1，ξ = 1在等式中(3)，一层GC操作在一阶近似下优化了以下目标：
  
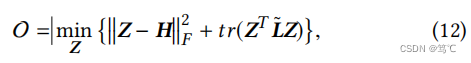
  其中，H = XW是特征上的线性变换，W是一个可训练的权值矩阵。

4.3 解释PPNP和APPNP

1. PPNP 是一种图神经网络，它利用从个性化的PageRank中衍生出来的传播机制，将特征转换从聚合过程中分离出来：
   
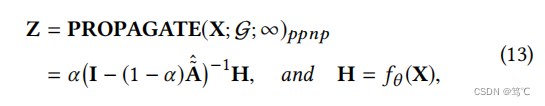
   其中，α∈(0,1]为传输概率，H为原始特征X使用MLP网络$f_{\theta }()$的非线性变换结果。
   此外，由于计算逆矩阵的复杂度高，作者采用了线性计算复杂度APPNP的幂迭代版本进行逼近。APPNP的传播过程可以看作是一个与初始变换后的特征矩阵H的残差连接的分层图卷积：
   
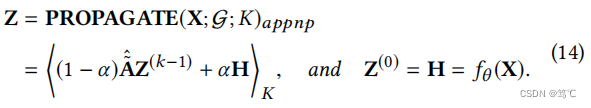
   实际上，在相关工作中已经证明了当K→∞时，APPNP收敛于PPNP，所以作者在框架下使用一个目标来解释这两者。

• 定理3.3。使用F1 = F2 = I，ζ = 1，ξ = 1/α−1，α∈(0,1] 在等式(3)，PPNP/APPNP的传播过程优化了以下目标：
  
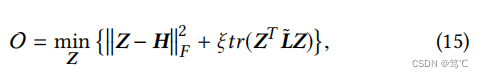
  其中，$H=f_{\theta }(X)$。
• 证明。可以设置等式的导数（15）相对于Z到零，得到最优Z为：
  
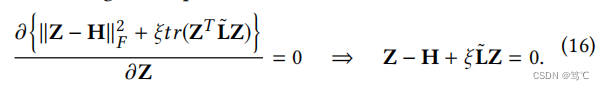
  注意，当且仅当矩阵det (M)的行列式不为零时，矩阵M就有一个逆矩阵。由于归一化拉普拉斯矩阵的特征值${\lambda }_i$∈[0,2)，而矩阵$I+\xi \tilde{L}$的特征值为（1 + ξ${\lambda }_i$）> 0。然后在等式(16)中det($I+\xi \tilde{L}$)>0和Z（16）可重写为：
  
  我们使用$\hat{\tilde{A}}$和α来重写等式 (17):
  
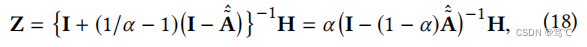
  这与PPNP的传播机制或APPNP的收敛传播结果完全一致。

4.4 解释JKNet和DAGNN

1. JKNet 是一种深度图神经网络，利用不同区域的信息。这种体系结构有选择地将来自不同层的聚合与输出处的连接/最大集中/注意相结合，即将表示法“跳转”到最后一层。

   为了方便起见，我们以类似的方式简化了第k个（k∈[1，K]）层图的卷积操作，忽略了σ(x) = x的非线性激活，并共享每个层的W* = W (0)W (1)···W（k−1）。那么第k层临时输出为$\widehat{\tilde{A^k}}XW$*。利用最后一层的注意机制，JKNet的k层传播结果可以写为：
   
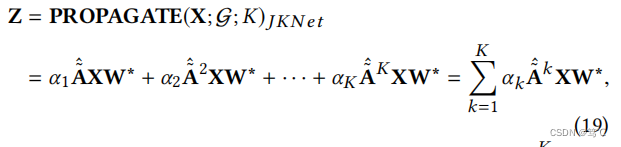
   其中α1，α2，…，αK是可学习融合权值（${\sum }_{k=1}^K{\alpha }_k=1$），为了便于分析，我们假设第k层的所有节点共享一个共同的权值αk。

• 定理3.4。使用等式中的F1 = I、F2 =$\hat{\tilde{A}}$、ζ = 1和ξ∈（0，∞）(3)，JKNet的传播过程优化了以下目标：
  
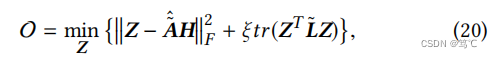
  这里的H = XW*是经过简化后的线性特征变换。

• 证明。同样地，我们可以设置等式的导数（20）相对于Z到零，得到最优Z为：
  
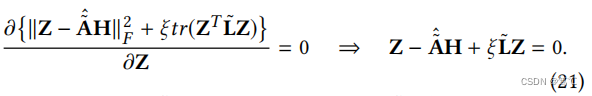
  请注意，det（I + ξ$\tilde{L}$）>0，因此矩阵{I + ξ$\tilde{L}$}${}^{-1}$存在。则相应的封闭形式的解可以写成：
  
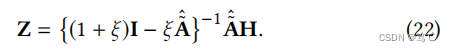
  由于∀ξ > 0的 (ξ / 1+ξ) < 1，而矩阵$\hat{\tilde{A}}$的绝对特征值以1为界，因此其所有的正幂都有有界的算子范数，那么逆矩阵可以用K→∞分解如下：
  
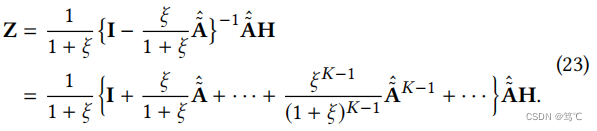
  使用H = XW*，有以下扩展：
  
  
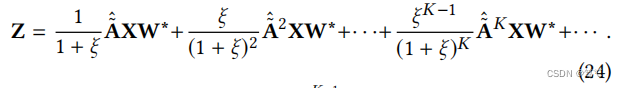
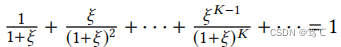
  我们可以改变coefficientξ∈（0，∞）来拟合融合权重α1，α2，···，αK.当K层足够大时，JKNet在等式中的传播机制（19）近似对应于目标的等式 (20)。

2. DAGNN 深度自适应图神经网络（DAGNN）试图自适应地整合来自大的接受域的信息。经过解耦表示转换和传播后，DAGNN的传播机制与JKNet相似：
   
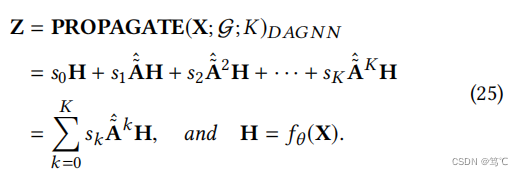
   H = $f_{\theta }(X)$是非线性特征转换MLP网络，在传播过程之前进行。$s_0,s_1,...,s_K$是可学习的保持分数（${\sum }_{k=0}^K{s}_k=1$）。我们假设所有节点的k层共享一个共同的权重sk以供方便。

• 定理3.5。在等式中使用F1 = F2 = I，ζ = 1和ξ∈（0，∞）(3)，DAGNN的传播过程优化了以下目标：
  
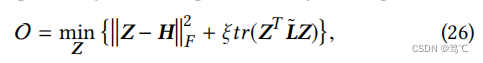
  其中，H = fθ (X)为特征矩阵上的非线性变换，保留分数s0、s1、···、sK近似为ξ∈（0，∞）。

• 证明。设置等式的导数（26）从Z到零，得到的封闭解为：
  
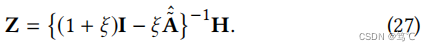
  通过类似于JKNet的分解过程，有了以下扩展：
  
  

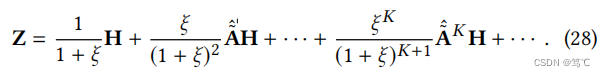
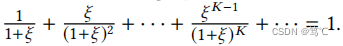
请注意，我们可以更改ξ∈（0，∞）以适应保留分数。然后，DAGNN的传播机制近似对应于目标等式 (26)。

4.5 讨论

为了清晰起见，作者总结了表1中不同gnn与相应的目标函数之间的总体关系。可以看出，作者提出的框架抽象了代表性gnn之间的共性。基于这个框架，可以更容易地理解他们之间的关系。例如，定理3.1中SGC对应的优化目标只有一个图正则化项，而定理3.3中APPNP对应的优化目标同时具有拟合项和图正则化项。目标函数的显式差异很好地解释了deep APPNP（PPNP）在过平滑问题上优于SGC（GCN），因为另外需要学习到的表示对原始特征进行编码。

另一方面，作者提出的框架通过对目标优化函数进行数学建模，显示了gnn的一个大图景。考虑到不同的现有gnn可以适应这个框架，gnn的gnn变体也可以很容易地出现。我们所需要的就是在这个框架内根据特定的场景设计不同的变量（例如，不同的图卷积内核F1和F2），可以很容易地推导出相应的传播，并且可以自然地设计新的gnn架构。新设计的模型具有一个目标目标函数，更易于解释，更可靠。

5. GNN-LF/HF：作者提出的模型

基于统一的框架，作者发现当前大多数gnn简单地在特征拟合项中将F1和F2设为I，这意味着它们需要将H中的所有原始信息编码到z中。然而，事实上，H可能不可避免地包含噪声或不确定信息。注意到JKNet传播目标，利用F2=$\hat{\tilde{A}}$，可以编码低频信息在H到Z中。在现实中，情况更复杂，因为很难确定什么信息应该编码，只考虑一种类型的信息不能满足不同下游任务的需要，有时高频或所有信息甚至是有用的。在本节中，我们将重点设计新的f1和f2，以便在该框架下灵活地编码更全面的信息。

5.1 带有低通滤波内核的GNN

5.1.1 目标函数

作者首先考虑在原始和低通滤波空间中建立H和Z的关系。

• 定理4.1。 F 1 = F 2 = { µ I + （ 1 − µ） A ~ ^ } 1 / 2 ，µ ∈ [ 1 / 2 , 1 ) F1=F 2=\{µI+（1−µ）\hat{\tilde{A}}\}^{1/2}，µ∈[1/2,1) F1=F2={µI+（1−µ）A~^}1/2，µ∈[1/2,1)，ζ = 1和ξ = 1/α−1，α∈（0, 2/3）(3)，灵活低通滤波核的传播过程为：
  
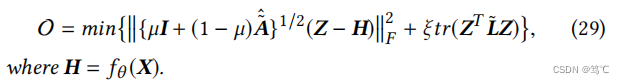
  注意，µ是一个平衡系数，作者设置了µ∈[1/2,1)，使 $\mu I+(1-\mu )\hat{\tilde{A}}=V\Lambda V^T$是一个对称的正半定矩阵。因此，矩阵 { µ I + ( 1 − µ ) A ~ ^ } 1 / 2 = V Λ 1 / 2 V T \{µI+(1−µ)\hat{\tilde{A}}\}^{1/2}=VΛ^{1/2}V ^T {µI+(1−µ)A~^}1/2=VΛ1/2VT在谱域上具有类似于$\mu I+(1-\mu )\hat{\tilde{A}}$ 的滤波行为。并且我们设置了α∈（0,2/3），以确保第4.1.3小节中的迭代近似解具有正系数。通过调整平衡系数µ，所设计的目标可以灵活地约束Z和H在原始和低通滤波空间中的相似性，有利于满足不同任务的需要。

5.1.2 封闭解方法

为了最小化等式中的目标函数（29），作者设置了等式的导数（29）从Z到零，推导出相应的封闭解如下：

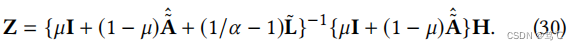
可以重写等式（30）使用$\hat{\tilde{A}}$作为：

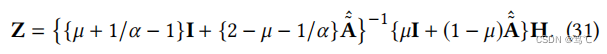
5.1.3 迭代近似法

考虑到矩阵反演导致的封闭解的计算效率低下，我们可以使用以下迭代逼近解，而不构造稠密逆矩阵：

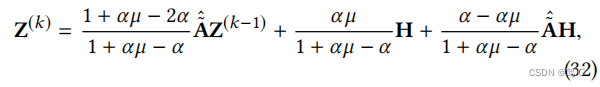
它在等式中收敛于封闭形式的解（31）当k→∞和使用α∈（0,2/3）时，所有的系数都总是正的。

5.1.4 模型设计

利用推导的两种传播策略（31）和等式（32），我们提出了两种新的封闭形式和迭代形式的gnn。请注意，作者将所提出的模型表示为带有低通滤波图卷积核（GNN-LF）的GNN。

• 闭合式GNN-LF。利用等式中的封闭形式的传播矩阵（31），我们用µ∈[1/2,1)、α∈（0,2/3）和H = fθ (X)定义了以下传播机制：
  
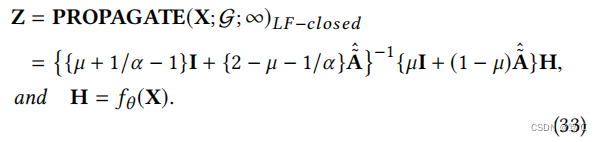
  这里我们首先得到一个非线性变换结果H特性与MLP网络X fθ（·），并使用设计传播矩阵 { { µ + 1 / α − 1 } I + { 2 − µ − 1 / α } A ~ ^ } − 1 \{\{µ+ 1/α−1\}I+ \{2−µ−1/α\}\hat{\tilde{A}}\}^{−1} {{µ+1/α−1}I+{2−µ−1/α}A~^}−1 传播H和AH，然后我们可以得到表示编码特性信息从原始和低频空间。

• 迭代式GNN-LF。利用等式中的形式传播机制（32），我们可以用µ∈[1/2,1)，α∈（0,2/3）设计一个深度和计算效率高的图神经网络：
  
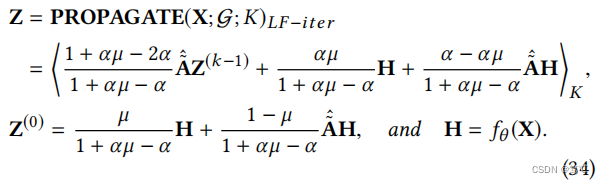
  作者直接使用k层输出作为传播结果。这种迭代传播机制可以看作是基于分层$\hat{\tilde{A}}$的邻域聚合，在特征矩阵H和滤波后的特征矩阵$\hat{\tilde{A}}$H上有残差连接。请注意，解耦了层级转换和聚合过程，这有助于缓解过度平滑问题。

GNN-LF迭代和GNN-LF闭合有以下关系：

• 定理4.2。在K→∞下，深GNN-LF-迭代收敛到GNN-LF-闭合，传播结果与等式相同 (31)。
• 证明。使用GNN-LF-迭代进行k层传播后，相应的输出结果Z可以写为：
  

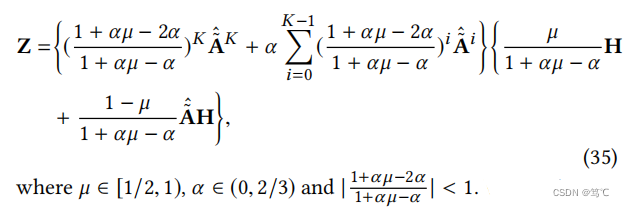
当K→∞时，左项趋于0，右项变成几何级数。该级数收敛，因为$\hat{\tilde{A}}$的绝对特征值界为1，然后是等式（35）可重写为：

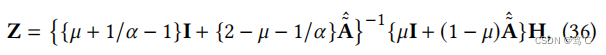
这正好是计算GNN-LF-闭的方程。

GNN-LF的训练也与其他gnn相同。例如，它评估了半监督多类节点分类任务中所有标记示例的交叉熵损失。

5.2 带有高通滤波内核的GNN

5.2.1 目标函数

与GNN-LF类似，现在考虑在原始和高通滤波空间中保持H和Z的相似性。为了便于后续的分析，我们选择了以下目标：

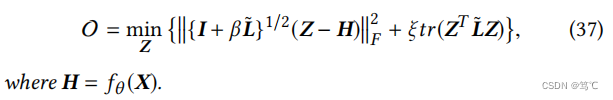
类似地，β也是一个平衡系数，设置β∈（0，∞），使$I+\beta \tilde{L}=V^{\ast }{\Lambda }^{\ast }{V^{\ast }}^T$也是一个对称的正半定矩阵，而矩阵 { I + β L ~ } 1 / 2 = V ∗ Λ ∗ 1 / 2 V ∗ T \{I + β\tilde{L}\}^{1/2}=V^*{Λ^*}^{1/2}{V^∗}^T {I+βL~}1/2=V∗Λ∗1/2V∗T具有类似于$I+\beta \tilde{L}$的过滤行为。在等式中可以看到（37），通过调整平衡系数β，设计的目标可以灵活地约束Z和H在原始空间和高频空间中的相似性。

5.2.2 封闭解方法

计算出的封闭形式的解为：

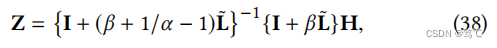
它也可以重写为：

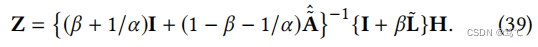
5.2.3 迭代近似法

考虑到逆矩阵的计算效率低下，作者在不构造密集逆矩阵的情况下给出了以下迭代近似解：

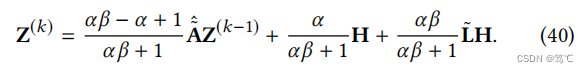
5.2.4 模型设计

利用推导的两种传播策略（39）和在等式中（40），我们提出了两种新的封闭形式和迭代形式的gnn。类似地，我们使用GNN-HF来用高通滤波图卷积核表示GNN。

• GNN-HF-闭合式。利用等式中的封闭形式的传播矩阵（39），我们定义了以下具有封闭传播机制的新型图神经网络：
  
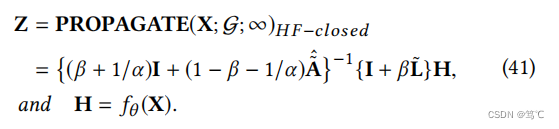
  注意，β∈（0，∞）和α∈(0,1]。通过将传播矩阵$\{(\beta +1/\alpha )I+(1-\beta -1/\alpha )\hat{\tilde{A}}{\}}^{-1}$直接应用于H和$\tilde{L}$H矩阵上，可以从原始空间和高频空间中得到表示编码特征信息。

• GNN-HF-迭代式。利用迭代传播机制，我们有了一个具有β∈（0，∞）和α∈(0,1]的深度和计算效率高的图神经网络。
  
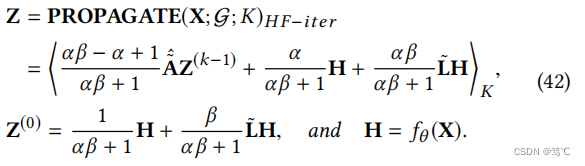
  我们直接使用k层输出作为传播结果。同样，这种迭代传播机制可以看作是基于分层$\hat{\tilde{A}}$的邻域聚合，以及特征矩阵H和高频滤波特征矩阵$\tilde{L}$H上的残差连接。并解耦了传播过程中的分层转换和聚合过程。

GNN-HF迭代式和GNN-HF闭合式有以下关系：

• 定理4.4。当K→∞时，深GNN-HF-iter收敛于GNN-hf闭合，其传播结果与等式相同 (39)。

6. 频谱表达能力分析

在本节中，我们研究了图谱域中的几种传播机制，以检验它们的表达能力。将具有f个输入信道的图信号$X\in R^{n\times f}$上的K阶多项式滤波器定义为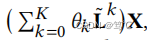：其中，θk为对应的多项式系数。作者假设图信号X是非负的，X可以通过线性变换转换为输入信号H。我们的目的是比较不同gnn的多项式系数θk，并表明具有K阶灵活多项式滤波器系数的GNN-LF/HF具有更好的光谱表达能力。为了简洁，作者主要分析了GNN-LF的滤波器系数，而SGC、PPNP、GNN-HF的光谱分析见附录。

6.1 滤波器系数分析

6.1.1 GNN-LF的分析

从定理4.2的分析中，我们得到了GNN-LF-iter在等式中的扩展传播结果（35），已证明收敛于传播结果gnn-lf-用K→∞关闭。将此传播结果进行分析，当K→∞时，我们有以下过滤表达式：

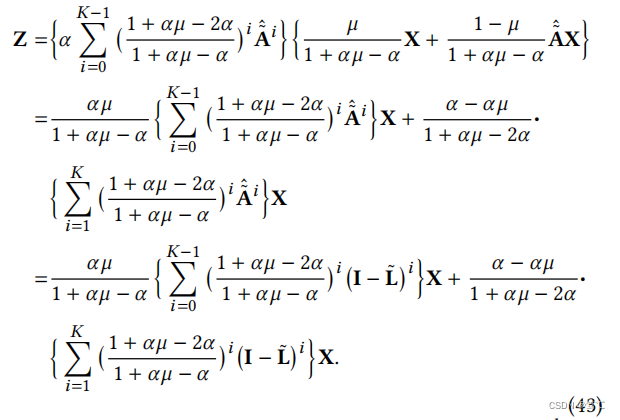
如果展开上述方程，则${\tilde{L}}^k$（k∈[0，K]）上的滤波器系数可以归纳为以下形式：

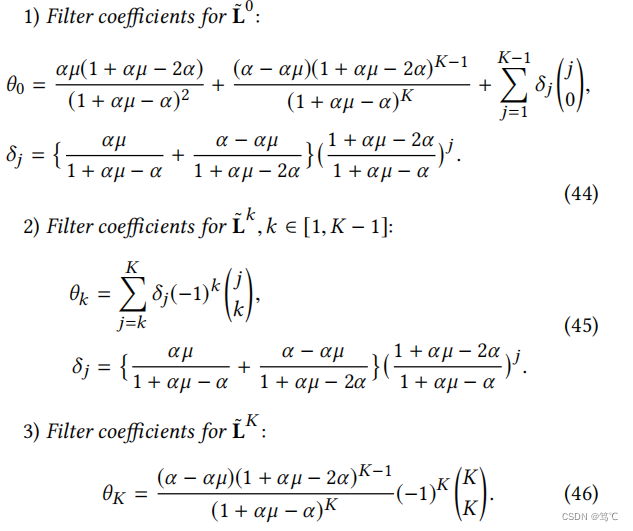
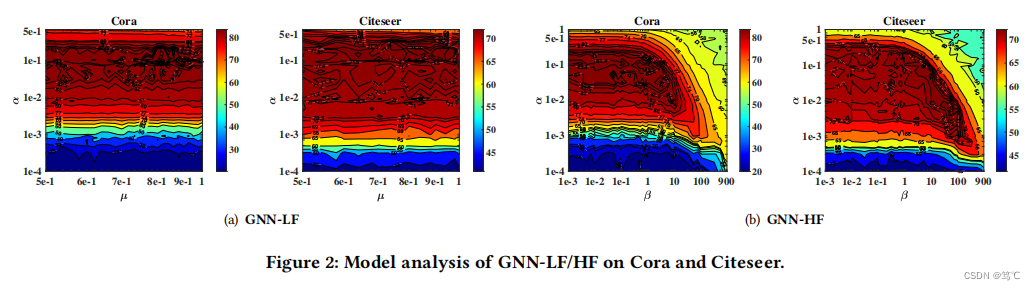
从上述对GNN-LF的分析结果中，我们发现滤波器系数的表达形式依赖于不同的k，并由两个可调因子α和µ决定，这提高了光谱滤波器的表达能力，进一步缓解了过平滑问题。

6.1.2 SGC/PPNP/GNN-HF的分析

GNN-HF的分析与GNN-LF的分析相似，为了简洁，作者在附录中分析了它们。

6.2 表达能力的分析

正如相关论文所指出的，过度平滑问题的原因是典型的GCN收敛于随机游动的极限分布，与输入特征隔离，使节点随着层数的增加而表示不可分割。[4]还从多项式滤波器系数的角度给出了另一个理解，并指出灵活的和任意的滤波器系数对于防止过度平滑是必要的。

我们可以发现： 1) SGC或k层图卷积运算具有固定的常数滤波系数，这限制了表达能力，进一步导致过度平滑。2) PPNP对SGC（GCN）具有更好的滤波表达能力，因为k阶的滤波系数随因子α一起是可变化的。3)与PPNP和SGC（GCN）相比，GNN-LF/HF在可调因子α、µ或β的影响下更具表现力，提高了多项式滤波器任意系数的拟合能力，有助于GNN-LF/HF缓解过平滑问题。从PPNP [14]、GNN-LF在等式中的极限分布来看（36），等式中的GNN-HF（53），我们还可以发现，它们都收敛于一个同时包含输入特征和网络结构信息的分布。这一特性还有助于减少过度平滑对PPNP/GNN-LF/GNN-HF的影响，即使层数趋近于无穷大。

7. 实验

7.1 数据集

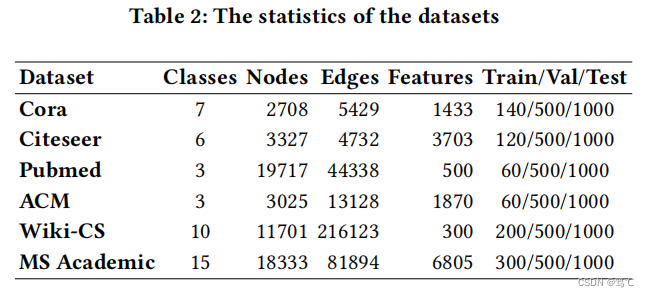
7.2 实验结果

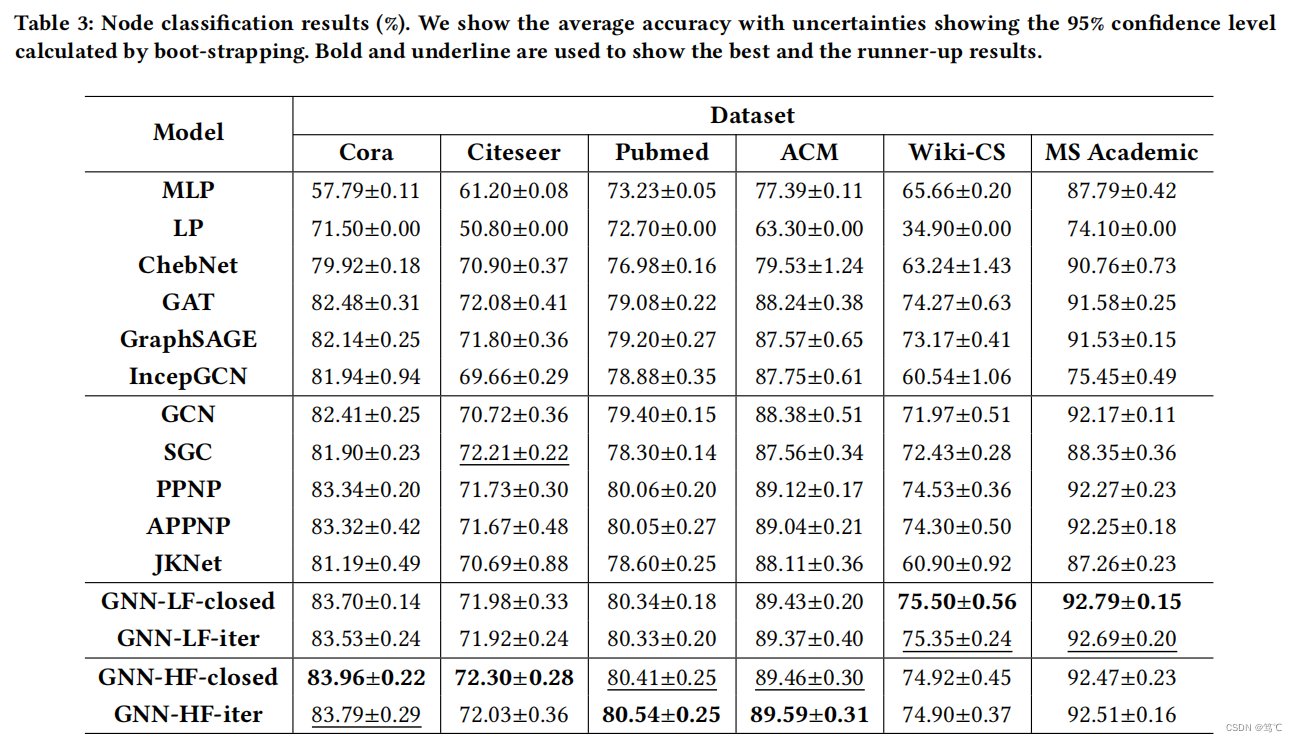
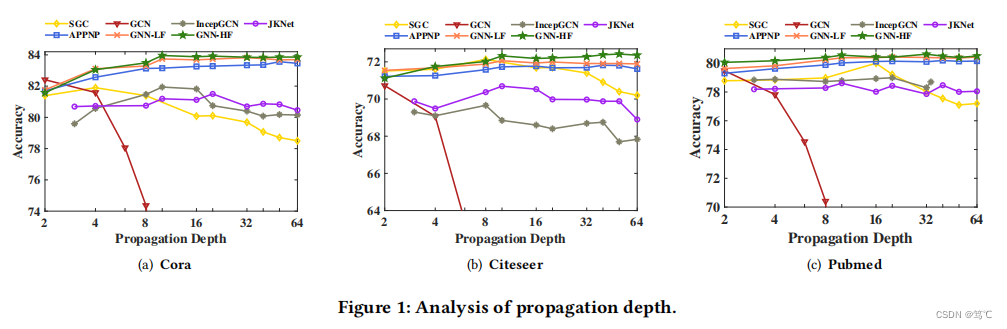
8. 总结

本文研究了不同gnn传播机制的内在关系。作者建立了不同的gnn之间的联系和一个灵活的目标优化框架。所提出的统一框架提供了一个理解和分析不同gnn的全局视角，这进一步使我们能够识别当前gnn的弱点。在此基础上，提出了两种具有可调卷积核的具有低通和高通滤波能力的新型gnn，并分析了其优异的表达能力。大量的实验很好地证明了这两种gnn在真实世界数据集上优于最先进的模型。