本文主要是介绍『最小生成树』Prim算法——加点法(优先队列/堆优化 + C++实现 + 例题),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
『算法原理』
在一个连通网的所有生成树中,各边的代价之和最小的那颗生成树称为该连通网的最小代价生成树(Minimum Cost Spanning Tree),简称最小生成树(MST)。
Prim算法之所以叫加点法,就是因为其本质是一个点一个点地加入到最小生成树中。
算法步骤如下:
设有一无向连通图G,有n个顶点。
- a.初始化——任意找图中的一点作为源点,视为最开始的生成树,然后更新所有的点和生成树的权值(距离),将不能直接和生成树连通的点的权值赋为无穷大。
- b.加点——将离生成树最近的(权值最小)的点V加入到生成树中,然后更新生成树和其他生成树外的点的距离(权值)
- c.重复b步骤直至所有顶点都被加入到生成树中,即生成树中加入了n个点
下面用图示来解释这个过程。
对于图G
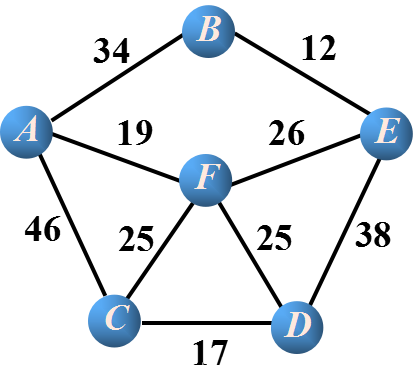
a.初始化——任意找图中的一点作为源点,视为最开始的生成树,然后更新所有的点和生成树的权值(距离),将不能直接和生成树连通的点的权值赋为无穷大。(这里选取 A 作为源点)
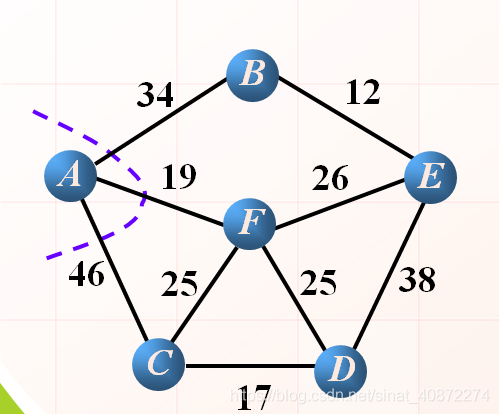
- U={A}
- V-U={B, C, D, E, F}
- cost={(A, B)34, (A, C)46, (A, D
这篇关于『最小生成树』Prim算法——加点法(优先队列/堆优化 + C++实现 + 例题)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



