本文主要是介绍AUC 随机抽取一个阳性样本和一个阴性样本,分类器正确判断阳性样本的值高于阴性样本之机率,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
随机抽取一个阳性样本和一个阴性样本,分类器正确判断阳性样本的值高于阴性样本之机率=AUC
随机取两个样本,正样本排在负样本之前的概率
为什么要用AUC
-
因为ROC曲线有个很好的特性:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。
-
在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),此时如果用precision/recall等指标的话,数据分布的波动就会出现预测的较大波动
-
AUC考虑了分类器对于正例和负例的分类能力,在样本不平衡的情况下,依然能够对分类器作出合理的评价
-
下图是ROC曲线和Precision-Recall曲线的对比,(a)和(c)为ROC曲线,(b)和(d)为Precision-Recall曲线。(a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结果,(c)和(d)是将测试集中负样本的数量增加到原来的10倍后,分类器的结果。
-
可以看出,ROC曲线基本保持原貌,而Precision-Recall曲线则变化较大。
平面的横坐标是false positive rate(FPR),纵坐标是true positive rate(TPR)
- ROC曲线是一系列threshold下的(FPR,TPR)数值点的连线。此时的threshold的取值分别为测试数据集中各样本的预测概率,但取各个概率的顺序是从大到小的。
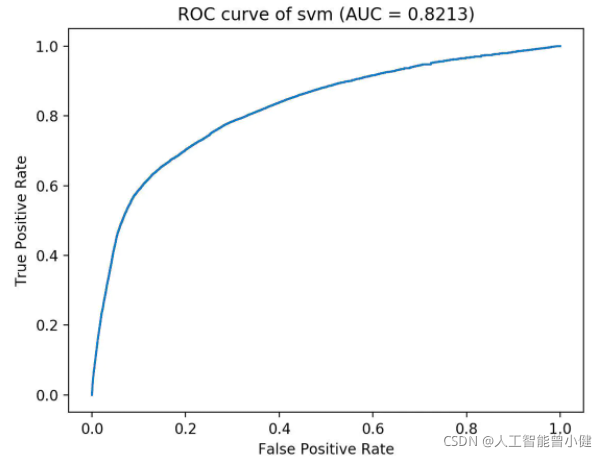
AUC
AUC其实就是上面ROC曲线下的面积,最多的就是说AUC评估的是随机给定一个正样本和一个负样本,模型对正样本的预测概率大于模型对于负样本预测概率的概率,听起来很绕口,但是呢,你别说,AUC还真是表达的是这么个含义。
啰嗦了这么多,本文的重点来了,既然我说了AUC就是表达的这么个含义,那么我肯定得给出数学证明,因为涉及到许多的公式,所以我这里选择以贴图的形式来推导,使用的设备还是我的小ipad(这东西真香),下面开始整。
证明
我这里全部使用我用ipad画的图了~有点难看,大家凑合看一下吧,讲的不明白的地方可以留言。
按照定义,AUC即ROC曲线下的面积,而ROC曲线的横轴是FPRate,纵轴是TPRate,当二者相等时,即y=x,如下图: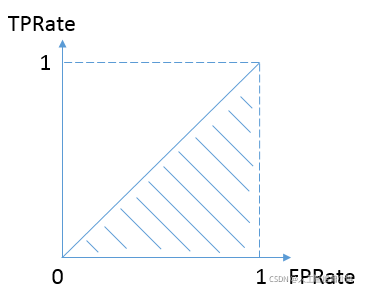
表示的意义是:对于不论真实类别是1还是0的样本,分类器预测为1的概率是相等的。
换句话说,分类器对于正例和负例毫无区分能力,和抛硬币没什么区别,一个抛硬币的分类器是我们能想象的最差的情况,因此一般来说我们认为AUC的最小值为0.5(当然也存在预测相反这种极端的情况,AUC小于0.5,这种情况相当于分类器总是把对的说成错的,错的认为是对的,那么只要把预测类别取反,便得到了一个AUC大于0.5的分类器)。
而我们希望分类器达到的效果是:对于真实类别为1的样本,分类器预测为1的概率(即TPRate),要大于真实类别为0而预测类别为1的概率(即FPRate),即y >x,因此大部分的ROC曲线长成下面这个样子:
这篇关于AUC 随机抽取一个阳性样本和一个阴性样本,分类器正确判断阳性样本的值高于阴性样本之机率的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




