本文主要是介绍# [cs231n (九)卷积神经网络 ][1],希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
cs231n (九)卷积神经网络
标签(空格分隔): 神经网络
文章目录
- [cs231n (九)卷积神经网络 ][1]
- 同类文章
- 0.回顾
- 1. 引言
- 2. 总体概述
- 3. 构建卷积网络的每个层
- 1. 卷积层
- 2. pooling池化层
- 3. 归一化层
- 4. 全连接层
- 5. 全连接层转化为卷积层
- 4. 如何构建卷积神经网络的结构
- 1. 层的排列方式
- 2. 层的大小设置规律
- 3. 相关案例学习(LeNet/ AlexNet/ ZFNet/ GoogLeNet/ VGG)
- 4. 一些计算上的考虑
- 6. 其他资源
- 转载和疑问声明
- 我祝各位帅哥,和美女,你们永远十八岁,嗨嘿嘿~~~
同类文章
cs231n (一)图像分类识别讲了KNN
cs231n (二)讲了线性分类器:SVM和SoftMax
cs231n (三)优化问题及方法
cs231n (四)反向传播
cs231n (五)神经网络 part 1:构建架构
cs231n (六)神经网络 part 2:传入数据和损失
cs231n (七)神经网络 part 3 : 学习和评估
cs231n (八)神经网络总结:最小网络案例研究
cs231n (九)卷积神经网络
0.回顾
cs231n (一)图像分类识别讲了KNN
cs231n (二)讲了线性分类器:SVM和SoftMax
cs231n (三)优化问题及方法
cs231n (四)反向传播
cs231n (五)神经网络 part 1:构建架构
cs231n (六)神经网络 part 2:传入数据和损失
cs231n (七)神经网络 part 3 : 学习和评估
cs231n (八)神经网络总结:最小网络案例研究
1. 引言
经过一系列的学习终于抵达了传说中的卷积神经网络,他和一般的网络很类似,前面学过的东西这里全都能用上,那么有什么不同呢?
ConvNet结构假设输入是图像,这就允许我们将某些属性编码到体系结构中,来吧,一般究竟哈?~~~emmmm
2. 总体概述
总体结构就是:输入向量————>隐含层非线性变换————>输出
对于前面讲过的,CIFAR-10数据是32x32x3=3072(权重数), 如果图像很大呢,比如一般图像的尺寸都达到了1000x1000x3 = 3000000(权重),这时候:
计算机说:我不干了,累死我算了
卷积网络中的神经元是三维排列的,卷积只与前一层的部分连接,那么对于DIFAR数据最后一层应该是1x1x10。
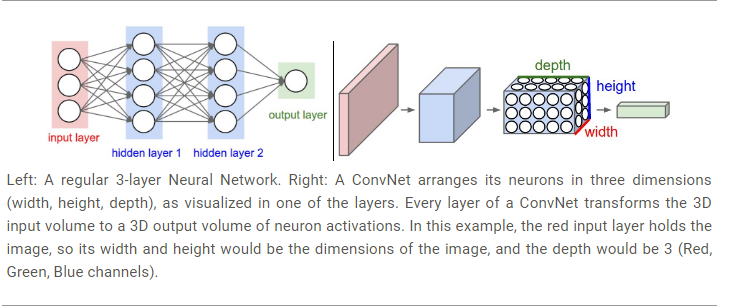
左边:三层神经网络 右边:卷积神经网络
卷积神经网络由层组成, 每层都有相应的API,用一些可导函数把输入的3D数据转换为输出的3D数据。
3. 构建卷积网络的每个层
主要由三层组成:卷积——————池化——————全连接层!
比如CIFAR数据的话:
输入层-————卷积层-————ReLU层(尺寸不变-———池化层-———全连接层
32x32x3————32x32x12——————32x32x12————————16x16x12————————1x1x10
- 输入数据变为——————输出数据
- CNN由很多层一般包含上述几种层
- 每层输入是3D数据,然后使用可导函数把它变为3D输出数据
- 有的层含参数,有的没有(卷积层和全连接层有,ReLU层和池化层没)
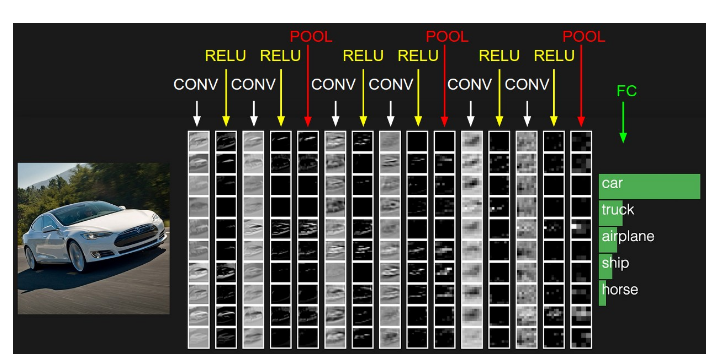
上图中的结构是一个小型VGG网络
1. 卷积层
这层是核心层,主要是由一些滤波器构成,现在使用一套滤波器(比如12个), 每层都会产生一个图数据,然后叠加就是此层的输出。
**例如:**输入数据体尺寸[32x32x3](比如CIFAR-10的RGB图像),卷积核大小是5x5,那么卷积层中的每个神经元会有输入数据体中[5x5x3]区域的权重,共5x5x3=75个权重(还要加一个偏差参数)。注意这个连接在深度维度上的大小必须为3,和输入数据体的深度相同。
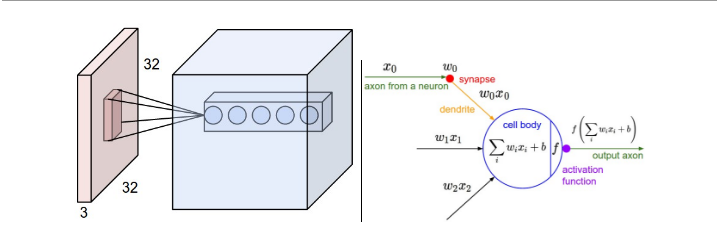
左边:输入数据,蓝色是5个卷积核叠加形成的
右边:计算的还是权重和输入的内积。
卷积层的输出: 由深度(多深),步长(一次移动多远),零填充(图像周围加零)决定。
输入数据尺寸:W 卷积核大小:F
步长:S 零填充数量:P
输出的尺寸就是: (W-F+2P)/S + 1
P取多少为好? 输入与输出相同尺寸时候满足:P=(F-1)/2
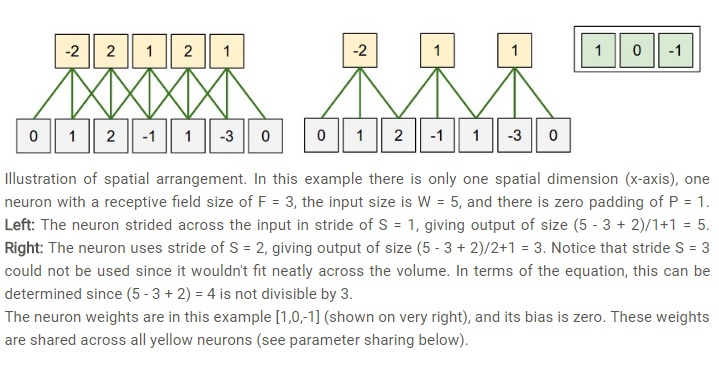
参数共享:将深度维度上一个单独的2维通道(就是一层)看做深度切片(depth slice)
比如:一个数据体尺寸为[55x55x96]的就有96个深度切片,每个尺寸为[55x55],每个深度切片上的神经元都使用同样的权重和偏差,
这样卷积层输出就有96个权重不同权重集,权重集合称为滤波器(filter),这96个滤波器的尺寸都是[11x11x3],每个都被55x55个神经元共享?

Krizhevsky等学习到的滤波器例子
具体Numpy例子
- 位于(x,y)的深度列将会是X[x,y,:]
- 位于深度d的切片应该是X[:,:,d]
假设输入数据X的尺寸X.shape:(11,11,4),不使用零填充,滤波器的尺寸:F=5,步长S=2,
输出尺寸就是(11-5)/2+1=4
- V[0,0,0] = np.sum(X[:5,:5,:] * W0) + b0
- V[1,0,0] = np.sum(X[2:7,:5,:] * W0) + b0
- V[2,0,0] = np.sum(X[4:9,:5,:] * W0) + b0
- V[3,0,0] = np.sum(X[6:11,:5,:] * W0) + b0
小结: 总结一下卷积层的性质:
输入数据体的尺寸为$ W_1\times H_1\times D_1$
4个超参数:
- 滤波器的数量K
- 滤波器的空间尺寸F
- 步长S
- 零填充数量P
输出数据体的尺寸为$W_2\times H_2\times D_2 , 其 中 : ,其中: ,其中:W_2=(W_1-F+2P)/S+1$
H 2 = ( H 1 − F + 2 P ) / S + 1 H_2=(H_1-F+2P)/S+1 H2=(H1−F+2P)/S+1 (宽度和高度的计算方法相同)
D 2 = K D_2=K D2=K
-
由于参数共享,每个滤波器包含 F ⋅ F ⋅ D 1 F\cdot F\cdot D_1 F⋅F⋅D1个权重,卷积层一共有 F ⋅ F ⋅ D 1 ⋅ K F\cdot F\cdot D_1\cdot K F⋅F⋅D1⋅K个权重和 K K K个偏置。
-
在输出数据体中,第d个深度切片(空间尺寸是 W 2 × H 2 W_2\times H_2 W2×H2),用第d个滤波器和输入数据进行有效卷积运算的结果(使用步长S),最后在加上第d个偏差。
对这些超参数,常见的设置: F=3,S=1,P=1
动态演示
输入: W 1 = 5 , H 1 = 5 , D 1 = 3 W_1=5,H_1=5,D_1=3 W1=5,H1=5,D1=3
卷积层参数: K = 2 , F = 3 , S = 2 , P = 1 K=2,F=3,S=2,P=1 K=2,F=3,S=2,P=1
输出: 是(5-3+2)/2+1=3
有2个滤波器,滤波器的尺寸是 3 ⋅ 3 3\cdot 3 3⋅3,它们的步长是2.
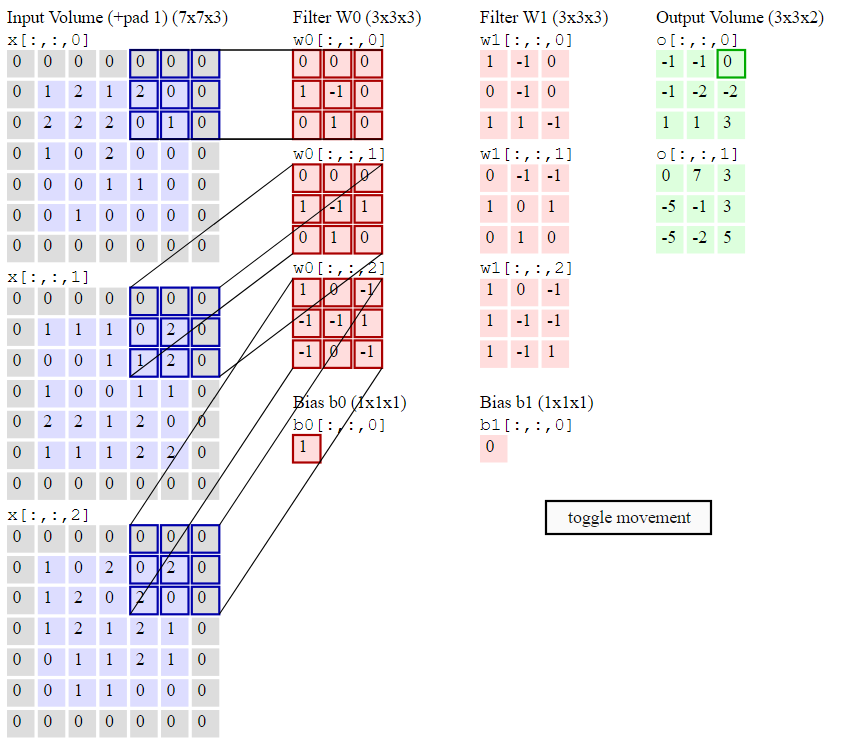
动图
1x1卷积,有意义: 因为如果我们处理的三维卷积,那么比点积更有效。
扩张卷积让滤波器中元素之间有间隙,在某维度上滤波器w的尺寸是3,
那么计算输入x的方式是: w [ 0 ] ∗ x [ 0 ] + w [ 1 ] ∗ x [ 1 ] + w [ 2 ] ∗ x [ 2 ] w[0]*x[0] + w[1]*x[1] + w[2]*x[2] w[0]∗x[0]+w[1]∗x[1]+w[2]∗x[2],此时扩张为0.
那么计算为, 如果扩张为1: w [ 0 ] ∗ x [ 0 ] + w [ 1 ] ∗ x [ 2 ] + w [ 2 ] ∗ x [ 4 ] w[0]*x[0] + w[1]*x[2] + w[2]*x[4] w[0]∗x[0]+w[1]∗x[2]+w[2]∗x[4]
2. pooling池化层
一般会在连续的卷积层之间会周期性地插入一个池化层,可以降低数据体的维度,减少参数数量,能有效控制过拟合。
输入数据体尺寸 W 1 ⋅ H 1 ⋅ D 1 W_1\cdot H_1\cdot D_1 W1⋅H1⋅D1
输出数据体尺寸 W 2 ⋅ H 2 ⋅ D 2 W_2\cdot H_2\cdot D_2 W2⋅H2⋅D2,其中
W 2 = ( W 1 − F ) / S + 1 W_2=(W_1-F)/S+1 W2=(W1−F)/S+1
H 2 = ( H 1 − F ) / S + 1 H_2=(H_1-F)/S+1 H2=(H1−F)/S+1
D 2 = D 1 D_2=D_1 D2=D1
在池化层中很少用零填充
常用参数:F = 3,S = 2; F = 2, S = 2.
有平均池化,有最大池化, L2池化等。
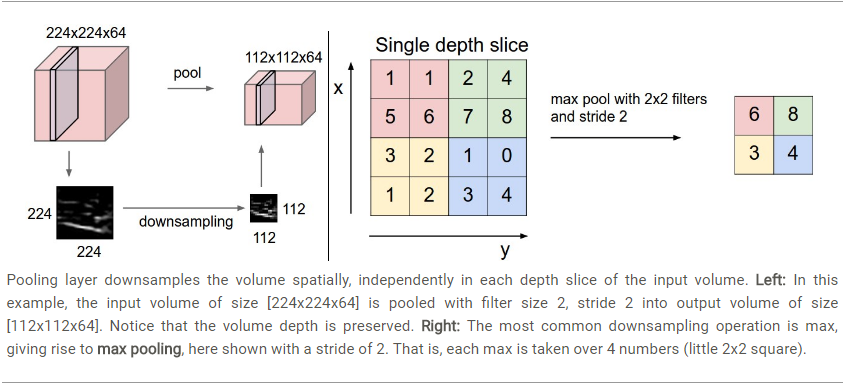
其实池化层的未来趋势就是很少使用。
3. 归一化层
归一化层几乎不用,因为他对网络性能提升很少。
4. 全连接层
神经元对前一层连接和前面学过的一般神经网络网络连接是一样的。
5. 全连接层转化为卷积层
- 卷积层和全连接层是可以相互转化的
如何转转化?
一般hi全连接层转化为卷积层更有用
输入:224x224x3
经过一系列变换
某层数据体:7x7x512
AlexNet中就是,使用5个池化层,每次尺寸下降一半,最终尺寸为224/2/2/2/2/2=7
AlexNet使用两个尺寸为4096的全连接层,最后有1000个神经元的全连接层计算分数。
这3个全连接层中的一个转化为卷积层的话:
- 对第一个连接区域 7x7x512 滤波器F=7,输出就是1x1x4096
- 对于第二层,滤波器F=1, 输出就是:1x1x4098
- 最后一个全连接层,F=1,输出就是:1x1x1000
4. 如何构建卷积神经网络的结构
那么如何组合这些,卷积层、池化层、全连接层、ReLU也算一层。
1. 层的排列方式
常见结构:**INPUT —> [[CONV -> RELU]*N -> POOL?]M -> [FC -> RELU]K —> FC
其中*N代表重复了N次,N<=3 且M>=0,K>=0,通常K<3,下面列出了常见的网络结构:
- INPUT -> FC,实现一个线性分类器,此处N = M = K = 0
- INPUT -> CONV -> RELU -> FC
- INPUT -> [CONV -> RELU -> POOL]*2 -> FC -> RELU -> FC
- INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL]*3 -> [FC -> RELU]*2 -> FC
- 上面的网络结构:在执行具有破坏性的池化前,多重的卷积可从输入中学到更多复杂特征
多个小滤波器卷积组合好于一个大滤波器
有点:输出更多的特征,且使用的特征少。
缺点:在进行反向传播时,中间的卷积层可能会导致占用更多的内存。
2. 层的大小设置规律
**输入层:**应该是可以被2整除很多次的,
3. 相关案例学习(LeNet/ AlexNet/ ZFNet/ GoogLeNet/ VGG)
4. 一些计算上的考虑
6. 其他资源
转载和疑问声明
如果你有什么疑问或者想要转载,没有允许是不能转载的哈
赞赏一下能不能转?哈哈,联系我啊,我告诉你呢 ~~
欢迎联系我哈,我会给大家慢慢解答啦~~~怎么联系我? 笨啊~ ~~ 你留言也行
你关注微信公众号1.机器学习算法工程师:2.或者扫那个二维码,后台发送 “我要找朕”,联系我也行啦!

(爱心.gif) 么么哒 ~么么哒 ~么么哒
码字不易啊啊啊,如果你觉得本文有帮助,三毛也是爱!
我祝各位帅哥,和美女,你们永远十八岁,嗨嘿嘿~~~


这篇关于# [cs231n (九)卷积神经网络 ][1]的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









