一种改进的平衡生成对抗网络用于视网膜血管分割

本文主要是介绍一种改进的平衡生成对抗网络用于视网膜血管分割，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一种改进的平衡生成对抗网络用于视网膜血管分割

Neurocomputing Volume 437, 21 May 2021, Pages 118-130

背景

视网膜血管形态学参数是眼科疾病和心血管事件早期诊断的重要指标。然而，分割性能受难以捉摸的血管的影响很大，特别是在低对比度背景和病变区域。
文中称这种难以分割的区域为：Elusive vessel segmentation，难以捉摸的血管分割

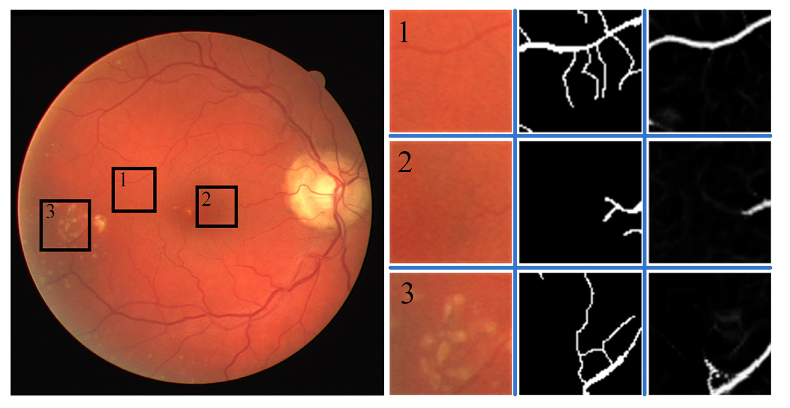
难点：

• 在难以捉摸的血管分割上表现出微弱的性能，尤其是在复杂的环境背景下。
• 在难以捉摸的血管分割中，最大的挑战是血管的口径非常小，通常为两像素或三像素的宽度。在这种情况下，该任务对细节信息提取的要求提高到了一个很高的水平

贡献

• 提出SEGAN，利用对抗原理增强G (即U - net)视网膜血管分割能力。此外，我们构建了一个对称对抗架构，该架构允许D彻底区分G的输出与真实值之间的细节差异，从而迫使G完美地伪造细节，增强了对难以捉摸血管的识别能力。
• MSFRB充分利用了浅层的高分辨率但低语义的特征。结合深层特征，设计了一个分支来跳过传统方法中出现的卷积混淆，使高分辨率信息得到很好的保留。轻量级的结构和计算保证了视网膜血管分割的高效性。
• 在MSFRB中，AM被用来为通道分配不同的权重，因此网络专注于有价值的特征通道而忽略了无价值的特征通道。此外，除了传统的GAN损失函数外，还包括两个额外的加权分割损失函数，即二进制交叉熵损失( BCE )和平均绝对误差( MAE )。优化后的目标函数更多地调整了对像素级分割任务的关注度，缓解了误判情况。

实验

• 数据集：四个公开数据集DRIVE [ 7 ]、STARE [ 33 ]、CHASEDB1 [ 34 ]和HRF [ 35 ]上完成实验，评估视网膜血管分割效果
• Evaluation metrics：
  
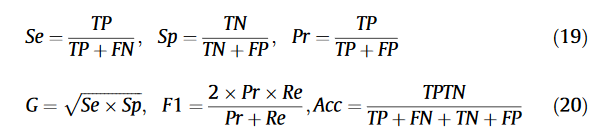
  超参数a、b、c分别（GAN、SEG_BCE、SEG_MAE）设置为0.08、1.1、0.5 (这些是我们推荐的设置,但不是最佳设置)。首先使用生成器分割血管并使用分割后的血管图和标签训练判别器，然后冻结判别器的参数并训练生成器以产生与标签高度相似的血管图。
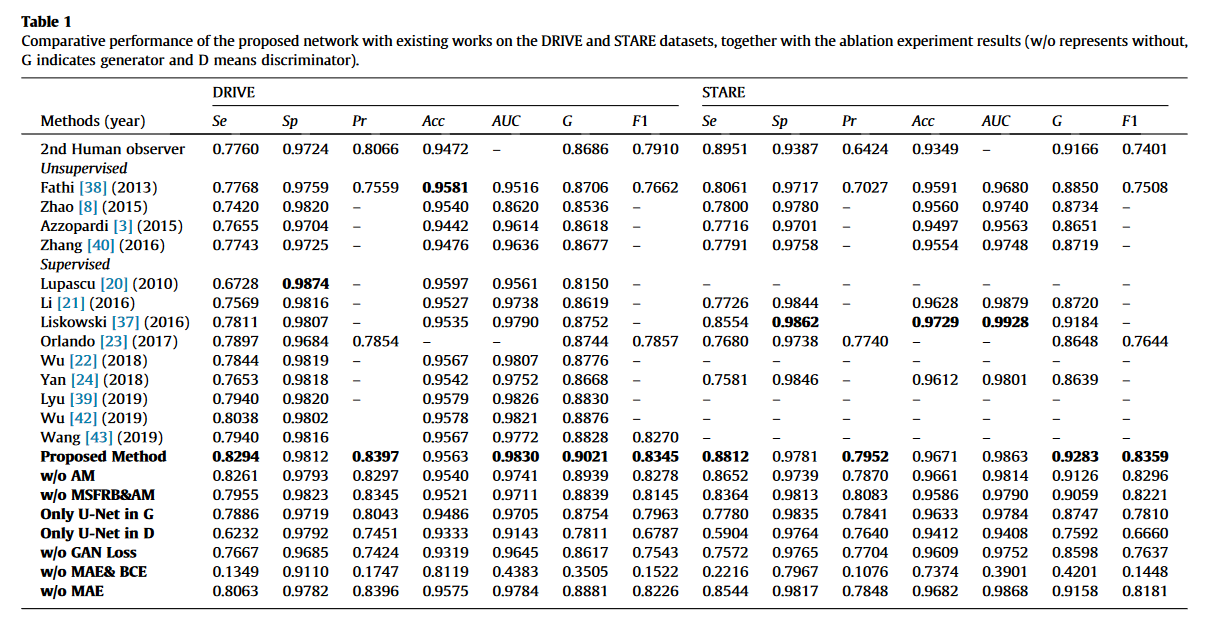
  可见，除AM模块外，都有明显的精度提升
  
  绿色越多越好，绿色表示TP，蓝色表示FP，红色表示FN。
  

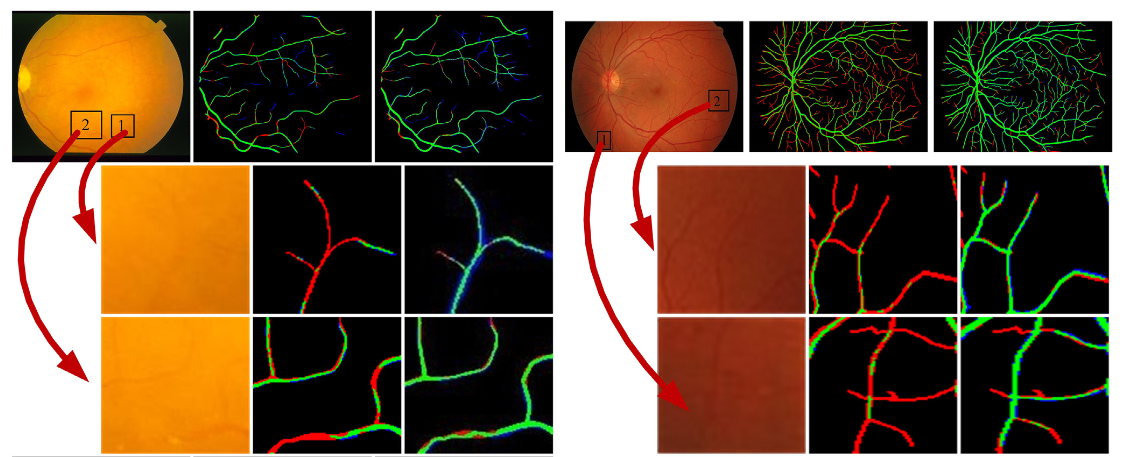
方法

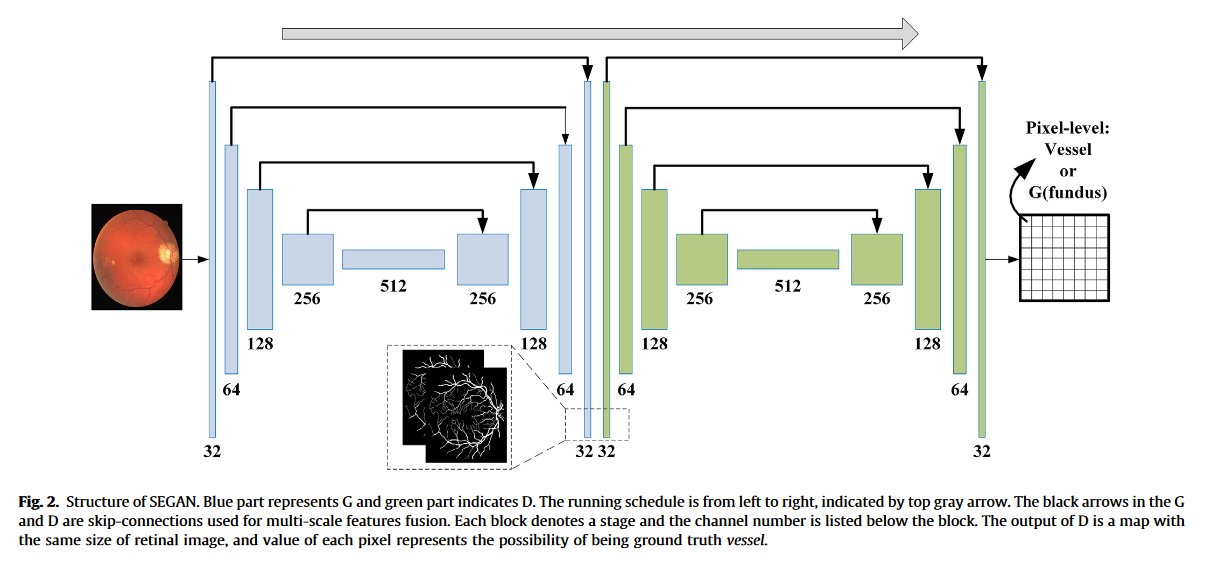
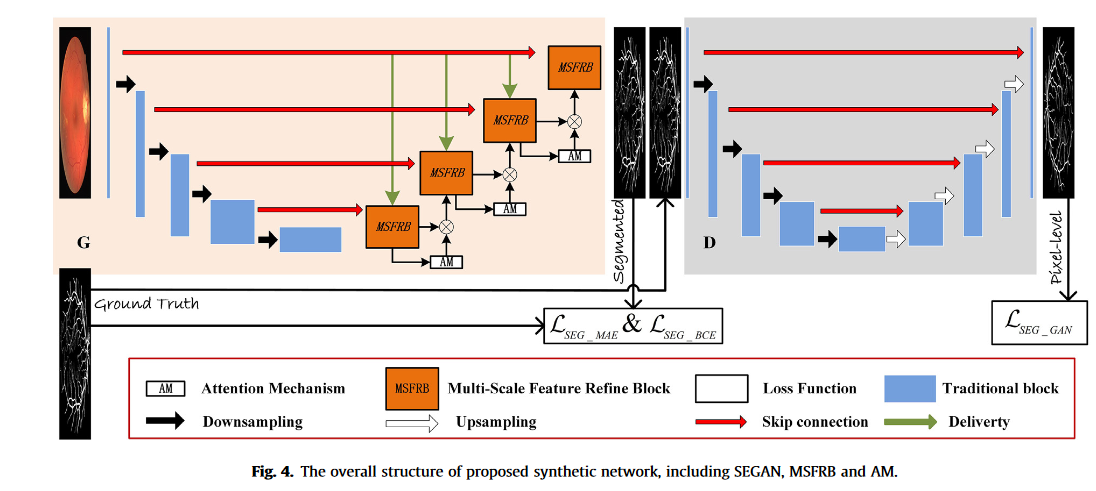
Symmetric equilibrium architecture（对称均衡架构）

使用GAN中的对抗训练来提高生成器的能力
将视网膜眼底图像作为输入，输出视网膜血管的血管概率图。然后将血管概率图与视网膜图像拼接，并输入给D进行评估。
本文提出的D的输出是一个与视网膜图像大小相同的可能性图，这意味着它区分了每个像素中的FG 和血管。这种结构赋予了D识别细节差异的能力。相应地，D重新强调了不仅有大的血管主干，还有充满细节信息的难以捉摸的血管的重要性。在这种良好匹配的设置下，加强对抗训练，以迫使G生成更真实的血管分割图。

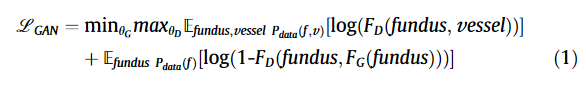
Multi-scale features refine block（多尺度特征细化模块）

MSFRB中，分支中计算的独立多尺度特征图xb s极大地保持了高分辨率特征，增强了细节信息的分割性能。同时，MSFRB在模块中引入了分辨率最高的特征xd1，使得高分辨率信息得到了很大程度的补充

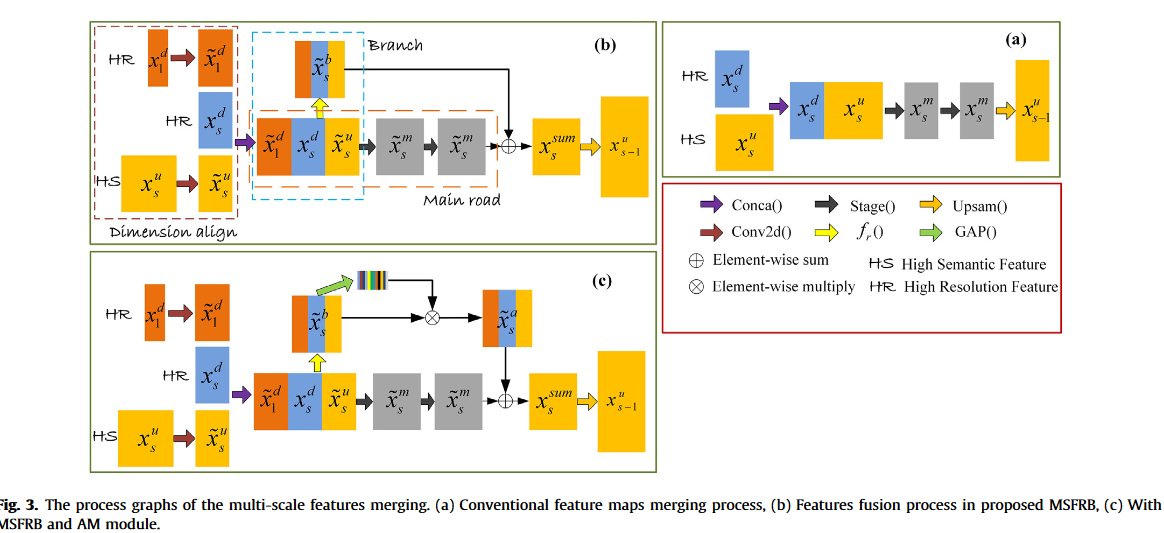
Attention mechanism

是SE模块

损失函数

GAN损失

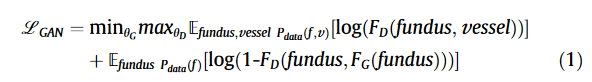
分割损失，BCE、MAE

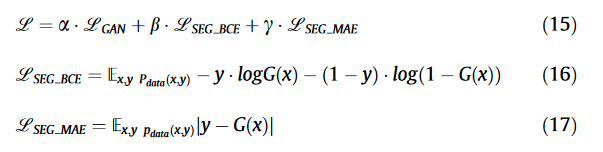
Thinking

框架新颖，虽然也对UNet进行了魔改，但是魔改UNet不是最主要的点，使用生成对抗网络分割，加权损失函数等，可能也只是为了论文好看，主要是框架新。

这篇关于一种改进的平衡生成对抗网络用于视网膜血管分割的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---