本文主要是介绍相机内参标定理论篇------张正友标定法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、为什么做相机标定?
标定是为了得到相机坐标系下的点和图像像素点的映射关系,为摄影几何、计算机视觉等应用做准备。
二、为什么需要张正友标定法?
张正友标定法使手工标定相机成为可能,使相机标定不再需要精密的设备帮助。但内参标定的精度却需要依赖采集数据的质量。精度不如专业设备的结果,不过在日常科研等对精度要求不是非常高的领域足够满足。
三、为什么张正友使手工标定相机成为可能?
我们先思考一个问题,以针孔模型为例相机标定需要那些参数:
内参:fx fy cx cy k1 k2 p1 p2;
外参:R t。
假如我们用n张图像来标定相机的话,我们需要求解8 +(3 + 3)x n = 6n + 8个参数。求解这么多参数需要使用最优化。构建目标函数:
其中为图像上角点,
为投影点。
我们知道优化问题最害怕的就是遇到局部最优,导致优化后的结果和真实值相差较大。为了解决局部最优,最好的方法是提供较为准确的初值,这就是张正友标定法最重要的作用。通过正交矩阵性质计算出不考虑畸变的相机内参和外参初值,然后利用最优化的方法,便可以得到精确的内参。
四、如何推导?
已知相机成像过程:世界坐标系->相机坐标系->相机坐标系->像素坐标系。可以用下面公式描述:

其中M为世界坐标系点,R t为世界坐标系到相机坐标系的旋转矩阵和平移量,A为相机内参矩阵,s为比例系数。
将具体数值代入公式可以获得:

其中r为R矩阵的列向量。已知世界坐标系在实际中选取为标定板坐标系,因此世界坐标系下点的Z值为零,因此可以进一步化简。
这里可以引入单应矩阵H:
![]()
用列向量表示H得:
![]()
由旋转矩阵是正交矩阵可以得到两条性质:列向量两两正交,且列向量是单位向量,因此可以得到:
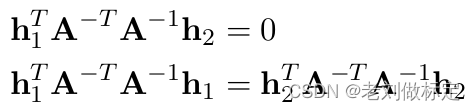
因此可以用B表示:

将B代入上式并展开得到:
![]()
其中:
![]()
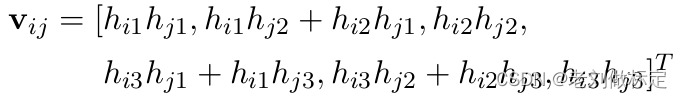
最后得到:

到现在,需要先求解H矩阵,然后利用H矩阵求解B矩阵。已知H矩阵有八个未知数(约去比例系数,使矩阵最后一项为1),利用下面公式,一对对应点可以提供两个约束,因此需要四个点可以求出单应矩阵H;
有了H矩阵值后可以得到值,已知B是对称矩阵因此有六个未知数,每个单应矩阵H可以提供两个约束,所以求解B最少需要三个不同的单应矩阵,也就是三个不同视角的标定图像。
求出B后便可以求解内参矩阵A,再得到A后利用下面公司便可以求出外参矩阵R和t:

至此便得到了相机内参的初值和不同标定图像外参的初值,然后再利用上面提到的目标函数进行最优化得到最后标定的内参。
总结:
1.张正友标定法最重要的地方是计算出了相机内参和外参的数值解,然后作为初始值代入的优化函数,解决了局部最优化的问题,是手工标定相机内参成为可能。
2.由于相机标定数据是手工采集,因此相机内参标定的精度取决于数据质量。涉及标定板选取和采集图像的注意事项,后续文章会介绍如何采集图像。
3.由于相机内外参在投影过程具有耦合关系,所以在优化时外参结果不准确也会影响内参结果,导致重投影误差很小但是得到的相机内参误差较大。
4.在需要精确内参标定结果时推荐使用相机厂商标定结果,在专业相机内参标定时,利用机械臂抓住相机在特定位置进行采图。相机外参有非常准确的初值,在优化时可以得到非常高的内参精度。
这篇关于相机内参标定理论篇------张正友标定法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!