本文主要是介绍车道线检测End-to-end Lane Detection through Differentiable Least-Squares Fitting（论文解读），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
论文链接
https://arxiv.org/pdf/1902.00293
动机
一般的车道线检测算法分为两步，第一步进行图像分割，第二步对分割结果进行后处理。这种2-step的方法不是直接预测车道线，所以通过分割的方式预测车道线不一定能够实现最佳的表现。
贡献
提出一个可以直接预测车道线的方法。利用最小二乘法可微的性质，实现车道线检测网络端到端的训练。车道线检测网络分为两个部分：（1）一个用于预测weight map的深度神经网络 （2）一个可微最小二乘法拟合模块
算法
1、输入：（1）使用一个固定转换矩阵H对RGB图片转换视角后的RGB鸟瞰图 （2）每个像素点在x轴方向坐标归一化后的x-map （3）每个像素点在y轴方向坐标归一化后的y-map
2、预测过程：（1）首先将RGB图片输入deep network获得多个weight map，每个weight map对应一条可能存在的车道线
（2）将weight maps，x-map以及y-map输入到least-squares layer，进行最小二乘法线性回归拟合训练，获得拟合各个车道线的函数的常量值，具体过程如下：
假设要检测n条车道线，则需要去拟合这条车道线获得函数常量值表示该函数。传统线性回归方法如下：
其中m是图像的分辨率，X的一行是一个车道线的x轴方向坐标值，Y的一行是一个车道线的y轴方向的坐标值。本质上这就是一个线性回归问题。把车道线视作一个连续函数曲线，能够通过求β值得到这些函数，从而在图片中准确定位车道线。通过最小二乘法，可以得到β的值：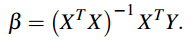
为了把图片中的上下文信息融合到车道线的定位中，本文将通过deep network提取的weight map加入车道线拟合计算中，所以对上式进行改进：
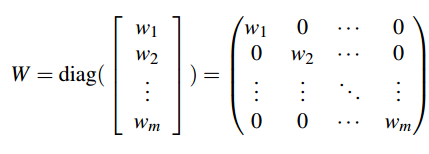
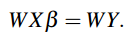加入weight map后，线性回归过程中会结合图片特征实现拟合车道线的函数的常量预测。
3、输出：拟合车道线的函数的常量值β，也就得到拟合车道线的函数曲线，即车道线定位
4、训练损失函数：最小二乘法线性回归是可微的，所以能够实现反向传播，不需要把其作为独立的后处理操作。从而可以和deep network一起训练。
一般的损失函数：
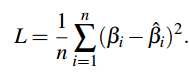
但是上述损失函数没有考虑到β向量中每个分量的敏感性。也许β中某个分量很小，但是这个分量的轻微变动就会导致最终函数曲线的巨大波动，类似蝴蝶效应。而有的分量剧烈波动但对曲线影响很小。所以考虑到β向量的各个分量的敏感性不同，重新设计了一个几何损失函数：
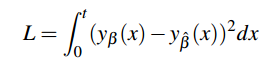
其中t是一个设置好的固定值。从积分的角度来看，其本质上就是求两个函数曲线在x∈(0,t)范围内的围成的区域在高度变为原来的平方后的面积，如下图所示。面积越大，说明越不拟合，几何损失自然也越大。
对于一次函数和二次函数，都可以求得L的积分公式，能够进行反向传播
实验
数据集
使用TuSimple数据集，并手工清除了部分车道线不清晰的图片。80%数据训练，20%数据验证。
评价指标
loss：在训练过程中几何损失函数的损失值
error：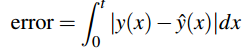
预测函数曲线和GT车道曲线在x∈(0,t)范围内的围成的区域的面积大小。
结果
cross-entropy：使用先进行语义二值分割后根据分割结果获得拟合曲线的2-step方式进行车道线检测
优缺点
优点：利用最小二乘法线性回归能够拟合曲线以及可微的性质，能够实现一步到位的端到端训练，直接预测拟合车道线的函数常量值。
缺点：deep network中的weight map固定，只能预测固定数目的车道线，无法在车道线数量变化时自适应。同时由于只用函数曲线拟合车道线，忽略了车道线的粗细情况。
总结反思
个人思考：
（1）将deep network分成两个branch输出，一个输出weight map，用于最小二乘线性线性回归，另一个用于语义分割。最后将预测的拟合车道线的函数和语义分割后的车道线进行综合，进一步通过互补纠正车道线定位，提高准确率。
（2）既然可以使用线性回归方式拟合车道线，实现车道线的定位，那么是否可以去拟合其他更加复杂的形状，从而实现图像中一些特定目标的定位？
这篇关于车道线检测End-to-end Lane Detection through Differentiable Least-Squares Fitting（论文解读）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
