本文主要是介绍开源飞控ACFLY：ADRC离散系统最速控制综合函数的理解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
摘自：https://blog.csdn.net/weixin_40767422/article/details/86709848
ACFLY原创文章，转载请说明出处https://blog.csdn.net/weixin_40767422/article/details/86709848
ADRC相关论文资料请加q群：180319060下载
最近在看韩京清教授的自抗扰论文，里面关于最速控制综合函数fhan的离散公式让我有点懵圈，于是又找到了一篇相关的论文http://www.doc88.com/p-606277652526.html，这篇论文里详细推导了离 散系统真正的最速控制综合函数 fsun()，寻思着把学习心得写一下，挺有意思的（不能让我一个人懵圈）。。。
一，先看连续化的快速最优控制系统，主要是上图中最下面那条公式，这是什么意思？其实不难，你可以把等号左边的X1看作位置，X2看作速度，那么X1求导就是X2,（X1头上加一点就代表导数），那么X2的导数自然是加速度了，这是二阶积分系统。sgn函数我就不赘述了，r代表加速度。sgn函数括号里，x1代表当前位置，V（t）代表目标位置（下图有点错），x2代表当前速度。这个公式解决的是
从一点到一点，先做匀加速运动再做匀减速运动并要求到达目标位置的速度为0，时间最短，问你什么时候应该加速什么时候应该减速。
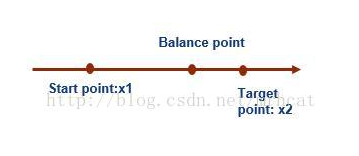
x2|x2|/2r就是初中运动公式
,指当前速度匀减速到0所需路长，x1-v(t)就是当前位置到目标位置的距离，只不过是负的，两者相加如果等于0，那么证明刚好到了平衡点，下一刻就应该减速了。大于小于0大家可以自己判断应该减速还是加速。
二,接下来重头戏看看离散化的快速最优控制系统，一堆公式。。。
1 这篇文章是相对于二阶离散系统的，我们仍然可以把x1(k)看作位置，把x(2)看作速度，h为积分步长，u(k)为控制量:加速度，u(k)<=r意思是控制量最大值为r，是人为调整的参数。离散和连续都是为了实现最速控制，所用时间最少，且到达目标位置时速度为0，即无超调，这是公式推导的基本要求，务必记住。
2.知道初始状态x1[0],x2[0]，k步之后可推导出x1[k]和x2[k]的状态,化成矩阵形式如上图（可自己动手推导验证）。系统达到稳态是指达到目标位置，到达目标位置速度x2必须为0，x1即目标位置也设为0是为了方便计算系统初始值的表达式，假设初始位置x1[0]=1，目标位置是x1=3,现在变换一下，把目标位置的点设为=0，点还是那个点，只是坐标变化一下，那么初始位置也做相应变化x1[0]=-2；式4也很容易推导，最好自己动手推导一下。为什么要得到这个式子，这个式子是k步之内达到原点(即目标位置)所有初值和控制量的关系，初值是已知的，我们要反推出最佳控制量u[k]使得k步之内无超调最快达到目标。
3.可分3种情况反推出最优控制量u[k]。这是1步之内到达原点(即目标位置)的情况，把k=1代入式4便可得出式5，有两个点a-1，a+1相当于假设一步步长为1，当初始位置在1的时候可以一步走到原点(即目标位置)，初始位置在-1的时候也可以一步走到原点(即目标位置)，只不过方向相反而已。
4.这是第二种情况，k<=2内达到原点，与上面类似，不多说，都是为了反推出最优控制量。
5.这是第3种情况，k>=3到达原点的情况。我刚开始看的时候就有一个疑问：给出最速轨迹线a后为什么还要给出轨迹b，后来我想明白了。
当我们的初始位置在最速轨迹线的时候当然最好，我们可以全速u[k]=r前进，足够靠近原点两步之内就能到达原点时，u[k]由情况2决定。
不然始终加速度最大为r，到达原点后会产生超调，就像一个人跑步，你到达终点前始终全速前进，到了终点由于速度不为0肯定还会向前移动，不符合文章开始说的无超调要求。
那当初始位置不在最速轨迹线上呢，那肯定得想方设法回到最速轨迹线上。假设初始位置在b-轨迹线的上方，要想回到最速轨迹线上，肯定得减速(这个不会看不出来吧)，而且还是以最大加速度-r减速，不然怎么符合最速控制要求呢。
如果恰好减速到b-轨迹线上最好（请看上图文字b轨迹线代表什么），再以-r减速一步便可到达最速轨迹线Gbest线上。那如果减速到a线和b线之间呢，再以-r全力减速肯定到达不了Gbest线上，这就是为什么给出b轨迹线的原因。那当系统状态变量在a线和b线之间该如何求出最佳控制量？如下图：
6式23就是所求最优控制量，可知还需求出k，k是整数，k’是为了求出k。 fix() 为取整函数. 。
至此，便可得到fsun函数的表达式。
最后总结一下，
-
当初始位置在b轨迹线上或以上或以下，控制量为|r|
-
当初始位置在a轨迹线和b轨迹线之间，想办法回到最速轨迹线
-
在最速轨迹线上，当k>=3时，控制量为|r|，当k<=2时，调整控制量使得到达原点的速度为0无超调。
这篇关于开源飞控ACFLY：ADRC离散系统最速控制综合函数的理解的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
